14.3.3 Доверительный интервал для вероятности

Доверительный интервал для вероятности. Интервал для вероятности события A в схеме независимых опытов Бернулли имеет вид

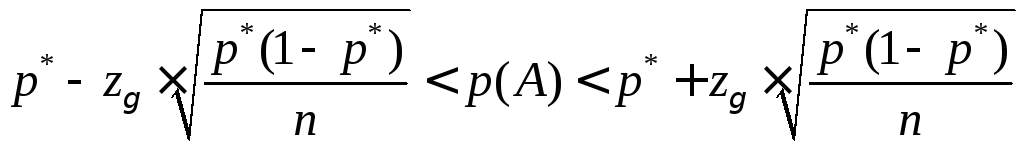, (14.25)

где – частота появления события A в n опытах;

m – число опытов, в которых произошло событие A;

n – число проведенных опытов.

–значение аргумента функции Лапласа, т.е. Ф(z_) = .

Лекция 15

15.1 Проверка статистических гипотез

Статистической гипотезой называется всякое непротиворечивое мно­жест­во утверждений {Н₀, Н₁, ¼ , H_k-1} относительно свойств распределения случайной величины. Любое из утверждений H_i называется альтернативой ги­по­тезы. Простейшей гипотезой является двухальтернативная: {H₀, H₁}. В этом случае альтернативу H₀ называют нулевой гипотезой, а H₁- конкурирующей гипотезой.

Критерием называется случайная величина ,где x_i – значения выборки, которая позволяет принять или отклонить нулевую гипотезу H₀ Значения критерия, при которых гипотеза H₀ отвергается, образуют критическую область проверяемой гипотезы, а значения критерия, при которых гипотезу принимают, область принятия гипотезы (область допустимых значений). Критические точки отделяют критическую область от области принятия гипотезы.

Ошибка первого рода состоит в том, что будет отклонена гипотеза H_0, если она верна ("пропуск цели"). Вероятность совершить ошибку первого рода обозначается  и называется уровнем значимости. Наиболее часто на практике принимают, что  = 0,05 или  = 0,01.

Ошибка второго рода заключается в том, что гипотеза H₀ принимается, если она неверна ("ложное срабатывание"). Вероятность ошибки этого рода обозначается . Вероятность не допустить ошибку второго рода (1-) называют мощностью критерия. Для нахождения мощности критерия необходимо знать плотность вероятности критерия при альтернативной гипотезе. Простые критерии с заданным уровнем значимости контролируют лишь ошибки первого рода и не учитывают мощность критерия.

15.1.1 Проверка гипотезы о равенстве вероятностей

Проверка гипотезы о равенстве вероятностей. Пусть произведено две серии опытов, состоящих соответственно из n₁ и n₂ опытов. В каждом из них регистрировалось появление одного и того же события А. В первой серии событие А появилось в k₁ опытах, во второй — в k₂ опытах, причем частота события А в первой серии получилась больше, чем во второй: 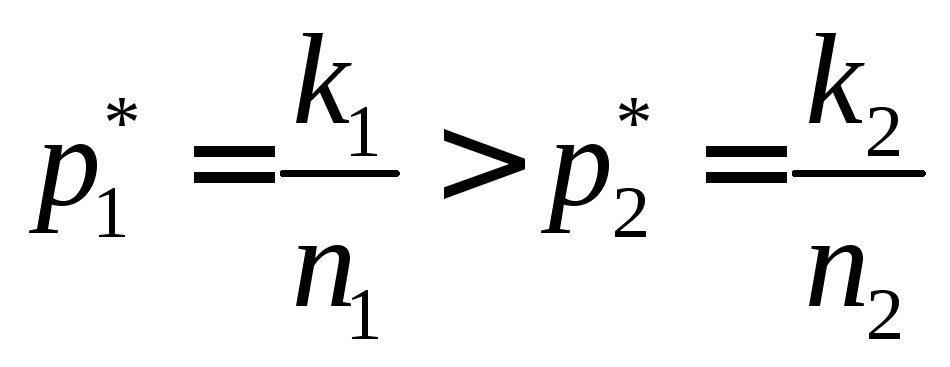. Разность между двумя частота получилась равной

. (15.1)

Спрашивается, значимо или не значимо это расхождение? Указывает ли оно на то, что в первой серии опытов событие A действительно вероятнее, чем во второй, или расхождение между частотами надо считать случайным?

Выдвинем двухальтернативную гипотезу {H₀, H₁}, где:

H₀ - различия в вероятностях не существует, т.е. обе серии опытов произведены в одинаковых условиях, а расхождение U объясняется случайными причинами,

H₁ - различие в вероятностях существует, т.е. обе серии опытов произведены не в одинаковых условиях.

В данном случае нуль-гипотеза H₀ состоит в том, что обе серии опытов однородны и что вероятность р появления события А в них одна и та же, приближенно равная частоте, которая получится, если обе серии смешать в одну:.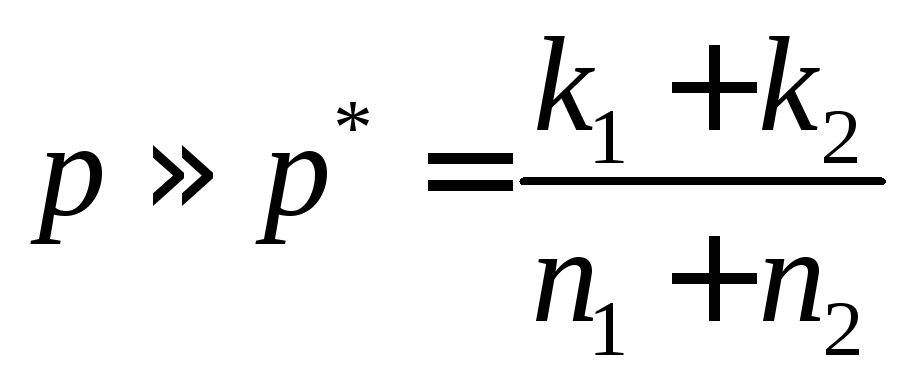

При достаточно больших n₁ и n₂ каждая из случайных величин ираспределена практически нормально, с одним и тем же математическим ожиданием. Что касается дисперсийD₁ и D₂ в первой и во второй сериях, то они различны и равны соответственно (см. (14.16))

.

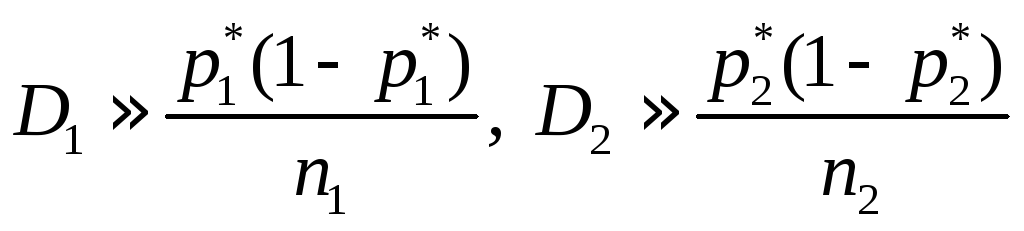В качестве критерия будем использовать случайную величину , которая также имеет приближенно нормальное распределение с математическим ожиданиеми дисперсией

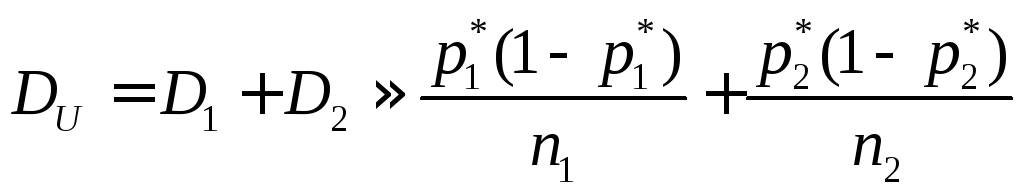, откуда .

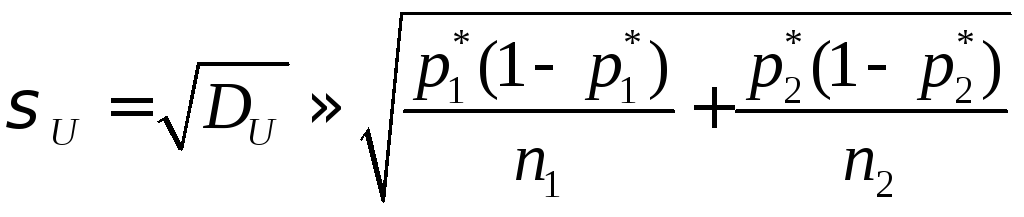Определим критическую точку U_α для заданного уровня значимости α из уравнения:

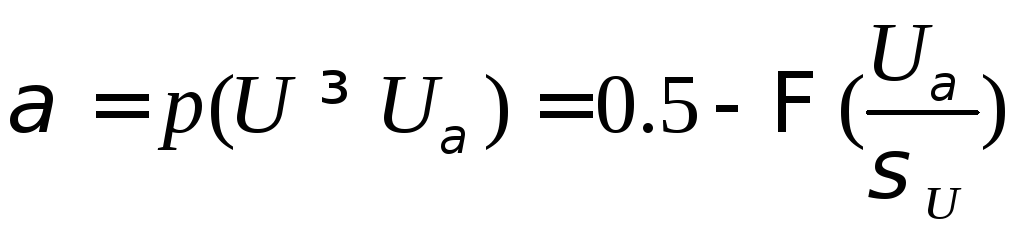т.е. .

Если значение, вычисленное по формуле (15.1), больше, чем критическое значение, т.е. , то гипотезаH₀ отклоняется, в противном случае нет оснований ее отклонить.