2.9. Поток с ограниченным последействием. Поток Пальма

Под потоком с ограниченным последействием понимается поток вызовов, у которого последовательность промежутков времени между вызовами z₁,z₂, ... представляет последовательность взаимно независимых случайных величин, имеющих любые функции распределения. Такой поток вызовов описывается последовательностью функций распределения промежутков между вызовами:

Как следует из приведенного определения потока с ограниченным последействием, свойство ограниченности последействия заключается в независимости промежутков между вызовами. Введенное ранее понятие «отсутствие последействия» потока заключается в независимости количества вызовов, поступающих в непересекающиеся отрезки времени. Таким образом, свойства «ограниченность последействия» и «отсутствие последействия» являются различными характеристиками потока.

Частным случаем потока с ограниченным последействием является рекуррентный поток, который характеризуется одинаково распределенными промежутками времени между вызовами:

Некоторым обобщением рекуррентного потока является рекуррентный поток с запаздыванием – поток с ограниченным последействием, для которого

Стационарный ординарный рекуррентный поток с запаздыванием называется потоком Пальма. Для потока Пальма, как и для любого другого стационарного ординарного потока,==1/M(Z). Распределение промежутков времени между вызовами для потока Пальма задается следующими соотношениями:

где ₀(z) – вероятность отсутствия вызовов на промежутке времени длинойz.

Весьма важной является следующая теорема Пальма (доказательство этой теоремы не приводится): если на коммутационную систему с потерями и с показательным распределением длительности обслуживания поступают вызовы, образующие поток Пальма, то поток необслуженных вызовов является также потоком Пальма. В частности, если поток поступающих вызовов будет простейшим, то поток потерянных вызовов будет потоком

Пальма. Это справедливо и для потоков, теряемых каждой линией полнодоступного пучка, работающего в режиме упорядоченного искания: если на первую линию пучка поступает поток Пальма или простейший поток вызовов, то поток потерянных вызовов любым количеством первых линий пучка будет потоком Пальма.

Простейший поток является частным случаем потока Пальма, у которого все промежутки времени между вызовами, включая первый, распределены по показательному закону. При вероятности соотношения (2.35) преобразуются к соотношению. (2.22).

Рекуррентный поток без запаздывания является ординарным потоком. Рекуррентные потоки с запаздыванием могут быть и неординарными. Доказано, что стационарный рекуррентный поток, является простейшим.

2.10. Просеивание потоков. Потоки Эрланга

Пусть имеется поток вызовов, для которого t₁,t₂,... есть моменты поступления вызовов. Выберем из этого потока часть вызовов, применив следующую операцию: вызов, поступающий в моментt_k (k=1, 2, ...), с вероятностьюостается в новом потоке и с вероятностью (1–) теряется. Новый поток вызовов называетсяпросеянным. Таким образом, просеянный поток образуется из заданного потока, в котором случайное число вызовов теряется, следующий вызов остается (просеивается), затем снова случайное число вызовов, имеющее тот же закон распределения, теряется, следующий вызов заданного потока остается и т. д. Операция, с помощью которой получен просеянный поток, называетсярекуррентной операцией просеивания. Поток, получаемый из рекуррентного потока с помощью рекуррентной операции просеивания, также является рекуррентным.

Если основной поток – простейший с параметром и каждый вызов этого потока просеивается с вероятностью р и теряется с вероятностью (1–), то просеянный поток будет также простейшим с параметром. Из этого следует весьма важный для практики вывод:если поступающий на коммутационную систему простейший поток с параметром разделяется на h направлений и вероятность того, что вызов входящего потока поступает на i-е направление (i=1,2, ...,h), равна _i,то поток i-го направления является также простейшим с параметром _i.

Используем отличную от рекуррентной операцию просеивания, при которой точно m вызовов потока теряются, (m+1)-й вызов просеивается, затем снова точно m вызовов теряются и (m+1)-й просеивается и т. д. В результате такой операции просеивания простейшего потока образуется так называемыйпоток Эрланга m-го порядка. Если в простейшем потоке сохранить (просеять) каждый третий вызов, то образуется поток Эрланга 2-го порядка, каждый второй вызов – поток Эрланга 1-го порядка. Естественно, простейший поток можно рассматривать как поток Эрланга нулевого порядка.

В потоках Эрланга любого порядка промежутки времени между вызовами независимы и распределены по одному и тому же закону, так как эти промежутки представляют собой сумму одинакового числа промежутков простейшего потока. В связи с этим потоки Эрланга являются рекуррентными.

Математическое ожидание M(Z_m), дисперсияD(Z_m) и среднеквадратическое отклонение(Z_m) промежутка времени между вызовами в потоке Эрлангаm-го порядка равны соответственно

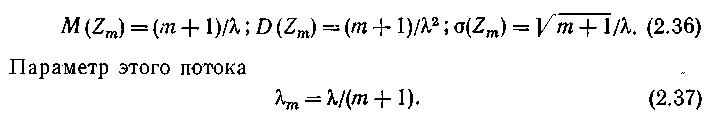
Из (2.36) и (2.37) следует, что с увеличением порядка потока Эрланга увеличиваются математическое ожидание и дисперсия промежутка времени между вызовами и одновременно уменьшается параметр потока. Потоки Эрланга m-го порядка при разныхт создают потоки с различной степенью случайности: от простейшего (m=0) до детерминированного(т=).