Колебательный		Пружинный		Физический
				контур	маятник		маятник
			I > 0				0			L
						m
	ϕ2	+	q(t)		k Fупр
								ϕ(t)
	ϕ1	- C		L
					0	x(t)	x

mg

а)

б)

в)

Рис. 1.2

Можно показать, что тогда для всех трех рассмотренных случаев имеем одно и то же дифференциальное уравнение колебательного движения

∙∙
ξ + ω02	ξ = 0 ,	(1.17)

где ω0 – частота собственных незатухающих колебаний системы (находим

из формул (1.15), (1.13), (1.16)). По формуле (1.2) можно найти период. Решением дифференциального уравнения называется функция,

обращающая это уравнение в тождество.

Нетрудно проверить прямой подстановкой, что в нашем случае решение имеет вид:

x(t) = A × cos(ω0 t + a),

(1.18)

∙∙

т. е. является гармонической функцией. Значит, уравнение ξ + ω20 ξ = 0 – это дифференциальное уравнение гармонических колебаний.

§ 4. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР. ЭНЕРГИЯ КОЛЕБАНИЙ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА

Осциллятором называют любой физический объект, совершающий колебания. Если колебания происходят по гармоническому закону, осциллятор называют гармоническим, или линейным. Например, маятники, колеблющиеся с небольшой амплитудой (пружинный, математический, физический). Если колебания происходят по негармоническому закону, осциллятор называют ангармоническим, или нелинейным. Например, маятники, колеблющиеся с большой амплитудой.

В процессе колебаний осциллятора кинетическая энергия превращается в потенциальную, а потенциальная энергия – в кинетическую.

Кинетическая энергия (см. ч. 1, (5.8)) гармонического осциллятора с учетом (1.9) и (1.13) равна:

W =	mv2		=			m	ω2A2 sin2 (ω t + α) =								kA2	sin2 (ω t + α),	(1.19)
к	2		2						0			0	2			0
где k = mω02 –							коэффициент упругой или квазиупругой силы.
Потенциальная энергия (см. ч. 1, (6.6)) гармонического осциллятора с
учетом (1.1) равна:
WП =		kx 2		=	kA 2					cos 2 (ω0 t + α).						(1.20)
	2		2
Из формул (1.19) и (1.20) следует, что полная механическая энергия:
								kA2				mω02 A	2
W = Wк + Wп =											=			.		(1.21)
									2			2

Она пропорциональна квадрату амплитуды, квадрату частоты и в процессе колебаний остается неизменной.

ИТОГИ ЛЕКЦИИ № 1

1.Колебаниями называют движения или процессы, обладающие той или иной степенью повторяемости во времени.

2.Гармоническими колебаниями называются колебания, совершающиеся по закону косинуса или синуса – (1.1) или (1.1а):

x (t) = A cos( ωt + α) или x(t) = A sin( ωt + α).

Множитель А, стоящий перед косинусом или синусом, представляет собой амплитуду колебаний. Амплитуда определяет наибольшее смещение колеблющейся величины от положения равновесия.

Аргумент косинуса или синуса представляет собой фазу колебаний. Фаза определяет смещение в данный момент времени (см. рис. 1.1).

3. Время Т одного полного колебания называется периодом. Число колебаний в единицу времени ν называется частотой. Связь между ними дается формулой (1.3):

ν= 1 .

T

Круговая частота ω вычисляется по формуле (1.5):

ω= 2πν.

4.Гармонические колебания совершаются под действием упругой или квазиупругой силы (1.11а):

F = −kx .

5. Дифференциальное уравнение гармонических колебаний составляется на основании закона движения. Для пружинного маятника оно имеет вид (1.14):

∙∙

x + ω02x = 0,

для общего случая (1.17):

∙∙

ξ + ω02ξ = 0.

Решением этих уравнений являются гармонические функции (1.1) и (1.18) соответственно.

6. Гармоническим осциллятором называют любое тело, колеблющееся по гармоническому закону. Энергия гармонического осциллятора пропорциональна квадрату амплитуды и квадрату частоты (1.21):

	W =	mω02 A2
			.
		2

ЛЕКЦИЯ № 2

Сложение колебаний

Векторная диаграмма колебания. Сложение колебаний одинаковой частоты и одного направления. Сложение колебаний близких частот.

Сложение взаимно перпендикулярных колебаний

Система может одновременно участвовать в нескольких колебаниях. Сложить два или несколько колебаний – значит, найти закон результирующего движения. В общем случае – это не простая задача, но для гармонических колебаний (1.18) возможно наглядное графическое решение – с помощью векторной диаграммы.

§ 1. ВЕКТОРНАЯ ДИАГРАММА КОЛЕБАНИЯ

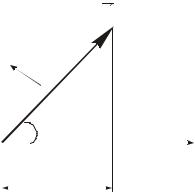
Векторная диаграмма – это способ графического задания гармонического колебательного движения в виде вектора (рис. 2.1).

Как построить векторную диаграмму?

Вдоль горизонтальной оси откладывается колеблющаяся величина ξ

(любой физической природы). Вектор A , отложенный из точки О, равен по модулю амплитуде колебания A и направлен под углом α, равным начальной фазе колебания, к оси ξ. Если привести этот вектор во вращение с угловой скоростью ω, равной циклической частоте колебаний, то угол наклона вектора к оси абсцисс равен:

ϕ = ωt + α.

Тогда проекция этого вектора на ось ξ дает значение колеблющейся величины в произвольный момент времени, т. е. меняется по гармоническому закону (1.18):

Слева на рис. 2.1 записано аналитическое задание того же колебательного движения (в виде формулы). Справа – графическое задание колебательного движения (в виде векторной диаграммы).

ϕ = ωt + α.

A

ω

			α
0			ξ(t)	ξ
x(t) = A × сos(wt + a)
	Рис. 2.1