§ 2. СЛОЖЕНИЕ КОЛЕБАНИЙ ОДИНАКОВОЙ ЧАСТОТЫ И ОДИНАКОВОГО НАПРАВЛЕНИЯ

Пусть складываются два колебания:

ξ1(t) = A1 × cos (wt + α1)

+

	ξ2 (t) = A2	× cos (wt + α2 )	.	(2.1)
	ξ(t) = A × cos (wt + α)

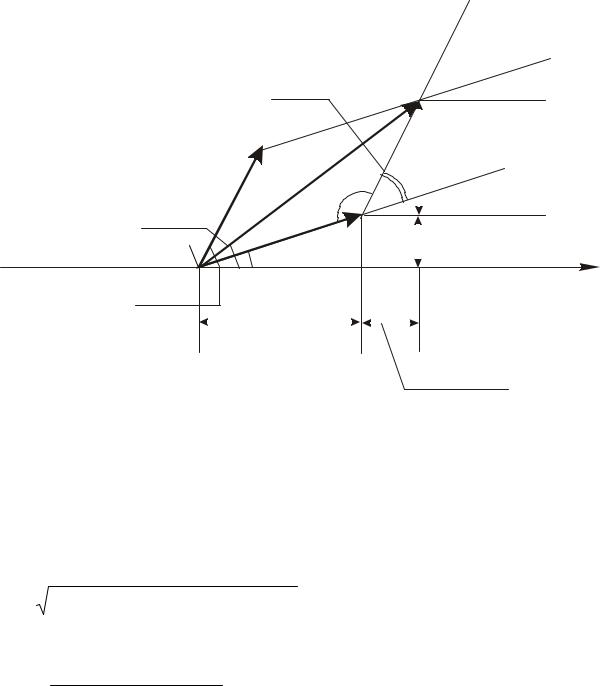
Чтобы найти А и α, строим векторные диаграммы и складываем векторы

(рис. 2.2).

	(α		− α )	+
		2	1	A = A1 A2
	A2			A2 × sin α2
α				β
				A1 × sin α1
			A1
α2	α1	× cos α1		ξ
	A1

A2 × cos α2

Рис. 2.2

По теореме косинусов

A2 = A12 + A22 - 2 × A1A2 ×cos b.

Так как b = p - (a2 - a1 ), то

A2 = A12 + A22 + 2 × A1A2 × cos (a2 - a1 ).

Амплитуда результирующего колебания равна:

A = A12 + A22 + 2A1A2 cos(a2 - a1 ) .

(2.2)

Очевидно (см. рис. 2.2), что начальная фаза результирующего колебания определяется соотношением:

tga = A1 sin α1 + A2 sin α2 . A1 cos a1 + A2 cos a2

Значит, начальная фаза результирующего колебания равна:

	A1 sin α1			+ A	2 sin α2			.	(2.3)
				+ A
α = arctg A		1	cosα		2	cosα	2
			1

Вывод: при сложении колебаний одинаковой частоты и направления результирующее колебание будет совершаться с той же частотой, что и частота складываемых колебаний. Амплитуда результирующего колебания определяется уравнением (2.2), а начальная фаза – (2.3). Как видно из (2.2), значение

амплитуды А зависит от разности фаз α2 − α1 . Если (α2 − α1 ) = 0, то

A= A1 + A 2 , если (α2– α1) = π, то A = A2 − A1 .

§3. СЛОЖЕНИЕ КОЛЕБАНИЙ ОДНОГО НАПРАВЛЕНИЯ И БЛИЗКИХ ЧАСТОТ

Пусть складывается два колебания с почти одинаковыми частотами, т. е.

ξ1(t) = A × cos wt

+

ξ2 (t) = A × cos (w + Dw)t , Δω << ω.

?

Метод векторных диаграмм позволяет проанализировать сложение колебаний близких частот на качественном уровне. Так как частоты колебаний немного различаются, то один из векторов на рис. 2.2 будет вращаться быстрее

(в нашем случае это вектор A2 ). Значит, угол между векторами A1	и A2 будет

медленно изменяться с течением времени, проходя постепенно все возможные

значения.	Следовательно, амплитуда результирующего колебания будет также
медленно	изменяться в пределах от		A1 − A2		до A1 +A2 . Это видно

непосредственно из диаграммы на рис. 2.2 и следует из формулы (2.2), в которой разность фаз α2 − α1 в нашем случае будет медленно изменяться со

временем.

Для количественного анализа сложения колебаний близких частот мы воспользуемся известной тригонометрической формулой:

cos a + cosb = 2 ×cos (α −β) ×cos (α +β) . 2 2

Применяя к нашему случаю, получим:

x = x + x				Dw			Dw		,
	2	= 2 × A ×cos			× t	×cos w+		× t
1				2			2
так как	ω << ω, то
			ω				(2.4)
ξ ≈ 2 × A × cos			2	× t × cos ωt .

График результирующего колебания – график биений, т. е. почти гармонических колебаний частоты w, амплитуда которых медленно меняется

счастотой w, представлен на рис. 2.3.

ξ(t)

Рис. 2.3

Амплитуда биений:
Aб =		2 × A × cos Dw × t		.	(2.4а)
		2
Из-за наличия знака модуля (амплитуда всегда больше нуля) частота, с
которой изменяется амплитуда, равна не					ω/ 2, а в два раза выше – Δω.

§ 4. СЛОЖЕНИЕ ВЗАИМНО-ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ

Пусть маленькое тело колеблется на взаимно-перпендикулярных пружинках одинаковой жесткости (рис. 2.4). По какой траектории будет двигаться это тело?

x(t) = A × coswt,	(2.5)
y(t) = B × cos(wt	+ a).

Это уравнения траектории в параметрическом виде.

Для получения явной зависимости между координатами x и y надо из уравнений исключить параметр t.

Из первого уравнения:

cos wt = x . A

Тогда:

2

sin ωt = ± 1− x .

A2

y

x

Рис. 2.4

Из второго уравнения:

y = B(coswt ×cosa - sinwt ×sina).

После подстановки сюда полученных выражений для coswt и sinwt получим:

y

=

x

× cosα 1 -

x 2

×sinα.

A

A

B

Избавимся от корня:

2

x

2

xy

y

2

×сos2 a - 2 ×

× сosa +

= sin2 a -

x

×sin2 a .

A

2

AB

B

2

2

A

x2

+

y2

-2×

xy

×cosa = sin2 a

–

это уравнение эллипса.

(2.6)

A2

B2

AB

Частные случаи:

1.

α = 0 ; sin α = 0 ;

cos α = 1.

x

y

2

B

y

Точка

совершает колебания

по изображенной на рис. 2.5

y

-

= 0

=

× x

прямой.

A

A

B

-A

B

x

A

-B

Рис. 2.5

y

2

B

2.

α = ±π ;

sin α = 0 ; cos α = −1;

x

+

= 0 y = -

× x .

A

A

B

На рис. 2.6 изображена траектория колеблющейся точки при значениях разности фаз a = ±p.

y

B

-A

				A	x
	-B
	Рис. 2.6
3. α = ±π/2; sinα = ±1;	cosα = 0; x2		+	y2 .
	A	2		2 = 1
				B
На рис. 2.7 изображена траектория колеблющейся точки при значениях
разности фаз α = ±π/2.
	y
Траектория – эллипс.
В зависимости от разности фаз,				α = π / 2
точка движется по часовой	B
стрелке (a=p¤2) или против
часовой стрелки (a=-p¤2)
-A				A	x
				α = −π / 2
	-B

Рис. 2.7

При сложении взаимно перпендикулярных гармонических колебаний с разными частотами результирующее движение будет происходить по сложным траекториям, называемым фигурами Лиссажу. Форма фигур Лиссажу зависит от соотношения частот складываемых колебаний и разности их начальных фаз.

Если периоды относятся как целые числа, то через промежуток времени, равный наименьшему общему кратному периодов, движущаяся точка возвращается в то же положение – получается замкнутая фигура сложной формы.