Конспект лекций Высшая математика (Басканова)

89

ГЛАВА 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

При решении геометрических задач приходится пользоваться, с одной стороны, построениями, с другой – вычислениями. Если в элементарной геометрии невозможно обойтись без построений, то аналитическая геометрия изучает геометрические объекты с помощью алгебраических методов. Основным методом аналитической геометрии является метод координат. Вза- имно-однозначное соответствие между множеством точек плоскости или пространства и множеством действительных чисел лежит в основе метода координат и позволяет геометрические задачи сводить к алгебраическим. Основные понятия аналитической геометрии находят приложение в целом ряде общетехнических и специальных дисциплин. .

ЛЕКЦИЯ 1.8. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ, ЕЕ УРАВНЕНИЯ. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ

1.8.1 Предмет аналитической геометрии

В предыдущей главе, изучая векторы, мы каждому вектору ставили в соответствие его координаты в декартовом базисе. Решая задачи с векторами, мы геометрическую задачу сводили к аналитической задаче, выясняя соотношения между координатами. Такой метод был введен Декартом и назывался методом координат. В аналитической геометрии мы будем использовать тот же подход, то есть линии и поверхности будем описывать их уравнениями, а далее изучать свойства геометрических объектов, анализируя данные уравнения.

Уравнения линий в R2 и поверхностей в R3 можно записывать как в явном, так и в неявном виде:

1. линии в R2 :

а) y = f (x) – явный вид задания;

б) F(x, y) = 0 – неявный вид задания;

2. поверхности в R3 :

а) z = f (x, y) – явный вид задания;

б) F(x, y, z) = 0 – неявный вид задания.

В данной главе мы часто будем иметь дело с геометрическим образом математического объекта, поэтому введем данное понятие. Под геометрическим образом будем понимать линию или поверхность, заданную как геометрическое место точек, обладающих общим свойством.

Пример. Составить уравнение окружности в декартовой системе координат.

90

Решение

Из школьного курса математики известно, что точки, лежащие на окружности равноудалены от центра окружности, поэтому воспользуемся данным свойством, чтобы составить ее уравнение (рис. 1.8.1)

y

y

y0 в

0 x0 x x

Рис. 1.8.1

Из рисунка определяем следующие координаты точек B(x0; y0) и M(x;y). Найдем координаты вектора ВМ , зная координаты его конца и начала:

ВМ (х х0; y y0 ) .

Для того, чтобы найти расстояние (радиус окружности) R от центра окружности B до любой текущей точки M окружности вычислим длину вектора

ВМ :

					(х х )2	( y y )2 .
R							(1.8.1)
		ВМ
					0	0

Чтобы получить уравнение окружности возведем обе части равенства (1.8.1) в квадрат и в итоге запишем каноническое уравнение окружности со смещенным центром:

(x x0 )2 ( y y0 )2 R2 .

Подводя итог данному параграфу, хотелось бы отметить, что в аналитической геометрии приходится решать два основных типа задач:

1.дана линия или поверхность как геометрическое место точек, требуется составить уравнение линии или поверхности;

2.дано уравнение линии или поверхности, требуется построить линию или поверхность.

1.8.2. Плоскость в пространстве, её уравнения. Взаимное расположение плоскостей. Расстояние от точки до плоскости

Плоскость и ее свойства изучались в курсе элементарной математики. Наша задача научиться описывать плоскость аналитически, но для этого надо знать уравнение, описывающее плоскость. Поэтому сформулируем основную теорему для плоскости.

Теорема. В декартовой системе координат любая плоскость задается линейным уравнением

91
Ax + By + Cz + D = 0	(1.8.2)
И, наоборот, любое линейное уравнение в декартовой системе коорди-

нат определяет плоскость.

Уравнение (1.8. 2) называется общим уравнением плоскости

Уравнение (1.8.2) можно записать в следующем виде:

A(x–x0) + B(y–y0) + C(z–z0) = 0 .			(1.8.3)
Уравнение (1.8.3) называется уравнением плоскости P проходящей
через точку M0(x0; y0; z0) перпендикулярно вектору	n	=(A;	B; C), который
называется нормальным вектором плоскости.

Таким образом, чтобы написать уравнение плоскости в виде (1.8.2) или (1.8.3) нужно знать координаты какой-либо точки на этой плоскости и координаты какого-либо вектора, перпендикулярного к этой плоскости.

Выведем уравнения плоскости (1.8.2) и (1.8.3).

Для этого введем в рассмотрение два вектора – это нормальный вектор плоскости n =(A; B; C) и вектор перпендикулярный данному, лежащий на плоскости М0М , причем координаты точек лежащих на плоскости P сле-

дующие: M(x; y; z), M0(x0; y0; z0) (рис. 1.8.2).

n

Р

M

M0

Рис. 1.8.2

Найдем координаты вектора

(x x0; y y0; z z0 ) .

М0М

Из условия задачи

следует, что

векторы

= (A;

B; C) и

n

(x x0; y y0; z z0 )

ортогональны между собой,

а следовательно их

М0М

скалярное произведение равно нулю:

А (х х0 ) В ( у у0 ) С(z z0 ) 0,

n

ММ0

То есть получили уравнение (1.8.3).

Раскрывая скобки в уравнении (1.8.3) и приводя подобные, имеем:

Ах Вy Сz Ах0 Вy0 Cz0 0 .

Если обозначить Ах0 Вy0 Cz0 =D,

то получим

общее

уравнение

плоскости (1.8.2):

Ax + By + Cz + D = 0.

Определение. Общее уравнение плоскости называется полным, если все его коэффициенты не равны нулю, в противном случае оно называется

неполным.

Рассмотрим различные виды неполных уравнений:

92

1.D = 0 O P;

2.A = 0 P || Ox; B = 0 P || Oy; C = 0 P || Oz;

3.A = B = 0 P Oz; A = C = 0 P Oy; B = C = 0 P Ox;

4.D = A = 0 Ox P; D = B = 0 Oy P; D = C = 0 Oz P;

5.D = A = B P xOy; D = A = C P xOz; D = B = C P yOz.

Замечание. Одна и та же плоскость может быть описана различными

уравнениями первого порядка в пространстве R3 . Выбор того или иного уравнения определяется информацией, которая известна о плоскости. Например, могут быть известны координаты трех точек плоскости или отрезки, которые отсекает плоскость от осей координат и т. п.

Запишем еще одно уравнение плоскости – уравнение плоскости, проходящей через три точки A, B, C. Пусть точка M(x; y; z) принадлежит искомой

плоскости. Тогда векторы АМ , АВ, АС будут лежать в искомой плоскости, т.е. будут компланарными. Следовательно, должно выполняться условие:

АМ АВ АС 0 . Если A(x1; y1; z1), B(x2; y2; z2), C(x3; y3; z3), то получается формула для записи уравнения плоскости, проходящей через три заданные

точки (рис. 1.8.3):

x x1 x2 x1 x3 x1

y y1 y2 y1 y3 y1

z z1

z2 z1 0 . (1.8.4) z3 z1

A

A C

M B

Рис. 1.8.3

Для построения более удобно использовать уравнение плоскости в

отрезках на осях координат:

	х		у		z	1,	(1.8.5)
	а		b		c

где a, b, c – отрезки, отсекаемые соответственно на осях Ox, Oy, Oz (рис.1.8.4)

93

z

c
	b
0	y
a

x

Рис. 1.8.4

Примеры

1. Найти уравнение плоскости, проходящей через три заданные точки:

A(1;2;0), B(2; 1; 1), C(3; 0; 1).

Решение

Подставим в уравнение (1.8.4) плоскости проходящей через три точки исходные данные. В результате вычисления данного определителя третьего порядка получим

x 1	y 2	z 0				x 1	y 2 z
2 1	1 2	1 0				1	1	1
3 1	0 2	1 0				2	2 1

(x 1) ( 1) ( y 2) 2 2 z 2z 2 (x 1) 1 ( y 2) 0

x + y – 3 = 0.

2.Составить уравнение плоскости, проходящей через точку M1 перпендику-

лярно вектору М1М2 , где M1(3; 4; 2) и M2(-1; 3; 5).

Решение

При решении данной задачи удобнее воспользоваться уравнением плоскости (1.8.3), проходящей через точку M1(3; 4; 2) перпендикулярно век-

тору М1М2 , который мы будем считать нормальным вектором плоскости. Найдем координаты нормального вектора

n = М1М2 = (-1 - 3; 3 - 4; 5 - 2) = (-4; -1; 3).

Подставляя координаты точки M1(3; 4; 2) и координаты нормального

вектора n = (-4; -1; 3) в уравнение (1.8.3), получим

-4(x – 3) -1(y – 4) + 3(z – 2) = 0

-4x + 12 – y + 4 + 3z – 6 = 0

-4x – y + 3z + 10 =0.

94

3. Дано общее уравнение плоскости 3x + 4y + 5z – 15 = 0. Привести уравнение данной плоскости к уравнению в отрезках и построить эту плоскость.

Решение

Сведем общее уравнение данной плоскости к уравнению в отрезках (1.8.5), производя элементарные арифметические преобразования:

3x + 4y + 5z – 15 = 0;									3x + 4y + 5z = 15;
	3	x		4	y		5	z 1;		x		y		z	1.
15			15			15			5			15
													3

4

Анализируя полученное уравнение в отрезках, можно заключить, что a=5, b = 154 , c = 3. Используя это уравнение легко построить плоскость по

трем точкам M1(5; 0; 0), M2(0; 154 ; 0), M3(0; 0; 3) (рис. 1.8.5).

z

3

0	15	y
5	4

x

Рис. 1.8.5

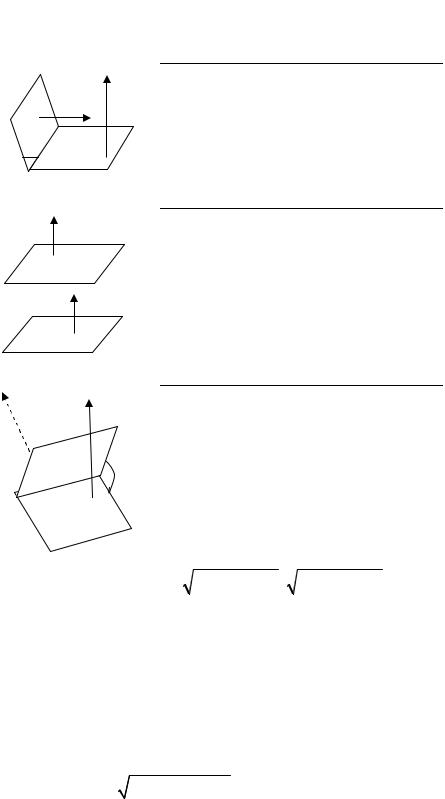
Условия параллельности и перпендикулярности плоскостей, нахождения угла между ними сводится к аналогичным задачам для нормальных векторов этих плоскостей. Удобнее проиллюстрировать взаимное расположение плоскостей в пространстве в форме табл. 1.8.1 (в таблице две плоскости заданы своими общими уравнениями: P1: A1x + B1y + C1z + D1 = 0; P2;

A2x + B2y + C2z + D2 = 0).

95

Таблица 1.8.1

Взаимное расположение плоскостей в пространстве

Случаи взаимного

Геометрическая

расположения

Формулировка условий

Интерпретация

плоскостей

n1

Плоскость P1

Так как n1

n2 , то их скалярное

n1

перпендикулярна

Р1

произведение равно нулю

1.

плоскости P2

Р2

(P1 P2)

А1 А2 В1 В2 С1 С2 0

n1

n2

n1

Так как

||

, то их координаты

n1

n2

Р1

Плоскость P1

пропорциональны

параллельна

n1

2.

плоскости P2

А

В

С

D

(P1||P2)

1

1

1

1

Р2

А2

В2

С2

D2

n2

n1

Угол между плоскостями равен углу

между их нормальными векторами

и

Плоскости P1 и P2

Р1

n1

n2

пересекаются под

n1 n2

3.

произвольным

Р2

соsα

углом

n1

n2

А1 А2 В1 В2 С1 С2

А2 В2

С2

А2

В2

С2

1

1

1

2

2

2

записать

в

нормальном виде

Уравнение

плоскости можно

xcosα y cosβ z cos γ p 0 , где cosα,cosβ,cos γ – направляющие косину-

сы нормального вектора плоскости, p>0 – расстояние от начала координат до плоскости.

Для того. чтобы перейти от общего уравнения плоскости к нормальному, его нужно умножить на величину

	1	,
	А2 В2 С2

называемую нормирующим множителем. Знак «+» или «–» выбирается таким образом, чтобы последнее слагаемое было отрицательным.

96

Аналогично получается формула для нахождения расстояния от точки M0(x0; y0; z0) до плоскости P: Ax + By + Cz + D = 0 (рис. 1.8.6).

M0 d

М

Рис. 1.8.6

d= (M0 , P) x0 cosα y0 cosβ z0 cos γ p

или

d Ах0 Ву0 Сz0 D .

А2 В2 С2

97

ЛЕКЦИЯ 1.9. ПРЯМАЯ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ. ОСНОВНЫЕ ЗАДАЧИ НА ПРЯМУЮ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

1.9.1. Прямая на плоскости

Пусть на плоскости фиксирована некоторая декартова система координат и задана прямая линия L. Ясно, что координаты точек, лежащих на прямой, не могут быть произвольными, а должны удовлетворять определенным соотношениям. Выведем эти соотношения, т.е. найдем уравнение прямой.

Рассмотрим какой-либо ненулевой вектор n =(A; B) L (рис. 1.9.1).

y

M n M0

L

0

x

Рис. 1.9.1

Очевидно, что все другие векторы, перпендикулярные данной прямой,

будут коллинеарны вектору n . Зафиксируем на прямой какую-либо точку.M0(x0;y0). Тогда все другие точки прямой, причем только они, обладают

тем свойством, что векторы			М0М		и	n		перпендикулярны, т.е.
										0.
				М0М					n
Так как		= (x-x0; y-y0), то
	М0M
			A(x-x0) + B(y–y0) = 0.								(1.9.1)

Обозначив – Ax0–By0 = C, заключаем, что в декартовой системе координат координаты точек прямой, и только они, удовлетворяют уравнению

Ax + By + C = 0.

(1.9.2)

Таким образом, мы доказали теорему.

Теорема 1. В декартовой системе координат любая прямая линия на

плоскости задается линейным уравнением (1.9.2), причем A2 B2 0 (A, B – заданные действительные числа).

Справедливо также обратное утверждение.

Теорема 2. Каждое линейное уравнение вида (1.9.2) в декартовой системе координат на плоскости определяет прямую линию, причем

A2 B2 0 (A, B – заданные действительные числа).

Рассмотренные теоремы полностью решают вопрос об уравнении прямой на плоскости. Уравнение вида (1.9.2), или ему эквивалентное (1.9.1), на-

зывается общим уравнением прямой.

98

Геометрический смысл общего уравнения прямой заключается в том, что оно описывает прямую, проходящую через точку M0(x0; y0) перпендику-

лярно вектору n = (A; B), который называется нормальным вектором прямой:

M0(x0,y0) L n =(A; B).

Определение. Общее уравнение прямой называется полным, если все его коэффициенты A, B и C отличны от нуля. Если хотя бы один из них равен нулю, то уравнение называется неполным. Рассмотрим все возможные виды

неполных уравнений:
1) C = 0 O L;	2) A = 0 L || Ox;	3) B = 0 L || Oy;

4) A = C = 0 L Ox; 5) B = C = 0 L Oy.

Для полного исследования прямых вполне достаточно использовать общее уравнение прямой. Однако прямая – это один из наиболее простых геометрических объектов. Поэтому прямая в той или иной форме встречается в различных задачах науки и техники. Особенно если учесть, что между прямыми и линейными уравнениями существует взаимно однозначное соответствие. В связи с этим большое значение приобретает разработка наиболее эффективных методов решения задач, в которых используется понятие прямой. С этой целью вводятся различные формы уравнений прямой.

Уравнение прямой с угловым коэффициентом. Если в общем уравне-

нии прямой B 0, то его можно привести к виду, которое обычно изучается в школьном курсе математики:

y = kx+b,

где k = –A/B, b = –C/B. Геометрический смысл коэффициента k – это тангенс угла наклона прямой к оси Ox, т.е. k = tg , b – это отрезок, отсекаемый прямой на оси Oy.

Найдем уравнение прямой, проходящей через точку M0(x0; y0) в направлении, определяемой угловым коэффициентом k. Поскольку M0 L, то ее координаты должны удовлетворять уравнению, т.е.

y0 = kx0+b.

Вычтем это уравнение из основного уравнения, в результате получим

y – y0 = k (x – x0).

Каноническое уравнение прямой. Поставим задачу: найти уравнение

прямой, проходящей через точку M0(x0; y0) и параллельной вектору s =(l; m). Очевидно, что такая прямая однозначно определяется точкой M0 и вектором

s . Точка M(x; y) лежит на указанной прямой тогда и только тогда, когда векторы М0M и s коллинеарны, т.е. координаты этих векторов пропорциональ-

ны (рис.1.9.2):

x x0		y y0	.	(1.9.3)
l
		m