Конспект лекций Высшая математика (Басканова)

79

Решение

По формуле (1.6.8) имеем:

								2	1	1
								1	3	1
	a		b		c
								1	1	4

2 3 4 ( 1) ( 1) 1 1 1 ( 1) 1 3 ( 1) 1 ( 1) 2 1 ( 1) 4

24 1 1 3 2 4 33.

Геометрический смысл смешанного произведения. Геометрический смысл смешанного произведения векторов a , b и c заключается в том, что

модуль смешанного произведения | a b c | равен площади параллелепипеда, построенного на этих векторах (рис. 1.6.6), то есть

a b c Vпарал-да .

c

b

a

1

Рис. 1.6.6

Замечание:

V

a

b

c

6

пирам ды

Примеры

1. Найти высоту параллелепипеда, построенного на векторах a 3i 2 j 5k , b i j 4k , c i 3 j k , если за основание взят параллелограмм, постро-

енный на векторах a и b (рис. 1.6.6).

Решение

Из стереометрии знаем, что

Vпарал-да Sосн H , H VS .

Объем параллелепипеда и площадь параллелограмма

V a b c , S a b .

Находим векторное произведение векторов a и b

80

						i			j					k															2	5						3	5						3 2
					3			2				5																																					3		17
	a		b																				i											j						k										i		j
					1			1			4																		1 4							1	4							1 1
Находим длину найденного вектора
																														32 ( 17) 2 ( 5)2													323 ,
															a							b
тогда площадь параллелограмма равна																																					323 .
Находим смешанное произведение векторов																																									,				и
																																							a					b		c
																												3		2	5			49 Vпарал-да 49 .
																												1		1	4
											a		b							c
																												1		3	1

Находим высоту

H V		49		49 323 .
S		323		323

2. Вычислить объем пирамиды с вершинами в точках О(0;

А(5;2;0), В(2; 5; 0), С(1; 2; 4) (рис. 1.6.7).

5k.

0; 0),

														O
										A												C
														B
Решение										Рис. 1.6.7
Объем пирамиды вычислим по формуле
								V						1																.
																	OA						OC				OB
								пирамиды					6
Найдем смешанное произведение векторов
								5	2	0			4 ( 1)6												5		2
																													4 (25 4) 84,
								2	5	0
	OA		OC		OB
								1	2	4															2		5
тогда														1										84
								V											84								14 .
								пирамиды					6											6				следует необходимое и
Из определения смешанного														произведения

достаточное условие компланарности векторов. Для того, чтобы три век-

81

тора а, b и c были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю, т.е.

a

b

c

=0.

(1.6.9)

Это хорошо согласуется с тем, что объем параллелепипеда, построенного на компланарных векторах, равен нулю.

Пример

Показать, что векторы

a 2i 5 j 7k , b i j k , c i 2 j 2k

компланарны.

Решение

Условие компланарности – формула (1.6.9): a b c =0. Находим смешанное произведение векторов:

2 5 7

					1	1	1 0 векторы	a	,	b	и		компланарны.
a		b		c								c
1						2	2

1.6.4. Применение элементов векторной алгебры в прикладных задачах

Рассмотрим задачу, которая наглядно демонстрирует целесообразность использования математического аппарата раздела векторной алгебры при решении задач горно-геологического направления.

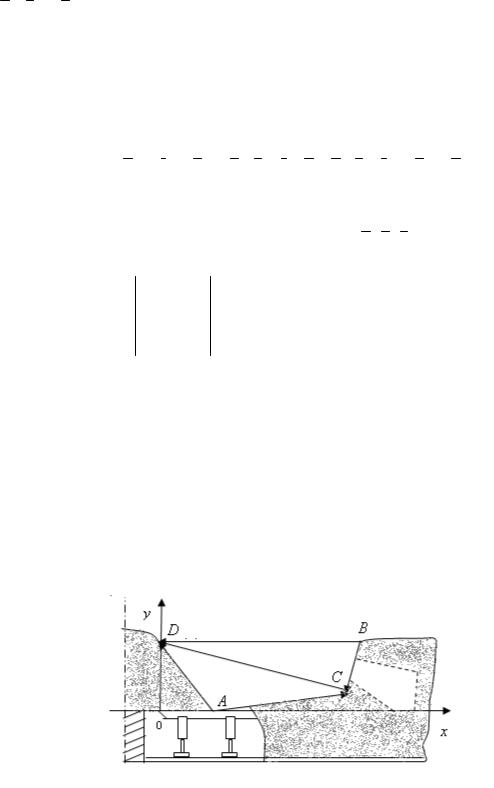
Задача. Длина породного блока одиночного слоя 15 м. Определить вес блока, если сечение блока представляет собой четырехугольник с вершинами

А(2 м; 0 м), В(10 м; 4 м), С(8 м; 2 м), D(0 м; 5 м) (рис. 1.6.8), объемная плот-

ность пород = 2,2 т/м3.

Рис. 1.6.8

Решение

Вес блока равен произведению объема на плотность пород Р = V . Объем блока равен произведению площади поперечного сечения блока и длины l , то есть V=Sсечl .

82

Для нахождения площади сечения Sсеч введем в рассмотрение векторы АD, AC, ВD, ВC Тогда Sсеч= S АDС+S ВСD . Зная координаты конца и начала соответствующих векторов, найдем координаты векторов АD, АС, ВD, ВС:

АD = (0– 2)i +(5– 0) j = – 2i +5 j ; АС = (8– 2)i +(2– 0) j = 6i +2 j ; ВD = (0– 10)i +(5– 4) j = – 10i +1 j ;

ВС= (8– 10)i +(2– 4) j = – 2i – 2 j .

Площадь треугольника АВС равна половине площади параллелограм-

ма, построенного на векторах АD =(– 2; 5) и АС = (6; 2) и выражается через модуль векторного произведения следующим образом

								S АDС =											1									.
																					АD			АС
																			2
Используя формулу вычисления векторного произведения через проек-
ции векторов на оси и формулу нахождения длины вектора, получаем:
S АDС =			1			i				j					k				1			2		5							1		34 17 м2 .
					2			5					0												k
			2																2			6		2							2
					6			2					0
Аналогично находим площадь треугольника ВСD:
S ВСD =	1			i					j					k					1			10			1									1	22 11м2 .
			10					1					0																k
	2																		2			2			2									2
			2					2					0

Тогда Sсеч= S АDС+S ВСD =17 + 11= 28 м2, а V=Sсечl =28 15 = 420 м3 .

Используя формулу нахождения веса блока, получаем

Р = V = 420 2,2 = 924 т.

83

ЛЕКЦИЯ 1.7. ЛИНЕЙНЫЕ ОПЕРАТОРЫ. МАТРИЦА ЛИНЕЙНОГО ОПЕРАТОРА. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ

Одной из фундаментальных понятий алгебры матриц – понятие линейного оператора.

Рассмотрим два линейных пространства: Rn размерности n иRm размерности m.

Если задан закон (правило), по которому каждому вектору х пространства Rn ставится в соответствие единственный вектор y пространства Rm , то

говорят, что задан оператор (преобразование, отображение) y = °(x) , дей-

A

ствующий из Rn в Rm .

Определение 1. Оператор называется линейным, если для любых векторов хи y пространства Rn и любого числа выполняются соотношения:

1.°(x y) °A(x) °A( y) – свойство аддитивности оператора;

A

2.°( x) °A(x) – свойство однородности оператора.

A

°
Вектор y = A(x) называется образом вектора х, а сам вектор х– про-
образом вектора y .							°
Если пространства	R	n	и	R	m	совпадают, то оператор
							A(x) отображает

пространство Rn в себя. Именно такие операторы мы будем рассматривать в дальнейшем.

Очевидно, что матрица, задающая линейный оператор, зависит от выбора базиса. Покажем, какова связь между матрицами, задающими в разных базисах один и тот же линейный оператор (линейное преобразование).

Пусть A и

'

°

A – матрицы одного итого же линейного оператора

A(x) в

= Х

базисах

,

,

,.......

и

e '

,

e

'

,

e

'

,.......

e '

. Тогда связь между элементом

e

e

e

e

х

1 2 3

n

1 2

3

n

°

и его образом y = Y =

A(x) в матричной форме можно записать в виде:

или

Y = AX (в старом базисе),

Y '

A' X ' (в новом базисе).

(1.7.1)

Пусть S – матрица преобразования координат при переходе к новому базису. Тогда

X SX '

Y SY ' .

Используя выше приведенные равенства, получим

Y AX Y ASX ' SY ' ASX ' Y ' S 1ASX ' .

84
Сравнивая последнее равенство с (1.7.1), получим
A' S 1AS .	(1.7.2)

Формула (1.7.2) есть формула преобразования матрицы линейного оператора при переходе к новому базису.

Матрицы A и S–1AS описывают действие одного и того же линейного

оператора ° в разных базисах. Это обстоятельство указывает на внутреннее

A

«родство» этих матриц.

Определение 2. Квадратные матрицы A иA' S 1AS (где S – невырожденная матрица) называются подобными.

Одним из важных свойств подобных матриц является равенство их определителей:

det A' = detA.

Так как матрицы одного и того же линейного оператора в разных базисах являются подобными, то из равенства определителей подобных матриц вытекает, что определитель матрицы линейного оператора не зависит от выбора базиса и, следовательно, является одной из характеристик линейного оператора (линейного преобразования).

Пример

Линейному оператору

°

соответствует матрица

A в базисе e1,e2,e3,.......en

15

11

5

20

15

8

A

.

8

7

6

°

Найти матрицу оператора

'

'

'

'

, если

A в базисе e1 ,e2

,e3

,.......en

'

2e1

3e2 e3,

e1

'

3e1

4e2 e3,

e 2

'

e1 2e2 2e3.

e 3

Решение

Матрица преобразования (оператора) координат при переходе от базиса

		,		,		,.......		к базису	e '	,	e	'	,	e	'	,.......	e	'	составленная из коэффициентов сис-
	e		e		e		e
1 2 3							n	1 2				3					n
темы имеет вид																		2		3	1
																		3		4	2
																S						.
																		1		1	2

Найдем обратную матрицу к матрице S

				85
				6		5	2
		1			4	3
		S						1 .
					1	1
								1
						°
Тогда матрица линейного оператора							в базисе		'			'		'		'		будет
						A			e1 ,e2				,e3		,.......en
иметь вид
6 5		2 15			11		5 2 3		1				1		0	0
S 1AS 4	3	1	20		15		8	3 4	2			0			2	0 .
1	1	1	8		7		6	1 1	2				0		0	3

Выше мы выяснили, что подобные матрицы обладают одинаковыми определителями. Сейчас мы выясним, что подобные матрицы обладают еще одной более общей для всех них характеристикой.

Определение 3. Рассмотрим определитель

	a11	a12	K	a1n
dеt(A E)	a21	a22	K	a2n	,	(1.7.3)
	K	K	K	K
	an1	an2	K ann

который представляет собой многочлен степени n относительно и называ-

ется характеристическим многочленом матрицы A.

Покажем, что все подобные матрицы имеют один и тот же характеристический многочлен, т.е.

|A – E| = |A– E|,

если A = S–1AS, где S – невырожденная матрица. Преобразуем матрицу A – E следующим образом:

A – E = S–1A S– S–1ES = S–1(A– E)S.

Отсюда получаем, что матрицы A– E и A – E – подобные, а значит, их определители равны.

Распишем характеристический многочлен (1.7.3), обозначая через dk

коэффициенты при степенях :

det(A– E) = d0+d1 +d2 2+...+dn n.

Так как значение определителя det(A– E) не зависит от выбора базиса, то коэффициенты dk характеристического многочлена также не зависят от выбора базиса. Таким образом, коэффициенты dk представляют собой инварианты – величины, значения которых не зависят от выбора базиса. В частности, коэффициент dn–1 равен сумме диагональных элементов матрицы A. Этот инвариант называется следом матрицы A и обозначают символом trA (от англ. trace – след) или SpA (от нем. Spur – след):

trA = SpA = a11+a22+...+ann.

Определение 4. Алгебраическое уравнение n-й степени

86

det(A– E) = 0

называется характеристическим уравнением матрицы A, а его корни – характеристическим числами этой матрицы.

Поскольку все подобные матрицы имеют одно и то же характеристическое уравнение, то характеристические числа не зависят от выбора базиса, т.е. являются инвариантами.

Определение 5. Число называется собственным значением линей-

ного оператора	°
	A , если существует такой ненулевой элемент x , что
	°
				= x .					(1.7.4)
	A x

При этом элемент x называется собственным вектором линейного опера-

тора ° , соответствующий собственному числу .

A

Теорема. Для того чтобы число было собственным значением линей-

ного преобразования ° , необходимо и достаточно, чтобы это число было ха-

A

рактеристическим.

Действительно, запишем уравнение (1.7.4) в матричном виде следующим образом

(A– E)X = 0.

Это матричное уравнение эквивалентно однородной системе линейных уравнение, которая имеет нетривиальное решение X 0 тогда и только тогда, когда определитель основной матрицы системы равен нулю, т.е. det(A– E)=0. Следовательно, собственные числа являются корнями характеристического уравнения.

Вычисление собственных значений и собственных векторов имеет огромное значение в науке и технике. Например, в электрических и механических системах собственные значения отвечают собственным частотам колебаний, а собственные векторы характеризуют соответствующие моды колебаний. Знание собственных значений позволяет анализировать многие процессы, исследовать и управлять ими. Оценки величин критических нагрузок при расчете строительных конструкций также основаны на информации о собственных значениях и собственных векторах. Собственные значения и собственные векторы являются важнейшими характеристиками, отражающих существенные стороны линейных моделей.

Отметим некоторые свойства собственных векторов.

Свойство 1. Каждому собственному вектору соответствует единственное собственное значение.

Свойство 2. Все собственные векторы, соответствующие одному и тому же собственному значению, вместе с нулевым вектором, образуют линейное подпространство.

Из последнего свойства следует, что каждому собственному значению соответствует бесконечное множество собственных векторов. В частности,

				°
	если x – собственный вектор линейного преобразования
				A, то коллинеарный

87

ему вектор k x также является собственным вектором этого преобразования с тем же собственным значением.

Для нахождения собственных векторов нужно составить характеристическое уравнение det(A– E) = 0 и найти его корни, которые будут собствен-

ными значениями линейного оператора (преобразования) ° . После этого ка-

A

ждое из найденных собственных значений i следует подставить вместо в систему (A– E)X=0 и найти все ее линейно независимые решения, которые и определяют собственные векторы, соответствующие собственному значению

i.

Пример. Найти собственные (характеристические) числа собственные

векторы линейного преобразования	°
	A, заданного матрицей
	7	12	6
A 10		19	10 .
	12	24	13

Решение. Составим характеристическое уравнение

det( A E)		7	12	6
		10	19	10		0 .
		12	24	13

Расписывая определить, получим кубическое уравнение

(1– )2(1+ ) = 0,

которое имеет корни: 1= 2=1, 3= –1. Это и есть собственные числа линей-

ного преобразования ° .

A

Составим систему линейных уравнений (A– E)X=0:

(7 )x1 12x2 6x3 0,10x1 (19 )x2 10x3 0,12x1 24x2 (13 )x3 0.

Пусть =1. Тогда получим

6x1 12x2 6x3 0,10x1 20x2 10x3 0,12x1 24x2 12x3 0.

Ранг основной матрицы этой системы равен 1, т.е. система эквивалентна одному уравнению, которое имеет вид

x1–2x2+x3 = 0.

Пусть x2=с1, x3=с2, тогда x1=2с1 – с2, т.е. общее решение системы имеет

вид

88

	2c1 c2
X	c	.
	1
	c
	2

Таким образом, система имеет два линейно независимых (фундаментальных) решения, например

2	1
X1 1	и X2 0 .
0	1

Следовательно, все собственные векторы, соответствующие собственному числу =1, имеют вид

X= с1X1+с2X2,

иобразуют двумерное линейное подпространство.

Пусть = –1. Тогда получим

8x1 12x2 6x3 0,10x1 18x2 10x3 0,12x1 24x2 14x3 0.

Ранг основной матрицы этой системы равен 2. Значит, система эквивалентна двум уравнениям

4x1 6x2 3x3 0,

5x1 9x2 5x3 0.

Пусть x3=6c, тогда общее решение этой системы будет иметь вид

3c X 5c .

6c

Таким образом, система имеет только одно линейно независимое (фундаментальное) решение, например

3 X1 5 .

6

Следовательно, все собственные векторы, соответствующие собственному числу = –1 имеют вид

X = c X1

и образуют одномерное линейное подпространство.