
- •Методические аспекты моделирования в асу и классификация моделей.
- •3. Организация статистического моделирования. Метод монте - карло.
- •Имитация равномерно распределенных случайных величин на интервале [0; 1].
- •Метод обратных функций. Примеры реализации.
- •Имитация векторных случайных величин; стандартный метод
- •Имитация нормально распределенных св (одномерный и многомерный случаи)
- •Анализ методов имитации случайных величин с заданным законом распределения (одномерный и многомерный случаи)
- •Имитация редких событий
- •Оценка количества реализаций, необходимых для достижения требуемой точности в методе статистических испытаний
- •Метод монте – карло и имитационное моделирование
- •Методы понижения дисперсии и методы вычисления интегралов
- •Регенеративный метод анализа моделей
- •Метод стратифицированной выборки
- •Методология имитационного моделирования
- •3. Формулировка математической модели.
- •Типовые математические схемы сложных систем. Агрегат и его функционирование,
- •4.Пример представления смо в виде агрегата.
- •7.Системная динамика
- •17.Метод лемера и сдвиг бернулли. Детерминированный хаос
- •35.Особенности моделирования организационно – экономических систем. Активные системы.
- •23.Характеристики интегрированной среды моделирования gpss
- •23.Основы моделирования в системе gpss
- •31.Смо; классификация и решение задач с помощью имитационного моделирования
- •36.Имитационное моделирование систем управления запасами
- •6.Метод Бокса-Уилсона.
- •3. Определение запаса для движения в направлении крутого восхождения
- •7. Проводим пошаговое приращение в каждом последующем опыте величины уровня фактора, учитывая знаки коэффициентов регрессии.
- •9. Классификация случайных процессов и корреляционные функции.
- •Корреляционные функции
- •18.Имитация потоков событий и случайных векторных величин.
- •19.Понятие детерминированного хаоса и показатель Ляпунова.
- •21. Особенности моделирования организационно-экономических систем. Производственные функции.
- •27.Системы массового обслуживания; классификация и решение задач аналитическим методом.
- •28.Методы имитации дискретных случайных величин.
- •30.Задача определения давления в пласте с помощью метода Монте-Карло.
- •32. Моделирование геологического разреза.
- •Теоретическая часть. Построение имитационной модели геологического разреза
- •34.Системы управления запасами; типовые математические модели.
- •37.Агентное моделирование.
- •Причины возникновения
- •Постановка задачи
- •Реализации
- •38.Имитация экспоненциально распределенных случайных величин.
- •40.Метод композиций; имитация св, подчиненных распределению хи квадрат.
-
Метод обратных функций. Примеры реализации.
Равномерно распределенные числа можно преобразовывать в случайные числа, имеющие заданный закон распределения.
ИМЕЕТСЯ: последовательность с.в. 1, 2… , равномерно распределенных на интервале (0,1).
ЗАДАЧА: необходимо
моделировать с.в. 1,
2…
с плотностью распределения ![]() в интервале
в интервале ![]() .
.
Задача заключается в нахождении такой
зависимости ![]() (здесь
(здесь ![]() - строго монотонная и дифференцируемая
ф-я на интервале (0, 1)), для которой
плотность распределения с.в., получаемой
соотношением
- строго монотонная и дифференцируемая
ф-я на интервале (0, 1)), для которой
плотность распределения с.в., получаемой
соотношением ![]() ,
равнялась бы
,
равнялась бы ![]() .
.
Одним из наиболее распространенных
методов подобного преобразования
является МЕТОД ОБРАТНЫХ ФУНКЦИЙ,
сформулированный как: ![]() .
.
Где ![]() - ф-я, обратная
- ф-я, обратная ![]() .
.
Лемма: Если с.в.
имеет плотность распределения ![]() ,
то
,
то ![]() имеет равномерный закон распределения
на интервале [0; 1].
имеет равномерный закон распределения
на интервале [0; 1].
![]() ,
,
![]() ,
,
![]() -функция
плотности :
-функция
плотности :
![]()
Т![]() еорема:
Пусть F(x)
– это функция распределения некоторой
случайной величины ,
– случайная
величина с равномерным законом
распределения на интервале [0, 1]. Тогда
случайная величина
еорема:
Пусть F(x)
– это функция распределения некоторой
случайной величины ,
– случайная
величина с равномерным законом
распределения на интервале [0, 1]. Тогда
случайная величина ![]() , где F-1 – обратная
функция F(x),
подчиняется закону распределения F(x).
, где F-1 – обратная
функция F(x),
подчиняется закону распределения F(x).

Квантиль порядка Р одномерного распределения – это значение хр, при котором вероятность того, что х<xр равняется p. Р{x<xр }=p
ПРИМЕРЫ:
1) Имитация равномерно распределенных на интервале [а, b] случайных величин.
![]()
Функция распределения:
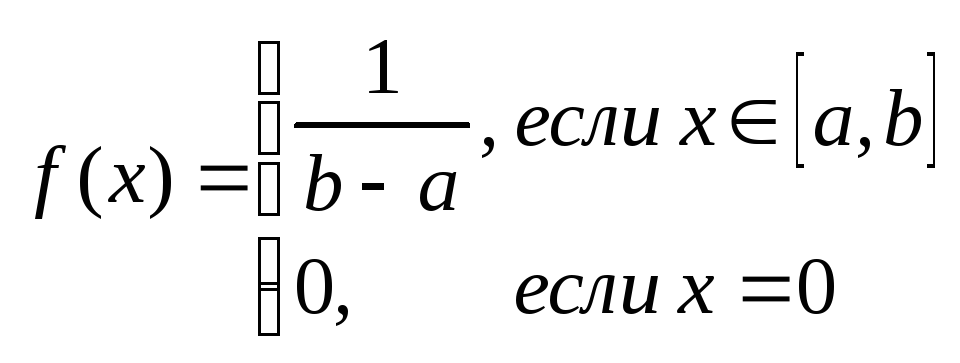
Функция плотности:
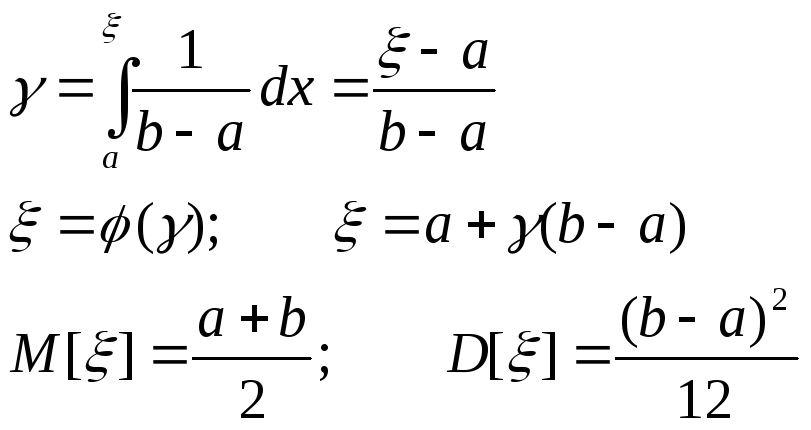
2) Имитация случайной величины ξ , которая подчиняется экспоненциальному закону распределения.
![]()
![]()
![]() Случайная величина распределена на
интервале [0, +∞].
Случайная величина распределена на
интервале [0, +∞].
![]()
![]()
![]()
![]()
Метод обратных функций применим только тогда, когда есть возможность получить квадратуру интеграла.
-
МЕТОД ИСКЛЮЧЕНИЙ (ОТБОРА).
Равномерно распределенные числа можно преобразовывать в случайные числа, имеющие заданный закон распределения.
ИМЕЕТСЯ: последовательность с.в. 1, 2… , равномерно распределенных на интервале (0,1).
ЗАДАЧА: необходимо
моделировать с.в. 1,
2… с
плотностью распределения ![]() в интервале
в интервале ![]() .
.
Задача заключается в нахождении такой
зависимости ![]() (здесь
(здесь ![]() - строго монотонная и дифференцируемая
ф-я на интервале (0, 1)), для которой
плотность распределения с.в., получаемой
соотношением
- строго монотонная и дифференцируемая
ф-я на интервале (0, 1)), для которой
плотность распределения с.в., получаемой
соотношением ![]() ,
равнялась бы
,
равнялась бы ![]() .
.
Один из приемов преобразования случайных чисел, не связанный непосредственно с решением уравнения – метод отбора. Суть метода состоит в том, что из равномерно распределенной совокупности отбираются случайные числа, удовлетворяющие некоторому условию таким образом, чтобы отобранные числа подчинялись заданному закону распределения.
Рассмотрим случайную величину ξ, определенную на интервале [а, b] с функцией плотности f(x), отграниченное сверху значением С (f(x)≤C):
Т ЕОРЕМА:
ЕОРЕМА:
Пусть γ1 и γ2 - случайные независимые числа, а
![]()
Тогда случайная величина ξ= ξ’, такая, что: η’ <f(ξ’ ), имеет функцию плотности f(x), т.е. докажем, что точки, которые попадают в подынтегральную функцию имеют функцию распределения f(x). (ξ’, η’) [a, b; 0, C].
![]()
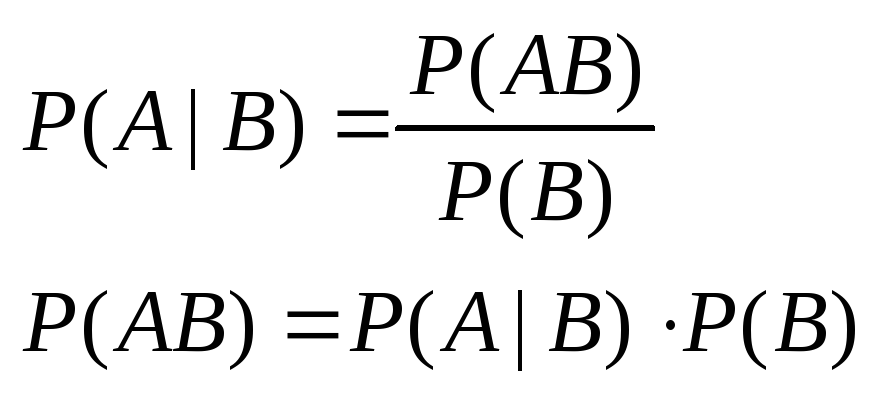
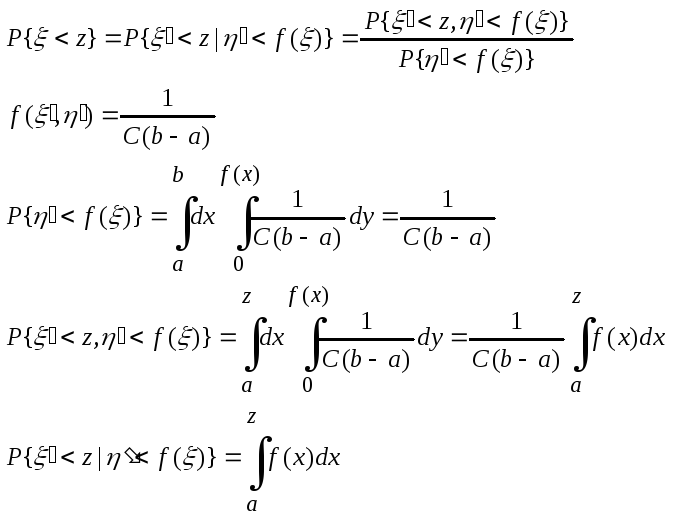
Процедура получения последовательности ξi случайных чисел, имеющих функцию плотности f(x), сводится к следующему:
-
И
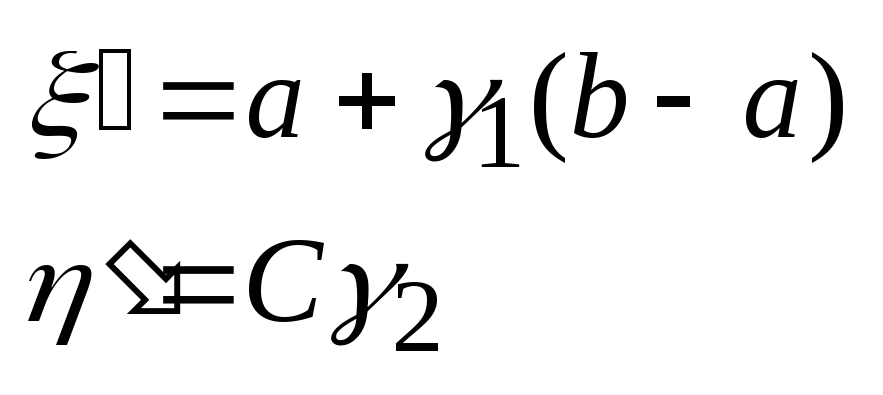 з
исходной совокупности выбираются пары
случайных независимых чисел γ1
и γ2. Находим :
з
исходной совокупности выбираются пары
случайных независимых чисел γ1
и γ2. Находим :
-
Для этих чисел проверяется справедливость неравенства:
![]()
Если неравенство верно, то ξi=ξ’i.
-
Описание процедуры отбора случайных чисел может потребовать значительного количества операций для своей машинной реализации.
-
МЕТОД КОМПОЗИЦИЙ И ПРИМЕРЫ.
Метод основан на свойствах законов распределения. Метод композиции или суперпозиции не является самостоятельным приемом моделирования непрерывных с.в., а представляет собой метод преобразования имитируемого распределения к виду, удобному для моделирования известными методами.
ПРИМЕР №1: Имитация нормально распределенных с.в.: ξ~N(μx, σx2).
Главная особенность, выделяющая нормальный закон среди других состоит в том, что это предельный закон, к которому приближаются другие законы распределения при определенных условиях.
Функция плотности вероятности f(x) случайной величины определена выражением:
![]()
Если μx
=0, σx
=1 – нормальное распределение называется
стандартным:
![]()
![]() ,
где
,
где
![]() .
Соответственно, если требуется получить
из стандартного распределения новое
нормальное с заданными значениями
среднего и стандартного отклонения, то
можно воспользоваться формулой
.
Соответственно, если требуется получить
из стандартного распределения новое
нормальное с заданными значениями
среднего и стандартного отклонения, то
можно воспользоваться формулой
![]()
Так как функция f(x) и f(y) невозможно непосредственно проинтегрировать, для получения кумулятивной функции распределения нельзя использовать метод обратных функций для моделирования случайных величин с нормальным законом распределения.
Один из методов моделирования нормально распределенных величин состоит в ПРИМЕНЕНИИ ЦЕНТРАЛЬНОЙ ПРЕДЕЛЬНОЙ ТЕОРЕМЫ (ЦПТ): Пусть с.в. X1, X2,…,Xn независимы, одинаково распределены, имеют конечные математическое ожидание МХi = μ и дисперсию DXi = σ2, i=1..n. Тогда сумма этих n с.в. будет подчинена нормальному закону распределения с МХi = nμ и DXi = nσ2.
Пусть 1,2,…,n
– равномерно распределенные числа на
интервале [0,1],тогда ![]() ,
будет подчиняться нормальному закону
распределения с МХi
= nμ
и DXi
= nσ2:
,
будет подчиняться нормальному закону
распределения с МХi
= nμ
и DXi
= nσ2:

ПРИМЕР №2: Имитация с.в, подчиненных распределению 2
Известно, что сумма квадратов ν независимых случайных величин, распределенных по нормальному закону с μx=0, σx =1 распределена по закону χ2 с ν степенями свободы: χ2(ν) = z21 + z22 + z23 + … + z2ν .
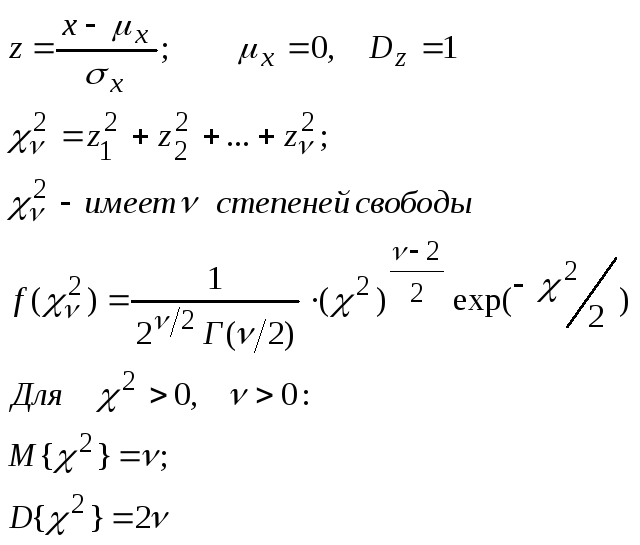

Г- гамма-функция.
На базе этих двух распределений происходит моделирование СВ, подчиненных закону t-распределения Стьюдента; СВ, подчиненных закону F-распределения Фишера-Снедекора.
