29. Методы понижения дисперсии и методы вычисления интегралов

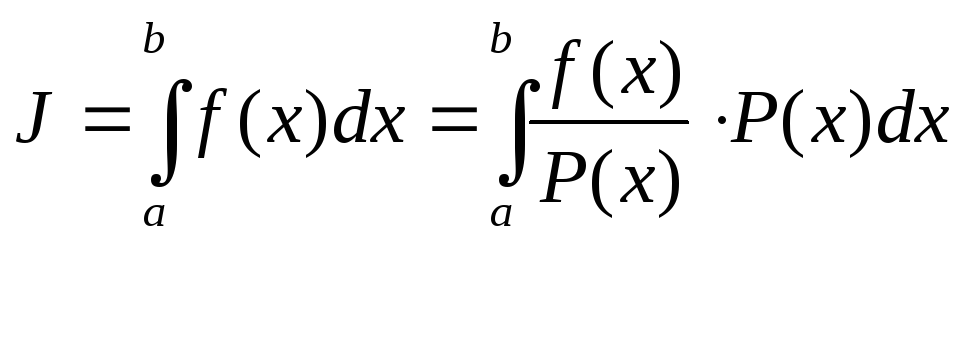
МЕТОДЫ ПОНИЖЕНИЯ ДИСПЕРСИИ ДЛЯ МЕТОДА МОНТЕ-КАРЛО. 1) Выделение главной части. 2) Существенная выборка. 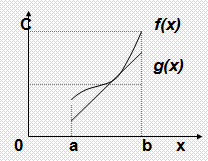l – единичная реализация

3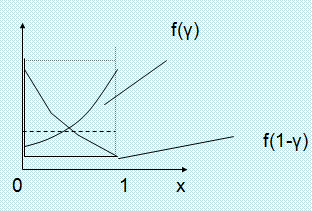) Метод симметризации подынтегральной функции.

МЕТОДЫ ПОНИЖЕНИЯ ДИСПЕРСИИ ДЛЯ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ. - Метод стратифицированной выборки (метод расслоения)[ вопрос №14] - Регенеративный метод анализа модели[ вопрос №15]

ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ. Постановка задачи: Метод Монте-Карло никогда не применяется для решения одномерных интегралов.

Методы решения.

1) Вычисление среднего значения функции. ξ - СВ равномерно распределенная на [a,b]

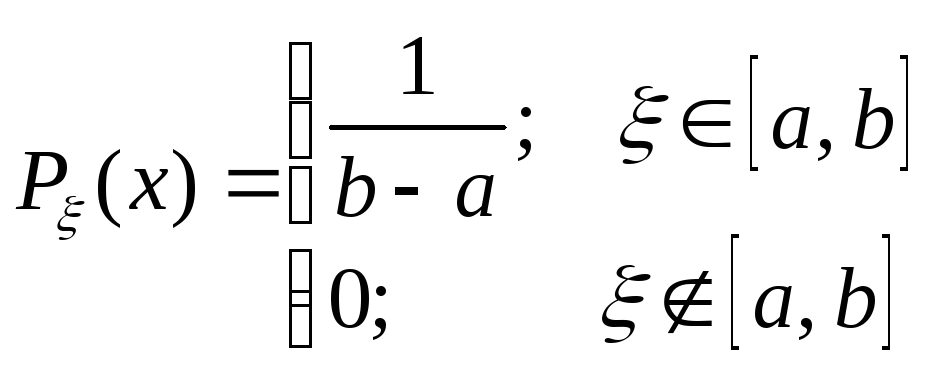
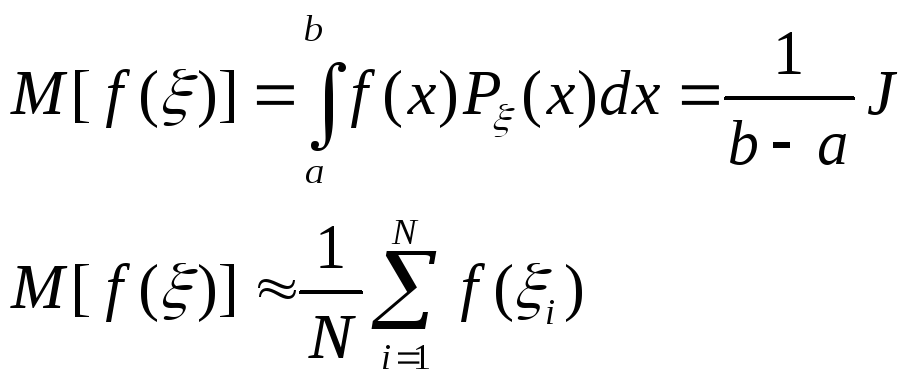
- оцениваемый параметр - оценка.

Оценка интеграла J:

2) Метод геометрической интерпретации С – максимальное значение функции

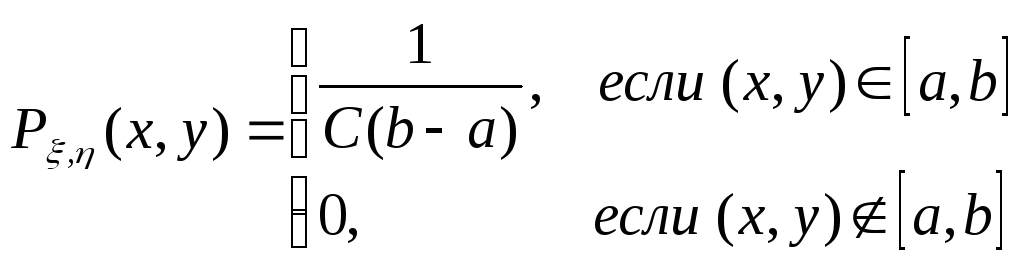
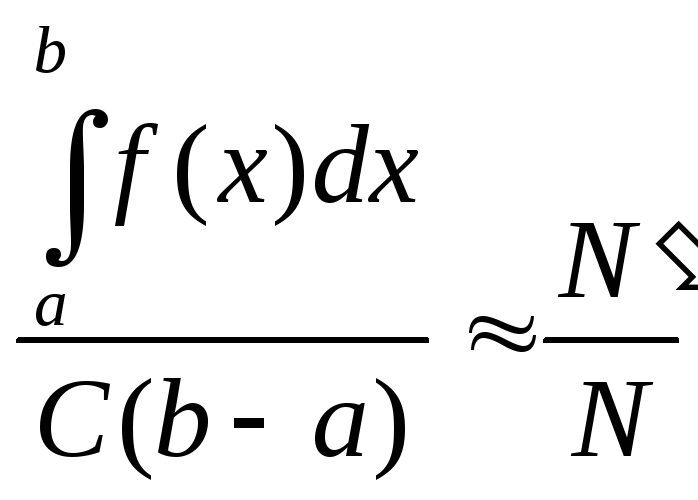
(ξ,η) двумерная точка с функцией плотности Р_ξ,η (х, у)

С(b-a) – общая площадь прямоугольника; оценка интеграла Q2:

Сравним два метода.

Имеем две оценки:

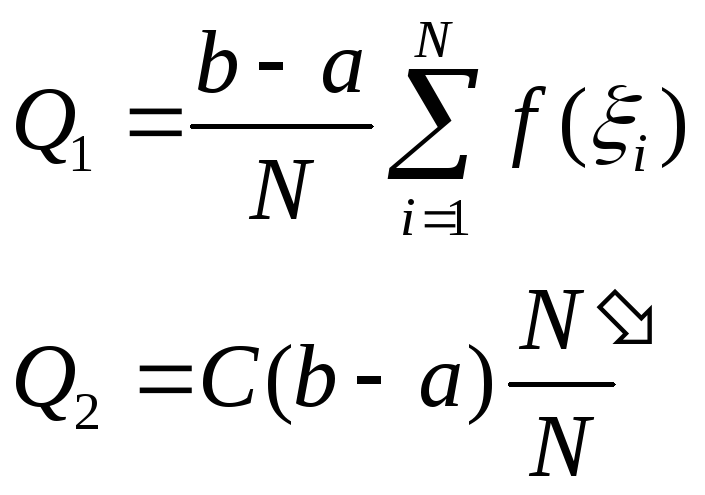
Для того, чтобы уйти от усреднения, вводим

l – единичная реализация,

DQ – дисперсия оценки.

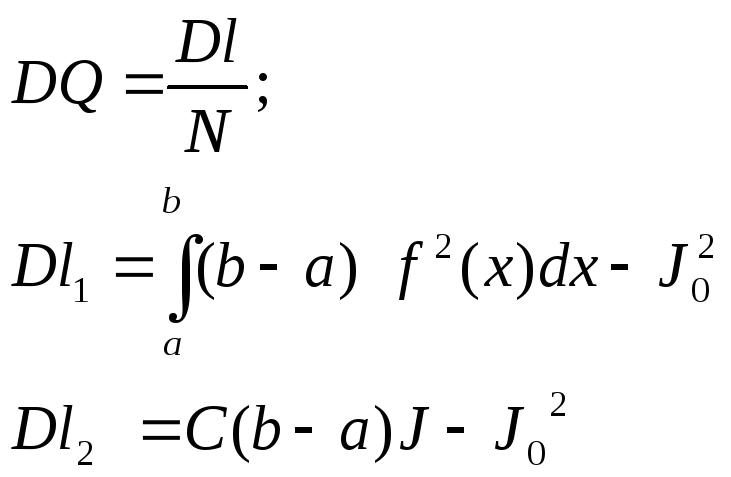
14. Регенеративный метод анализа моделей

Методы понижения дисперсии для имитационного моделирования:

- Метод стратифицированной выборки (метод расслоения)

- Регенеративный метод анализа модели

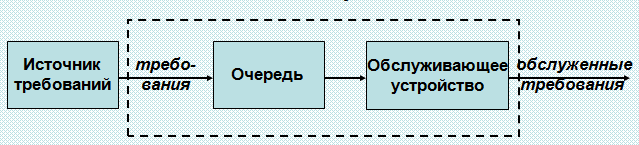
Примем за критерий качества функционирования системы E{W} – среднее время ожидания требованием (без учета времени обслуживания) в стационарном режиме.

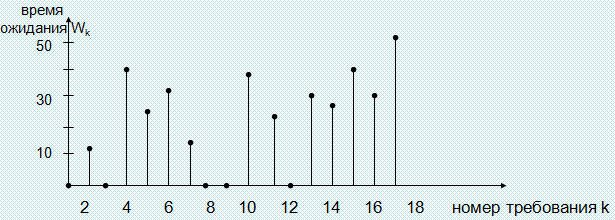
Каждый цикл начинается при одних и тех же условиях и система в эти моменты «восстанавливается», группы данных последовательных циклов статистически независимы и имеют одинаковые распределения. Итак, если положить, например, Y_k равной сумме значений длительностей ожидания на k-м цикле, а α_k – числу требований, обслуженных на k-м цикле, то пары (Y₁,α₁), (Y₂,α₂), (Y₃,α₃), (Y₄,α₄) и (Y₅,α₅) – независимые и одинаково распределенные.

Следовательно, сильно коррелированные данные {W₁, W₂….} разбились на статистически независимые и одинаково распределенные группы.

Если N – общее число требований, обслуженных на n циклах, то

и E{W} = E{Y₁}/E{α₁}.

Последовательность {X_n, n≥1} случайных векторов размерности K является регенерирующим процессом, если существует возрастающая последовательность 1≤β₁<β₂<…случайных дискретных моментов времени, называемых моментами регенерации, такая, что развитие процесса, начиная с каждого из этих моментов, определяется теми же вероятностными законами, что и в момент β₁. Это значит, что между любыми двумя последовательными моментами регенерации, например βj и βj+1, часть процесса

{X_n, βj ≤ n < βj+1}

является независимой «вероятностной копией» части процесса между любыми двумя другими последовательными моментами регенерации. Однако для части процесса, заключенного между моментом 1 и моментом β₁, хотя и независимой от остальных частей, допускается отличие от них по распределению. Часть процесса {X_n, βj ≤ n < βj+1} будем называть j-м циклом.

Любой регенерирующий процесс с дискретным временем, представляющий практический интерес, имеет в некотором смысле стационарное распределение и наиболее часто в следующем привычном значении: существует К-мерный случайный вектор Х такой, что распределение X_n сходится к распределению X при n→∞, т.е.