
- •СамарсКий государственНый университет путей сообщения
- •Содержание
- •Аналитическая геометрия
- •I. Прямые и плоскости
- •1. Плоскость
- •Задание 1
- •Задание 2
- •Задание 3
- •2. Прямая в пространстве. Прямая и плоскость
- •Задание 4
- •Задание 5
- •Задание 6
- •3. Прямая на плоскости
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Дополнительные задания
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •5 Вариант
- •6 Вариант
- •7 Вариант
- •8 Вариант
- •9 Вариант
- •10 Вариант
- •11 Вариант
- •12 Вариант
- •13 Вариант
- •14 Вариант
- •15 Вариант
- •16 Вариант
- •17 Вариант
- •18 Вариант
- •19 Вариант
- •20 Вариант
- •21 Вариант
- •22 Вариант
- •23 Вариант
- •24 Вариант
- •25 Вариант
- •26 Вариант
- •II Линии и поверхности второго порядка
- •1. Окружность и сфера
- •2. Эллипс и эллипсоид
- •3. Гипербола и гиперболоиды
- •4. Парабола и параболоиды
- •Задание 11
- •Задание 12
- •Задание 13
- •5. Цилиндры второго порядка. Конус второго порядка
- •6. Поверхности вращения
- •Задание 14
- •Задание 15
- •III. Линии, заданные уравнениями в полярных координатах и параметрическими уравнениями
- •1. Полярные координаты точки и уравнение линии в полярных координатах
- •Задание 16
- •Задание 17
- •Задание 18
- •2. Параметрические уравнения линии
- •Задание 19
1. Окружность и сфера
Определение.
Совокупность точек плоскости,
равноудаленных от данной точки
![]() (центра окружности), называется
окружностью.
(центра окружности), называется
окружностью.
Окружность
с центром в т.
![]() и радиусом
и радиусом
![]() задается уравнением (каноническим)
задается уравнением (каноническим)
![]() . (1.3)
. (1.3)
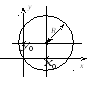
Окружность
с центром в т.
![]() и радиусом
и радиусом
![]() (на рисунке) задается уравнением
(на рисунке) задается уравнением
![]() . (1.4)
. (1.4)
В пространстве окружности соответствует сфера. Каноническое уравнение сферы:
![]() . (1.5)
. (1.5)
Если
же центр сферы находится в т.
![]() то уравнение ее имеет вид:
то уравнение ее имеет вид:
![]() (1.6)
(1.6)
2. Эллипс и эллипсоид
Определении.
Эллипсом
называется совокупность точек М
плоскости, сумма расстояний от каждой
из которых до двух данных точек (фокусов
эллипса) есть величина постоянная, т.е.
![]() .
.

Здесь
т.
![]() - фокусы эллипса;
- фокусы эллипса;
![]() - большая полуось,
- большая полуось,
![]() - малая полуось;
- малая полуось;
![]() - фокусное расстояние; прямые
- фокусное расстояние; прямые
![]() и
и
![]() - директрисы эллипса.
- директрисы эллипса.
Канонические
уравнение эллипса с центром в т.
![]() и полуосями
и полуосями
![]() и
и
![]() имеет вид:
имеет вид:
![]() . (2.1)
. (2.1)

Фокусное расстояние можно определить из соотношения:
![]() ;
;
эксцентриситет
эллипса
![]() ;
;
уравнения
директрис
![]() .
.
В
случае, если
![]() ,
то фокусное расстояние определяется
по формуле
,
то фокусное расстояние определяется
по формуле
![]() ;
эксцентриситет
;
эксцентриситет
![]() ;
уравнение директрис
;
уравнение директрис
![]() .
.
 Если
центр эллипса находится в т.
Если
центр эллипса находится в т.
![]() ,
то его уравнение имеет вид:
,
то его уравнение имеет вид:
![]() (2.2)
(2.2)
В
пространстве эллипсу соответствует
эллипсоид. Его каноническое уравнение
(центр в т.
![]() и полуоси а,
b,
с),
имеет вид:
и полуоси а,
b,
с),
имеет вид:
![]() (2.3)
(2.3)
Если
же центр эллипсоида находится в т.
![]() ,
то уравнение (2.3) преобразуется:
,
то уравнение (2.3) преобразуется:
![]() (2.4)
(2.4)
3. Гипербола и гиперболоиды
Определение.
Гиперболой
называется совокупность точек М
плоскости, абсолютная величина разности
расстояний от которых до двух данных
точек (фокусов гиперболы) есть величина
постоянная, т.е.
![]() .
.

Здесь
![]() - фокусы гиперболы,
- фокусы гиперболы,
![]() - действительная полуось,
- действительная полуось,
![]() - мнимая полуось,
- мнимая полуось,
![]() - фокусное расстояние,
- фокусное расстояние,
![]() и
и
![]() - директрисы гиперболы,
- директрисы гиперболы,
![]() и
и
![]() - асимптоты гиперболы. Каноническое
уравнение гиперболы с центром в т.
- асимптоты гиперболы. Каноническое
уравнение гиперболы с центром в т.
![]() и полуосями: действительной
и полуосями: действительной
![]() и мнимой
и мнимой
![]() имеет вид:
имеет вид:
![]() (3.1)
(3.1)
Для
гиперболы
![]() ;
;
эксцентриситет
эллипса
![]() ;
;
уравнения
директрис
![]() ;
;
уравнение
асимптот
![]() .
.
Гипербола, уравнение которой имеет вид
![]() (3.2)
(3.2)
называется сопряженной с гиперболой (3.1) и имеет вид:

Здесь
![]() - мнимая полуось,
- мнимая полуось,
![]() -действительная полуось;
-действительная полуось;
эксцентриситет
эллипса
![]() ;
;
уравнения
директрис
![]() .
.
Если
центр гиперболы смещен в т.
![]() ,
то уравнение (3.1) и (3.2) принимают вид:
,
то уравнение (3.1) и (3.2) принимают вид:
![]() (3.3)
(3.3)

![]() (3.4)
(3.4)
В пространстве гиперболе соответствуют гиперболоиды: однополостный и двухполостный.
Однополостный гиперболоид описывается уравнением
![]() (3.5)
(3.5)
и имеет вид

двухполостный гиперболоид описывается уравнением
![]() (3.6)
(3.6)
4. Парабола и параболоиды
Определение.
Параболой
называется совокупность точек М
плоскости, каждая из которых равноудалена
от данной точки (фокуса параболы) и
данной прямой (директрисы параболы)
т.е.
![]() .
.

Здесь
F
– фокус параболы, расстояние от директрисы
до фокуса
![]() - параметр параболы. Каноническое
уравнение параболы с вершиной в т.
- параметр параболы. Каноническое
уравнение параболы с вершиной в т.
![]() ,
параметром р
и ветвями, направленными вправо имеет
вид
,
параметром р
и ветвями, направленными вправо имеет
вид
![]() (4.1)
(4.1)
Уравнения
![]() ,
,
![]() ,
,
![]() определяют параболы, иначе ориентированные
относительно осей координат.
определяют параболы, иначе ориентированные
относительно осей координат.

Если
вершина параболы находится в т.
![]() ,
то ее уравнение выглядит одним из
следующих образов
,
то ее уравнение выглядит одним из
следующих образов
![]() ,
,
![]()
![]() (4.2)
(4.2)
![]()
В пространстве параболе соответствуют параболоиды: эллиптический и гиперболический.
Эллиптический параболоид описывается уравнением
![]() (4.3)
(4.3)
и имеет вид

Гиперболический параболоид описывается уравнением
![]() (4.4)
(4.4)
и имеет вид.

