Задание 9

Даны вершины треугольника : , , . Построить треугольник и найти:

1. уравнения сторон и ;

2. уравнение высоты ;

3. уравнение медианы ;

4. точку пересечения медианы и высоты ;

5. уравнение прямой, проходящей через вершину параллельно стороне ;

6. угол ;

7. длину высоты .

№ вар.				№ вар.
1	(–2;4)	(3;1)	(10;7)	2	(–3; –2)	(14;4)	(6;8)
3	(1;7)	(–3; –1)	(11; –3)	4	(1;0)	(–1;4)	(9;5)
5	(1; –2)	(7;1)	(3;7)	6	(–2; –3)	(1;6)	(6;1)
7	(–4;2)	(–6;6)	(6;2)	8	(4; –3)	(7;3)	(1;10)
9	(4; –4)	(8;2)	(3;8)	10	(–3; –3)	(5; –7)	(7;7)
11	(1; –6)	(3;4)	(–3;3)	12	(–4;2)	(8; –6)	(2;6)
13	(–5;2)	(0; –4)	(5;7)	14	(4; –4)	(6;2)	(–1;8)
15	(–3;8)	(–6;2)	(0; –5)	16	(6; –9)	(10; –1)	(–4;1)
17	(4;1)	(–3; –1)	(7; –3)	18	(–4;2)	(6; –4)	(4;10)
19	(3; –1)	(11;3)	(–6;2)	20	(–7; –2)	(–7;4)	(5; –5)
21	(–1; –4)	(9;6)	(–5;4)	22	(10; –2)	(4; –5)	(–3;1)
23	(–3; –1)	(–4; –5)	(8;1)	24	(–2; –6)	(–3;5)	(4;0)
25	(–7; –2)	(3; –8)	(–4;6)	26	(0;2)	(–7; –4)	(3;2)
27	(7;0)	(1;4)	(–8; –4)	28	(1; –3)	(0;7)	(–2;4)
29	(–5;1)	(8; –2)	(1;4)	30	(2;5)	(–3;1)	(0;4)

Задание 10

Решить следующие задачи.

1 вариант. Найти уравнение прямой, проходящей через точку пересечения прямых и отсекающей на оси абсцисс отрезок, равный 3.

2 вариант. Найти проекцию точки А (–8,12) на прямую, проходящую через точки В (2,–3) и С(–5,1).

3 вариант. Даны две вершины треугольника ABC: A (–4,4), В(4, –12) и точка М(4,2) пересечения его высот. Найти вершину С.

4 вариант. Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой

5 вариант. Найти уравнение прямой, проходящей через точку А(2,–3) и точку пересечения прямых и

6 вариант. Доказать, что четырехугольник A B C D – трапеция, если А(3, 6), В(5, 2), С(–1,–3), D(–5,5).

7 вариант. Записать уравнение прямой, проходящей через точку А(3,1) перпендикулярно к прямой ВС, если В(2,5), С(1,0).

8 вариант. Найти уравнение прямой, проходящей через точку А(–2,1) параллельно прямой MN, если М(–3, –2), N(1,6).

9 вариант. Найти точку, симметричную точке М(2,–1) относительно прямой .

10 вариант. Найти точку О пересечения диагоналей четырехугольника ABCD, если А(–1, –3), В(3,5), С(5,2), D(3, –5).

11 вариант. Через точку пересечения прямых , провести прямую, параллельную оси абсцисс.

12 вариант. Известны уравнения стороны АВ треугольника ABC , его высот ВН АМ . Найти уравнения двух других сторон треугольника ABC.

13 вариант. Даны две вершины треугольника ABC A(–6,2), В(2,–2) и точка пересечения его высот H(1,2). Найти координаты точки М пересечения стороны АС и высоты ВН.

14 вариант. Найти уравнения высот треугольника ABC, проходящих через вершины А и В, если А(–4,2), B(3, –5), С(5,0).

15 вариант. Вычислить координаты точки пересечения перпендикуляров, проведенных через середины сторон треугольника, вершинами которого служат точки А(2,3), В(0,–3), С(6, –3).

16 вариант. Составить уравнение высоты, проведенной через вершину А треугольника ABC, зная уравнения его сторон: (АВ), (АС), (ВС).

17 вариант. Дан треугольник с вершинами А(3,1), В(–3, –1) и С(5,–12). Найти уравнение медианы, проведенной из вершины С, и вычислить ее длину.

18 вариант. Составить уравнение прямой, проходящей через начало координат и точку пересечения прямых и

19 вариант. Найти уравнения перпендикуляров к прямой , проведенных через точки пересечения данной прямой с осями координат.

20 вариант. Даны уравнения сторон четырехугольника: , , , . Найти уравнения его диагоналей.

21 вариант. Составить, уравнения медианы СМ и высоты СК треугольника ABC, если А(4,6), В(–4,0), С(–1,–4).

22 вариант. Через точку Р(5, 2) провести прямую: а) отсекающую равные отрезки на осях координат; б) параллельную оси Ох; в) параллельную оси Оу.

23 вариант. Записать уравнение прямой, проходящей через точку А(–2,3) и составляющей с осью Ох угол: а) 45°; б) 90°; в) 0°.

24 вариант. Какую ординату имеет точка С, лежащая на одной прямой с точками А(–6,–6) и В(–3, –1)и имеющая абсциссу, равную 3?

25 вариант. Через точку пересечения прямых и провести прямую, делящую отрезок между точками А(4 –3) и В(–1,2) в отношении =2/3.

26 вариант. Известны уравнения двух сторон ромба и и уравнение одной из его диагоналей . Найти уравнение второй диагонали.

27 вариант. Найти точку Е пересечения медиан треугольника, вершинами которого являются точки А(–3,1), В(7,5) и С(5, –3).

28 вариант. Записать уравнения прямых, проходящих через точку А(–1,1) под углом 45° к прямой .

29 вариант. Даны уравнения высот треугольника ABC , и координаты его вершины А(2,3). Найти уравнения сторон АВ и АС треугольника.

29 вариант. Даны уравнения двух сторон параллелограмма , и точка пересечения его диагоналей М(3,–1). Найти уравнения двух других сторон.

Решение типового варианта

Задание 7.

Написать общее уравнение и построить прямые, проходящие через т. параллельно:

1. оси Ох;

2. оси Оy;

3. биссектрисе первого координатного угла;

4. биссектрисе второго координатного угла;

5) прямой .

Решение:

1) Т.к. прямая параллельна оси Ох, то в уравнении (3.2) , получаем , или окончательно, .

2) Т.к. прямая параллельна оси Оy, то , т.е. .

3) У биссектрисы 1-го координатного угла угловой коэффициент (т.к. ). Поскольку искомая прямая параллельна биссектрисе 1-го угла, то ее угловой коэффициент также равен 1. по формуле (3.4) получаем:

откуда окончательно имеем .

4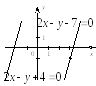) У биссектрисы 2-го координатного угла , получаем , окончательно .

5) Найдем угловой коэффициент прямой , для чего приведем ее общее уравнение к виду (3.3)

По формуле (3.4) получаем уравнение искомой прямой: , откуда .

Задание 8.

Записать общее уравнение и построить прямые, найти их угловые коэффициенты:

1. прямая задана точкой и нормальным вектором ;

2. прямая задана точкой и направляющим вектором ;

3. прямая задана двумя точками и ;

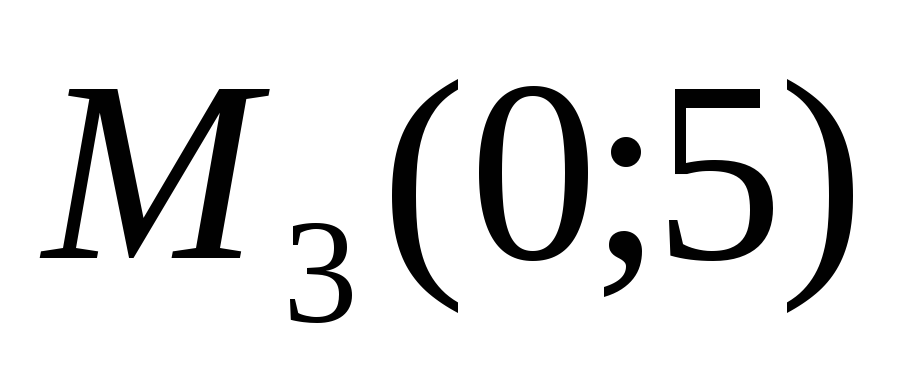4. прямая задана точкой и угловым коэффициентом .

Решение.

1) По формуле (3.2) получаем

;

- общее уравнение прямой.

Для построения прямой ее общее уравнение переводят в уравнение «в отрезках» (3.8):

;

, .

Для определения углового коэффициента данной прямой ее общее уравнение приводят к виду (3.3):

.

2) по формуле (3.5) получаем:

- общее уравнение прямой.

.

3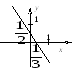) по формуле (3.7) для прямой получаем:

; ;

- общее уравнение прямой.

;

.

4) по формуле (3.4) получаем:

- общее уравнение прямой.

;

.

Задание 9.

Даны вершины треугольника : , , . Построить треугольник и найти:

1. уравнение стороны и ;

2. уравнение высоты ;

3. уравнение медианы ;

4. точку пересечения медианы и высоты ;

5. уравнение прямой, проходящей через вершину параллельно стороне ;

6. угол ;

7. длину высоты .

Решение:

1) Для стороны воспользуемся формулой (3.7)

,

откуда или . Аналогично выводится уравнение стороны :

, откуда .

2) Т.к. для высоты вектор является нормальным то пользуемся уравнением (3.2)

,

откуда .

3) Находим координаты точки М – середины отрезка ВС:

; .

Уравнение медианы составим по формуле (3.7):

; ,

откуда .

4) Для нахождения координат точки пересечения медианы и высоты составляем систему уравнений:

.

Решая ее, получаем .

5) Для искомой прямой вектор является направляющим , поэтому пользуемся формулой (3.5)

,

откуда .

6) Угол найдем как угол между прямыми : и : по формуле (3.9) учитывая, что , :

,

.

7) Длину высоты найдем как расстояние от точки до прямой : по формуле (3.11):

(ед.).

Задание 10. Известны вершины и параллелограмма и точка пересечения его диагоналей . Записать уравнение сторон параллелограмма.

Решение:

Уравнение стороны ОА видно из построении:

ОА: .

Т.к. точка В является серединой диагонали AD, то по формулам деления отрезка пополам получаем координаты вершин D:

; .

Уравнение стороны ОD составим по формуле (3.7):

, откуда получим .

Уравнение стороны АС находим, учитывая, что она параллельна прямой OD с , воспользовавшись формулой (3.2):

, откуда .

Наконец, учитывая параллельность стороны ОА и DC составляем уравнение стороны DC: .