
- •СамарсКий государственНый университет путей сообщения
- •Содержание
- •Аналитическая геометрия
- •I. Прямые и плоскости
- •1. Плоскость
- •Задание 1
- •Задание 2
- •Задание 3
- •2. Прямая в пространстве. Прямая и плоскость
- •Задание 4
- •Задание 5
- •Задание 6
- •3. Прямая на плоскости
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Дополнительные задания
- •1 Вариант
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •5 Вариант
- •6 Вариант
- •7 Вариант
- •8 Вариант
- •9 Вариант
- •10 Вариант
- •11 Вариант
- •12 Вариант
- •13 Вариант
- •14 Вариант
- •15 Вариант
- •16 Вариант
- •17 Вариант
- •18 Вариант
- •19 Вариант
- •20 Вариант
- •21 Вариант
- •22 Вариант
- •23 Вариант
- •24 Вариант
- •25 Вариант
- •26 Вариант
- •II Линии и поверхности второго порядка
- •1. Окружность и сфера
- •2. Эллипс и эллипсоид
- •3. Гипербола и гиперболоиды
- •4. Парабола и параболоиды
- •Задание 11
- •Задание 12
- •Задание 13
- •5. Цилиндры второго порядка. Конус второго порядка
- •6. Поверхности вращения
- •Задание 14
- •Задание 15
- •III. Линии, заданные уравнениями в полярных координатах и параметрическими уравнениями
- •1. Полярные координаты точки и уравнение линии в полярных координатах
- •Задание 16
- •Задание 17
- •Задание 18
- •2. Параметрические уравнения линии
- •Задание 19
Задание 2
Даны
4-е точки
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Составить уравнения:
.
Составить уравнения:
-
плоскости
 ;
; -
плоскости, проходящей через т.
 перпендикулярно вектору
перпендикулярно вектору
 ;
; -
плоскости, проходящей через т.
 и
и
 ,
параллельно вектору
,
параллельно вектору

Вычислить:
-
косинус угла между координатной плоскостью
 и плоскостью
и плоскостью

1
вариант.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2
вариант.
![]() (0,
5, 0),
(0,
5, 0),
![]() (2,
3, –4),
(2,
3, –4),
![]() (0,
0, –6),
(0,
0, –6),
![]() (–3,
1, –1).
(–3,
1, –1).
3
вариант.
![]() (0,
0, 6),
(0,
0, 6),
![]() (4,
0, –4),
(4,
0, –4),
![]() (1,
3, –1),
(1,
3, –1),
![]() (4,
–1, –3).
(4,
–1, –3).
4
вариант.
![]() (2,
–5, 3),
(2,
–5, 3),
![]() (3,
2, –5),
(3,
2, –5),
![]() (5,
–3, –2),
(5,
–3, –2),
![]() (–5,
3, 2).
(–5,
3, 2).
5
вариант.
![]() (6,
0, 4),
(6,
0, 4),
![]() (0,
6, 4),
(0,
6, 4),
![]() (4,
6, 0),
(4,
6, 0),
![]() (0,
–6, 4).
(0,
–6, 4).
6
вариант.
![]() (3,
2, 4),
(3,
2, 4),
![]() (2,
4, 3),
(2,
4, 3),
![]() (4,
3, –2),
(4,
3, –2),
![]() (–2,
–4,–3).
(–2,
–4,–3).
7
вариант.
![]() (6,
3, 5),
(6,
3, 5),
![]() (5,
–4, 3),
(5,
–4, 3),
![]() (3,
5, 6),
(3,
5, 6),
![]() (–6,
–1, 2).
(–6,
–1, 2).
8
вариант.
![]() (5,
–2, –1),
(5,
–2, –1),
![]() (4,
0, 0),
(4,
0, 0),
![]() (2,
5, 1),
(2,
5, 1),
![]() (1,
2, 5).
(1,
2, 5).
9
вариант.
![]() (4,
2, 5),
(4,
2, 5),
![]() (3,
0, 4),
(3,
0, 4),
![]() (0,
0, 3),
(0,
0, 3),
![]() (5,
–2, –4).
(5,
–2, –4).
10
вариант.
![]() (4,
2, –5),
(4,
2, –5),
![]() (3,
0, 4),
(3,
0, 4),
![]() (0,
2, 3),
(0,
2, 3),
![]() (5,
–2, –4).
(5,
–2, –4).
11
вариант.
![]() (4,
4, 10),
(4,
4, 10),
![]() (7,
10, 2),
(7,
10, 2),
![]() (2,
8, 4),
(2,
8, 4),
![]() (9,
6, 9).
(9,
6, 9).
12
вариант.
![]() (4,
6, 5),
(4,
6, 5),
![]() (6,
2, 4),
(6,
2, 4),
![]() (2,
4, 4),
(2,
4, 4),
![]() (1,
5, –3).
(1,
5, –3).
13
вариант.
![]() (3,
5, 4),
(3,
5, 4),
![]() (6,
5, 4),
(6,
5, 4),
![]() (5,
0, 4),
(5,
0, 4),
![]() (4,
–2, 3).
(4,
–2, 3).
14
вариант.
![]() (0,
6, 6),
(0,
6, 6),
![]() (–2,
6, 4),
(–2,
6, 4),
![]() ,(6,
4, 1)
,(6,
4, 1)
![]() (–2,
0, 3).
(–2,
0, 3).
15
вариант.
![]() (1,
4, 2),
(1,
4, 2),
![]() (5,
2, 6),
(5,
2, 6),
![]() (5,
–3, 4),
(5,
–3, 4),
![]() (4,
0, 6).
(4,
0, 6).
16
вариант.
![]() (6,
6, 5),
(6,
6, 5),
![]() (4,
2, 5),
(4,
2, 5),
![]() (4,
6, 1),
(4,
6, 1),
![]() (6,
–4, 3).
(6,
–4, 3).
17
вариант.
![]() (4,
2, 2),
(4,
2, 2),
![]() (5,
1, 1),
(5,
1, 1),
![]() (5,
3, 1),
(5,
3, 1),
![]() (2,
3, 4).
(2,
3, 4).
18
вариант.
![]() (–1,
6, 4),
(–1,
6, 4),
![]() (1,
5, 5),
(1,
5, 5),
![]() (5,
6, 0),
(5,
6, 0),
![]() (3,
3, 6).
(3,
3, 6).
19
вариант.
![]() (2,
1, 3),
(2,
1, 3),
![]() (6,
5, –1),
(6,
5, –1),
![]() (3,
5, 2),
(3,
5, 2),
![]() (0,
4, 1).
(0,
4, 1).
20
вариант.
![]() (–2,
1, 2),
(–2,
1, 2),
![]() (4,
0, 0),
(4,
0, 0),
![]() (3,
2, 6),
(3,
2, 6),
![]() (1,
3, 2).
(1,
3, 2).
21
вариант.
![]() (3,
2, 4),
(3,
2, 4),
![]() (1,
3, 2),
(1,
3, 2),
![]() (–2,
1, 2),
(–2,
1, 2),
![]() (4,
0, 0).
(4,
0, 0).
22
вариант.
![]() (1,
3, 2),
(1,
3, 2),
![]() (3,
2, 0),
(3,
2, 0),
![]() (4,
0, 0),
(4,
0, 0),
![]() (–2,
1, 2).
(–2,
1, 2).
23
вариант.
![]() (3,
1, –2),
(3,
1, –2),
![]() (1,
–2, 1),
(1,
–2, 1),
![]() (2,
2, 5),
(2,
2, 5),
![]() (–2,
1, 0).
(–2,
1, 0).
24
вариант.
![]() (–2,
1, 0),
(–2,
1, 0),
![]() (2,
2, 5),
(2,
2, 5),
![]() (3,
1, 2),
(3,
1, 2),
![]() (1,
–2, 1).
(1,
–2, 1).
25
вариант.
![]() (2,
2, 5),
(2,
2, 5),
![]() (–2,
1, 0),
(–2,
1, 0),
![]() (1,
–2, 1),
(1,
–2, 1),
![]() (3,
1, 2).
(3,
1, 2).
26
вариант.
![]() (1,
–1, 6),
(1,
–1, 6),
![]() (4,
5, –2),
(4,
5, –2),
![]() (–1,
3, 0),
(–1,
3, 0),
![]() (1,
–1, 5).
(1,
–1, 5).
27
вариант.
![]() (6,
1, 5),
(6,
1, 5),
![]() (–1,
3, 0),
(–1,
3, 0),
![]() (4,
5, –2),
(4,
5, –2),
![]() (1,
–1, 6).
(1,
–1, 6).
28
вариант.
![]() (1,
–2, 1),
(1,
–2, 1),
![]() (3,
1, –2),
(3,
1, –2),
![]() (2,
2, 5),
(2,
2, 5),
![]() (–2,
1, 0).
(–2,
1, 0).
29
вариант.
![]() (4,
0, 0),
(4,
0, 0),
![]() (–2,
1, 2),
(–2,
1, 2),
![]() (1,
3, 2),
(1,
3, 2),
![]() (3,
2, 5).
(3,
2, 5).
30
вариант.
![]() (–5,
6, –1),
(–5,
6, –1),
![]() (6,
–5, 2),
(6,
–5, 2),
![]() (6,
5, 1),
(6,
5, 1),
![]() (0,
0, 2).
(0,
0, 2).
Задание 3
Решить следующие задачи.
1
вариант.
Найти величины отрезков, отсекаемых на
осях координат плоскостью, проходящей
через точку
![]() параллельно
плоскости
параллельно
плоскости
![]() .
.
2
вариант.
Составить уравнение плоскости, проходящей
через середину отрезка М1М2
перпендикулярно
к этому отрезку, если
![]() ,
,
![]() .
.
3
вариант.
Найти расстояние от точки
![]() до плоскости
до плоскости
![]() .
.
4
вариант.
Составить уравнение плоскости, проходящей
через точку
![]() параллельно плоскости Оху.
параллельно плоскости Оху.
5
вариант.
Составить уравнение плоскости, проходящей
через ось Ох
и точку
![]() .
.
6
вариант.
Составить уравнение плоскости, проходящей
через точки
![]() ,
,
![]() параллельно
оси Оу.
параллельно
оси Оу.
7
вариант.
Составить уравнение плоскости, проходящей
через точки
![]() и
и
![]() параллельно оси Ох.
параллельно оси Ох.
8
вариант.
Найти величины отрезков, отсекаемых на
осях координат плоскостью, проходящей
через точку
![]() параллельно
плоскости
параллельно
плоскости
![]() .
.
9
вариант.
Составить уравнение плоскости, проходящей
через точки![]() ,
,
![]() параллельно
вектору
параллельно
вектору
![]() .
.
10
вариант.
Составить уравнение плоскости в
"отрезках", если она проходит через
точку
![]() и
отсекает на оси Ох
отрезок
и
отсекает на оси Ох
отрезок
![]() ,
а на оси Oz
– отрезок
,
а на оси Oz
– отрезок
![]() .
.
11
вариант.
Составить уравнение плоскости, проходящей
через точку
![]() параллельно двум векторам
параллельно двум векторам
![]() и
и
![]() .
.
12
вариант.
Составить
уравнение плоскости, проходящей через
точки
![]() ,
,
![]() перпендикулярно к плоскости
перпендикулярно к плоскости
![]() .
.
13
вариант.
Составить
уравнение плоскости, проходящей через
начало координат перпендикулярно к
двум плоскостям
![]() и
и
![]() .
.
14
вариант.
Составить
уравнение плоскости, проходящей через
точки![]() ,
,
![]() параллельно
вектору
параллельно
вектору
![]() .
.
15
вариант.
Составить
уравнение плоскости, проходящей через
начало
координат перпендикулярно к вектору![]() ,
если
,
если
![]() ,
,
![]() .
.
16
вариант.
Найти величины отрезков, отсекаемых на
осях координат плоскостью, проходящей
через точку
![]() параллельно
плоскости
параллельно
плоскости
![]() .
.
17
вариант.
Составить уравнение плоскости, проходящей
через точку
![]() перпендикулярно к отрезку
перпендикулярно к отрезку
![]() ,
если
,
если
![]() ,
,
![]() .
.
18
вариант.
Составить уравнение плоскости, проходящей
через точку
![]() перпендикулярно к отрезку
перпендикулярно к отрезку
![]() ,
если
,
если
![]() ,
,
![]() .
.
19
вариант.
Составить общее уравнение плоскости,
проходящей через точку
![]() параллельно координатной плоскости
Oxz.
параллельно координатной плоскости
Oxz.
20
вариант.
Составить уравнение плоскости, проходящей
через ось Оу
и точку
![]() .
.
21
вариант.
 Составить
уравнение плоскости, проходящей через
точки
Составить
уравнение плоскости, проходящей через
точки
![]() и
и
![]() параллельно
оси Oz.
параллельно
оси Oz.
22
вариант.
Составить уравнение плоскости, проходящей
через точки
![]() и
и
![]() параллельно оси Oу.
параллельно оси Oу.
23
вариант.
Найти проекцию точки
![]() на
плоскость
на
плоскость
![]() .
.
24
вариант.
Определить, при каком значении В
плоскости
![]() и
и
![]() будут перпендикулярны.
будут перпендикулярны.
25
вариант.
Составить уравнение плоскости, которая
проходит через точку
![]() и
отсекает на осях координат отличные от
нуля отрезки одинаковой величины.
и
отсекает на осях координат отличные от
нуля отрезки одинаковой величины.
26
вариант. При
каких значениях А
и В
плоскость
![]() параллельна плоскости
параллельна плоскости
![]() .
.
27
вариант.
Составить уравнение плоскости, проходящей
через точки
![]() ,
,
![]() перпендикулярно к плоскости
перпендикулярно к плоскости
![]() .
.
28
вариант.
Составить
уравнение плоскости, проходящей через
начало координат перпендикулярно к
плоскостям
![]() и
и
![]() .
.
29
вариант.
Составить
уравнение плоскости, проходящей через
точки
![]() и
и
![]() параллельно
вектору
параллельно
вектору
![]() .
.
30
вариант.
Определить, при каком значении С
плоскости
![]() и
и
![]() будут перпендикулярны.
будут перпендикулярны.
Решение типового варианта
Задание 1.
Написать общее уравнение и построить плоскости заданные следующим образом:
-
точкой
 и нормальным вектором
и нормальным вектором
 ;
;
2)
отрезками
![]() ,
,
![]() ,
,
![]() ,
отсекаемыми данной плоскостью на осях
координат
,
отсекаемыми данной плоскостью на осях
координат
![]()
![]() и
и
![]() соответственно;
соответственно;
3)
тремя точками
![]() ,
,
![]() ,
,
![]() ;
;
4)
двумя точками
![]() ,
и
,
и
![]() и направляющим (параллельным) вектором
и направляющим (параллельным) вектором
![]() ;
;
-
найти косинус угла между плоскостями из п.1) и 2);
-
найти расстояние от точки
 до плоскости из п. 3).
до плоскости из п. 3).
Решение:
1) по формуле (1.2) получаем
![]()
![]()
 -
общее уравнение плоскости 1.
-
общее уравнение плоскости 1.
Для построения плоскости рекомендуется перейти к уравнению плоскости «в отрезках» (1.3)
![]()

![]() ;
;
![]() ;
;
![]() - отрезки, отсекаемые плоскостью на осях
координат
- отрезки, отсекаемые плоскостью на осях
координат
![]() ,
,
![]() и
и
![]() соответственно. Соединив концы этих
отрезков получаем часть искомой
плоскости.
соответственно. Соединив концы этих
отрезков получаем часть искомой
плоскости.
2) составляем уравнение плоскости «в отрезках» (1.3) и сразу строим полученную плоскость
![]()

Для получения общего уравнения умножим уравнение «в отрезках» на 6 (н.о.к. знаменателей)
![]()
![]() -
общее уравнение плоскости 2.
-
общее уравнение плоскости 2.
3) составим уравнение плоскости, проходящей через три заданные точки (1.4)
 ;
;

Р азложим
последний определитель по элементам
1-ой строки:
азложим
последний определитель по элементам
1-ой строки:

Итак
![]() - общее уравнение плоскости 3.
- общее уравнение плоскости 3.
Переходим
к уравнению «в отрезках»
 и строим плоскость
и строим плоскость

4)
составим уравнение плоскости через 2-е
точки и направляющий вектор
![]() (1.5):
(1.5):
 .
.
Произведя
действия, аналогичные приведенным в п.
3 получаем
![]() - общее уравнение плоскости 4 и
- общее уравнение плоскости 4 и
уравнение «в отрезках»

Т.к.
в последнем уравнении
![]() ,
получаем частный случай расположения
плоскости – параллельно оси
,
получаем частный случай расположения
плоскости – параллельно оси
![]() .
.
5) Угол между плоскостями 1 и 2:
![]() и
и
![]() находим как угол между их нормальными
векторами
находим как угол между их нормальными
векторами
![]() и
и
![]() по формуле (1.6)
по формуле (1.6)
![]() ;
;
![]() ,
,
![]()
6)
расстояние от точки
![]() до плоскости 3)
до плоскости 3)
![]() найдем по формуле (1.7)
найдем по формуле (1.7)
![]() (ед.)
(ед.)
Задание 2.
Даны
4-е точки
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Составить уравнения:
.
Составить уравнения:
-
плоскости
 ;
; -
плоскости, проходящей через т.
 перпендикулярно вектору
перпендикулярно вектору
 ;
; -
плоскости, проходящей через т.
 и
и
 ,
параллельно вектору
,
параллельно вектору

Вычислить:
-
косинус угла между координатной плоскостью
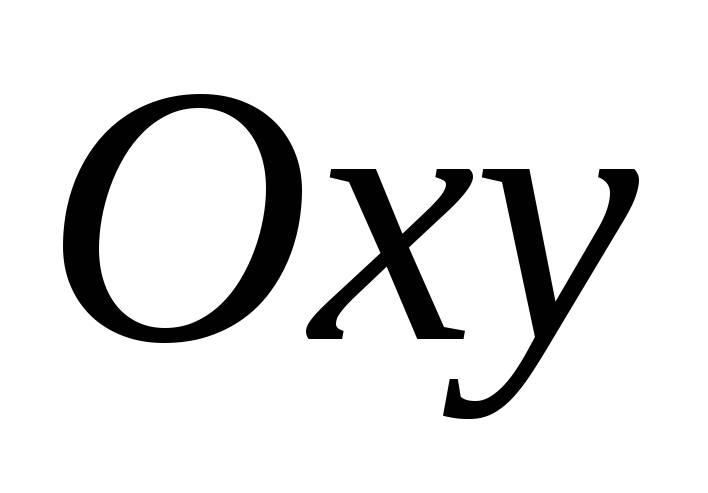 и плоскостью
и плоскостью

Решение:
1)
Уравнение плоскости
![]() составим по формуле (1.4)
составим по формуле (1.4)

![]()
![]() -
общее уравнение плоскости
-
общее уравнение плоскости
![]() .
.
2)
Уравнение плоскости, проходящий через
т.
![]() перпендикулярно вектору
перпендикулярно вектору
![]() составим по формуле (1.2). В данном случае
составим по формуле (1.2). В данном случае
![]()
![]()
![]() -
общее уравнение плоскости.
-
общее уравнение плоскости.
3)
Уравнение плоскости, проходящий через
точки
![]() и
и
![]() ,
параллельно вектору
,
параллельно вектору
![]() составим по формуле (1.5). В данном случае
составим по формуле (1.5). В данном случае
![]()

![]()
![]() -
общее уравнение плоскости.
-
общее уравнение плоскости.
4)
Вычислим косинус угла между координатной
плоскостью
![]() (уравнение имеет вид
(уравнение имеет вид
![]() )
и плоскостью
)
и плоскостью
![]()
![]() по формуле (1.6):
по формуле (1.6):
![]() .
.
Задание
3. Составить
уравнение плоскости, проходящей через
т.
![]() перпендикулярно к двум плоскостям
перпендикулярно к двум плоскостям
![]() и
и
![]() .
.
Решение.
Из уравнений плоскости найдем координаты
их нормалей:
![]() и
и
![]() .
Перемножив их векторно найдем координаты
вектора
.
Перемножив их векторно найдем координаты
вектора
![]() ,
перпендикулярного для нормалей
,
перпендикулярного для нормалей
![]() и
и
![]() ,
т.е. параллельно для двух данных плоскостей
,
т.е. параллельно для двух данных плоскостей

![]() .
.
Вектор
![]() является нормальным для искомой
плоскости. Пользуемся формулой (1.2).
является нормальным для искомой
плоскости. Пользуемся формулой (1.2).
![]()
![]()
![]() -
общее уравнение плоскости.
-
общее уравнение плоскости.
