Классическая теория теплоемкости твердых тел

Рассмотрим диапазон температур, далекий от нуля и температуры плавления. Колеблющийся атом (или ион) в кристаллической решетке обладает 3 степенями свободы. На каждую колебательную степень свободы в среднем приходится энергия, равная kT (сумма двух половинок kT – одна в виде кинетической и одна в виде потенциальной энергии). Следовательно, энергия колебательного движения 1 атома (иона) в кристаллической решетке равна  = 3kT.

Внутренняя энергия одного моля твердого тела равна

U = N_A  = 3kN_AT = 3RT.

Поскольку объем твердых тел при нагревании изменяется мало, их теплоемкость при постоянном давлении незначительно отличается от теплоемкости при постоянном объеме, и говорят просто о молярной теплоемкости твердого тела, которая равна

C_V  C_p = C = dU/dT = 3R  25 Дж/(мольК).

Мы пришли к закону Дюлонга и Пти: атомная (молярная) теплоемкость всех (химически простых кристаллических) твердых тел при достаточно высокой температуре одинакова, равна 3R и не зависит от температуры.

Данный закон выполняется с довольно хорошим приближением для многих химических элементов при комнатной температуре. Однако для бериллия, бора, кремния и алмаза теплоемкость значительно меньше. Это означает, что: 1) на самом деле теплоемкость зависит от температуры; 2) комнатные температуры для бериллия, бора, кремния и алмаза не являются достаточно высокими (например, у алмаза молярная теплоемкость С  3R при температуре t  1800 C).

Если твердое тело является химическим соединением (например, NaCl, MnS), то надо учитывать порознь ионы Na⁺ и Cl ^, колеблющиеся независимо друг от друга, и справедлив закон Джоуля-Коппа: молярная теплоемкость твердого соединения равна сумме атомных теплоемкостей элементов, из которых оно состоит, т.е. равна 3Rn, где n – число атомов в молекуле (для двухатомных кристаллов С = 6R, для трехатомных кристаллов С = 9R).

28. Понятие о квантовой статистике. Распределения

Бозе-Эйнштейна и Ферми-Дирака. Энергия Ферми

Квантовая статистика – раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

При рассмотрении системы многих частиц в классической статистической физике (распределения Максвелла и Больцмана) предполагалось, что частицу можно отличить от всех таких же частиц. Например, если две частицы поменяются местами, то получится новое микросостояние.

Квантовая статистика строится на принципе неразличимости тождественных частиц: все одинаковые частицы (например, все электроны в металлах, все протоны в ядрах атомов) считаются принципиально неразличимыми друг от друга. Если частицы поменяются местами друг с другом, то получится исходное микросостояние.

(Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел: главного, орбитального, магнитного и магнитного спинового. Распределение электронов в атоме подчиняется принципу Паули: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел.)

Все элементарные частицы разделяются на два класса.

К одному классу относятся электроны, протоны, нейтроны и все частицы с полуцелым спином. Эти частицы подчиняются квантовой статистике Ферми-Дирака и поэтому называются фермионами. Фермионы подчиняются принципу Паули, и в данном квантовом состоянии системы фермионов не может находиться более одной частицы. (Аналогия: в одном месте пространства не может находиться больше одного непроницаемого твердого тела.)

К другому классу относятся фотоны, фононы, - и К-мезоны и все частицы с целым спином. Системы таких частиц описываются квантовой статистикой Бозе-Эйнштейна и поэтому называются бозонами. Бозоны не подчиняются принципу Паули: в каждом квантовом состоянии может находиться любое число частиц. (Аналогия: в одном месте пространства возможно одновременное пребывание облаков пара или дыма, лучей света, звуковых волн.)

Основной в квантовой статистике является задача о распределении частиц по координатам и скоростям (энергиям) и нахождении средних значений величин, характеризующих рассматриваемую систему. Для нахождения общего числа всех возможных квантовых состояний системы из N частиц вводится понятие 6N-мерного фазового пространства, так как состояние системы определяется заданием 6N переменных, поскольку состояние каждой частицы определяется тройкой координат x, y, z и тройкой соответствующих проекций импульса p_x, p_y, p_z.

Число частиц, которые могут находиться в одном квантовом состоянии, определяется числами заполнения N_i. Для бозонов числа заполнения могут принимать любые целые значения N_i = 0, 1, 2, 3... Для фермионов возможны только два числа: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения должна быть равна числу частиц в системе. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии N_i. Для этого были получены следующие функции распределения:

– функция распределения Бозе-Эйнштейна, которая определяет среднюю "заселенность" бозонами квантовых состояний с энергией E_i (т.е. среднее число частиц в одном состоянии).

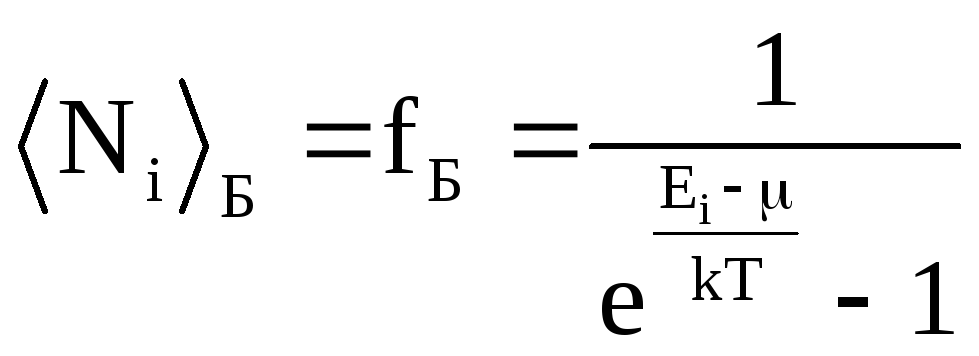
– функция распределения Ферми-Дирака, которая определяет среднее число фермионов N_i_Ф в квантовом состоянии с энергией E_i.

В приведенных формулах: k – постоянная Больцмана; Т – термодинамическая температура. Величина  = (U – TS + pV) / N называется химическим потенциалом, отнесенным к отдельной частице (U – внутренняя энергия системы; S – ее энтропия; V – объем системы; р – давление).

Для бозонов   0, так как иначе получается (из функции распределения), что среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла.

Система частиц (в частности, идеальный газ) называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Параметром вырождения называется величина . При А << 1, т.е. при малой степени вырождения, в квантовых функциях распределений f_Б и f_Ф можно пренебречь единицей в знаменателях и распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана: .

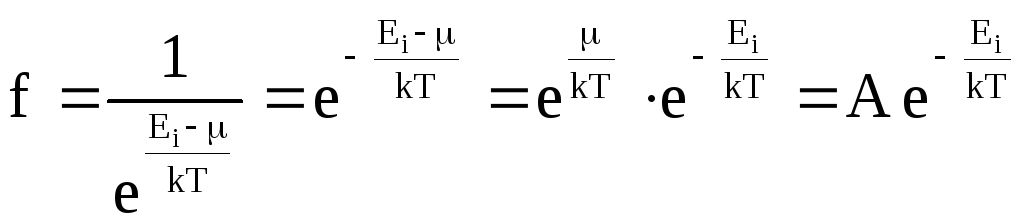Условие малости вырождения имеет вид , где n₀ – концентрация частиц; m – масса частиц; k – постоянная Больцмана; h – постоянная Планка; Т – термодинамическая температура.

Температурой вырождения Т_В называется температура, при которой вырождение становится существенным. Ниже этой температуры отчетливо проявляются квантовые свойства системы частиц. Если Т >> Т_В, то поведение системы частиц (газа) описывается классическими законами. Температура Т_В определяется из условия А = 1:

.

Вырождение газов становится существенным при очень низких температурах и больших плотностях. Например, для водорода при нормальных условиях (Т = 300 К и n₀  3 10²⁵ м^3) параметр вырождения А  3 10^5 << 1. Температура вырождения для водорода Т_В  1 К. Для всех остальных газов, более тяжелых, чем водород, величина А еще меньше. Поэтому газы при нормальных условиях не бывают вырожденными и описываются классической статистикой Максвелла-Больцмана.

Э лектроны проводимости в металлах являются примером вырожденного газа. В обычных условиях n₀  (10²⁸ 10²⁹) м^3. Так как масса электрона мала (m  10^30 кг), то Т_В  2000 К, т.е. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден. Поэтому среднее число электронов N(E), находящихся в квантовом состоянии с энергией Е, описывается функцией распределения Ферми-Дирака:

.

Для электронов (фермионов) среднее число частиц в квантовом состоянии и вероятность заполнения квантового состояния (от 0 до 1) совпадают.

Графики функций Ферми-Дирака для температур Т = 0 и Т > 0 показаны на рис. 83. Такое распределение обусловливается необходимостью соблюдения двух требований: во-первых, полная энергия должна быть минимальной, и, во-вторых, должен соблюдаться принцип Паули. Поэтому при Т = 0 все электроны не могут находиться на самом минимальном энергетическом уровне. Они начинают заполнять квантовые состояния с самого нижнего энергетического уровня, последовательно занимая более высокие квантовые состояния, причем каждое из них лишь одним электроном. Последний электрон занимает уровень с максимальной энергией. Этот уровень называется уровнем Ферми, а энергия уровня – энергией Ферми Е_F. При Т = 0 функция разрывная. При E < E_F функция f_Ф = 1, т.е. все квантовые состояния с такими энергиями заполнены электронами. При E > E_F функция f_Ф = 0, т.е. все квантовые состояния свободны. При этом Е_F = , и распределение Ферми-Дирака обычно записывается в виде

.

Однако такое наглядное определение энергии Ферми имеет смысл лишь в применении к свободным электронам в металле. В общем случае такое определение не точно. Например, в диэлектриках и во многих полупроводниках энергетический уровень Ферми располагается примерно в середине запрещенной зоны, где заведомо нет разрешенных энергетических уровней электронов. Поэтому более общее определение гласит: уровень Ферми – это такой энергетический уровень, вероятность заполнения которого электроном равна 1/2. Это следует из последней формулы при подстановке в нее энергии Е равной E_F.

При температурах Т > 0 функция распределения f_Ф плавно изменяется ("размывается") от 1 до 0 в узкой области (порядка нескольких kT) в окрестности E_F. Причина такого "размытия" в том, что небольшая часть электронов получает дополнительную энергию за счет взаимодействия с тепловыми колебаниями кристаллической решетки. Поскольку средняя энергия теплового движения атомов имеет порядок kT, то и область изменения энергии электронов вблизи уровня Ферми также имеет порядок нескольких kT. В самом деле, подсчитаем значение f_Ф(Е) для энергий Е отличающихся от E_F на 3kT (т.е. E – E_F = 3kT):

; .

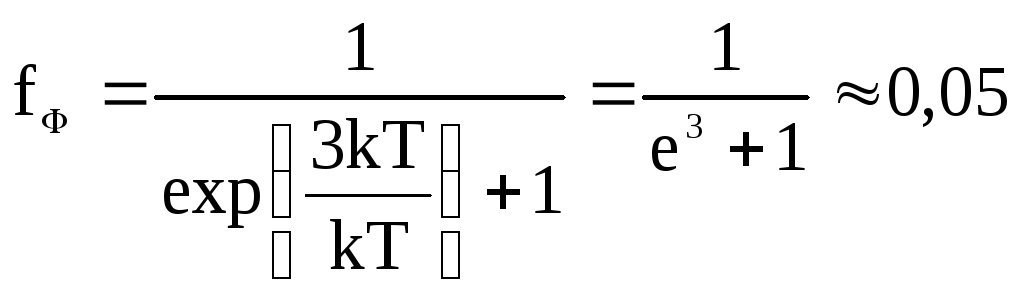В тепловом движении участвует лишь небольшое число электронов, например, при комнатной температуре Т  300 К – это 10^5 от общего числа электронов.