4. Основное уравнение молекулярно-кинетической

теории идеального газа.

Распределение энергии по степеням свободы

Давление газа – макроскопическое проявление теплового движения молекул и результат столкновения молекул со стенками сосуда. При этом молекулы передают стенкам свой импульс. Ввиду хаотичности теплового движения давление газа на все стенки сосуда одинаково.

Давление представляет собой среднюю силу, действующую по нормали на единицу площади поверхности:

или , (11)

где – вектор нормали к поверхности; F_n – проекция вектора силы на нормаль к поверхности. Сила связана с импульсом Р через второй закон Ньютона: . Давление является скалярной величиной. Это подтверждает и закон Паскаля.

Р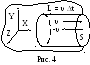ассмотрим упрощенный вывод уравнения. Пусть имеется одноатомный идеальный газ с концентрацией молекул n. Выберем на стенке сосуда малую площадку S и направим оси координат так, как показано на рис. 4. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех осей Х, Y, Z так, что в любой момент времени вдоль каждой оси движется 1/3 часть всех молекул, причем половина из них – в положительном направлении оси, а другая половина – в отрицательном. Поэтому можно считать, что в положительном направлении оси Х движется только 1/6 часть всех молекул.

За время t к площадке S подлетят все молекулы, расположенные в цилиндре с основанием S и высотой L = υ t. Число этих молекул равно .

При упругом ударе о стенку молекула массой m₀ изменяет свой импульс на величину (в проекции на ось Х)

(m₀ υ) = (конеч.) – (нач.) =  m₀ υ  m₀ υ =  2 m₀ υ.

Стенка сосуда получает равный по величине и противоположно направленный импульс, т.е. + 2 m₀ υ.

Найдем суммарный импульс, переданный стенке:

.

Учитывая формулу для давления и второй закон Ньютона, получаем:

.

Так как скорости у молекул разные, то следует пользоваться средним значением квадрата скорости υ². Таким образом, получаем основное уравнение молекулярно-кинетической теории идеального газа:

, (12)

где _ПОСТ – средняя энергия поступательного движения одной молекулы; m₀n =  – плотность газа. Не следует смешивать понятия "средняя квадратичная скорость" и "квадрат средней скорости".

Следствия.

1. Учитывая, что n = N/V, уравнение (12) можно записать в виде

или . (13)

Следовательно, произведение объема газа на его давление численно равно 2/3 кинетической энергии хаотического поступательного движения всех молекул газа, заключенных в этом объеме.

2. Сравним уравнение (13) с уравнением Клапейрона-Менделеева

, получим или

– внутренняя энергия, определяемая для одноатомного идеального газа, как энергия только поступательного движения молекул.

3. Подставим в уравнение (12) известную формулу (5) p = nkT:

, или . (14)

Отсюда следуют два вывода: а) температура – мера средней кинетической энергии движения молекул; б) постоянная Больцмана – коэффициент пропорциональности между температурой и энергией [Дж/К].

4. Из формулы (14) можно найти среднюю квадратичную скорость:

, откуда . (15)

Числом степеней свободы механической системы называется количество независимых величин (координат), с помощью которых можно определить положение системы (в пространстве).

Положение материальной точки (одноатомный газ) полностью определяется тремя координатами (x, y, z) – 3 степени свободы (рис. 5).

Положение абсолютно твердого тела (трехатомный и многоатомный газ) может быть задано тремя координатами центра масс (x, y, z) и тремя углами вращательного движения (, , ) вокруг трех пространственных осей, проходящих через центр масс (рис. 6) – 6 степеней свободы.

Д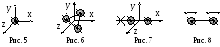 вухатомная молекула (N₂, H₂, O₂) с жесткой связью между атомами имеет 5 степеней свободы (рис. 7): 3 поступательные (x, y, z) и 2 вращательные (, ) вокруг двух осей. Вращение вокруг третьей оси, проходящей через центры двух атомов, не меняет положение молекулы в пространстве.

Формула (12) для давления газа выводилась при условии, что молекулы являются материальными точками, имеющими 3 поступательные степени свободы. Поскольку ни одна из степеней свободы не имеет преимуществ, то энергия, приходящаяся на 1 степень свободы, равна одной третьей части от _ПОСТ. Отсюда следует закон равнораспределения: на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная kT/2 .

При температурах в тысячи градусов связь атомов в молекуле перестает быть жесткой, атомы начинают колебаться (рис. 8). Добавляются колебательные степени свободы, которые имеют двойную энергетическую емкость (энергетический вклад), так как учитываются и кинетическая, и потенциальная энергии атомов.

Итак, средняя энергия одной молекулы равна , (16)

где i – число степеней свободы молекулы, равное сумме поступательных, вращательных и колебательных степеней свободы:

. (17)

Формулу для внутренней энергии идеального газа можно теперь записать в общем виде: . (18)