§3. Активный ненагруженный резерв

Логическая схема сохраняет вид, показанный на рис. , только теперь элементы резерва не могут отказать до момента их включения в работу. Поэтому к параллельному соединению схема не сводится.

Рассмотрим сначала случай только двух элементов, с необязательно одинаковыми функциями надежности R₁(t) и R₂(t) (рис. ).

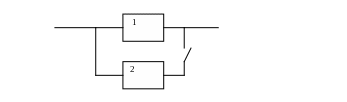
Рис.3.3.1

Вычислим функцию надежности системы, обозначив ее R₁₂(t). Резервированная система будет безотказно работать в течение времени t в двух исключающих друг друга случаях.

1). Основной элемент проработает без отказа в течение времени τ > t; вероятность этого события равна

R₁(t). ( 3.3.1 )

2). Основной элемент откажет на малом интервале [θ, θ+ dθ] с началом в произвольный момент θ из интервала [0, t], а резервный проработает без отказа на оставшемся промежутке (t − θ ).

Вероятность отказа основного элемента при фиксированном значении θ согласно ( ) равна

f₁(θ) dθ,

а с учетом ( )

− R'₁(θ) dθ.

Штрихом обозначена производная.

Вероятность безотказной работы резервного элемента равна

R₂(t − θ).

Вероятность совместного осуществления этих событий равна произведению

− R₂(t − θ)R'₁(θ) dθ. ( 3.3.2 )

Учтем теперь, что момент θ может быть любым внутри интервала [0, t].

По существу это означает, что событие, заключающееся в безотказной работе системы в условиях отказавшего основного элемента, есть сумма описанных несовместных событий, отличающихся моментом отказа. Пользуясь правилом сложения вероятностей и заменяя операцию суммирования интегрированием выражения ( ), получим

− R₂(t − θ)R'₁(θ) dθ. (3.3.3)

Это выражение и есть вероятность события, описанного в начале п.2). Вновь обращаясь к правилу сложения вероятностей и суммируя выражения ( ) и ( ), окончательно получим

R₁₂(t) = R₁(t) − R₂(t − θ)R'₁(θ) dθ. (3.3.4)

Заметим, что вместо приведенного выше подробного вывода этой формулы можно было воспользоваться и известным из теории вероятностей результатом: формулой для функции распределения суммы двух независимых случайных величин – времени безотказной работы основного и времени безотказной работы резервного элемента (формулой композиции двух распределений).

Обратимся теперь к случаю трех элементов. Соответствующую логическую схему можно представить в виде

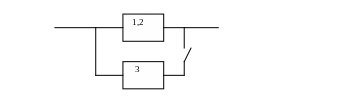
Рис.3.3.2

Здесь символом «1,2» обозначено соединение элементов по схеме рис. . Теперь приведенные выше рассуждения и выкладки можно повторить по отношению к полученной схеме, имея в виду, что функция надежности соединения «1,2» уже известна. Обозначив R₁₂₃(t) функцию надежности системы с тремя элементами и R₃(t) – функцию надежности третьего, получим

R₁₂₃(t) = R₁₂(t) − R₃(t − θ)R'₁₂(θ) dθ. (3.3.5)

По индукции этот результат можно распространить на любое количество k учитываемых элементов в системе

R_12…k(t) = R_12…(k-1)(t) − R_k(t − θ)R'_12…(k-1)(θ) dθ. (3.3.6)

Обозначения здесь введены согласно тем же принципам, что и выше. Эта рекуррентная формула позволяет, начиная с k = 2 и последовательно увеличивая его значения до n – полного числа элементов, определить искомую функцию надежности R_12…n(t) исходной системы.

Трудности вычислений в «буквенном» виде по этой формуле с ростом k быстро возрастают, но возможность получения численных результатов сохраняется. С целью получения некоторых выводов, не зависящих от конкретных числовых данных, рассмотрим частные случаи.

1. Пусть все элементы в системе подчинены одному и тому же экспоненциальному закону надежности с интенсивностью отказов λ. Согласно схеме активного резервирования время безотказной работы системы представляет собой сумму случайных промежутков времени безотказной работы элементов, что соответствует «механизму» образования случайной величины с законом распределения Эрланга (см. гл.2, §3). Согласно формулам ( ) и ( )

R_12…n(t) = e^−λt , (3.3.8)

а соответствующая интенсивность отказов

λ_12…n (t) = 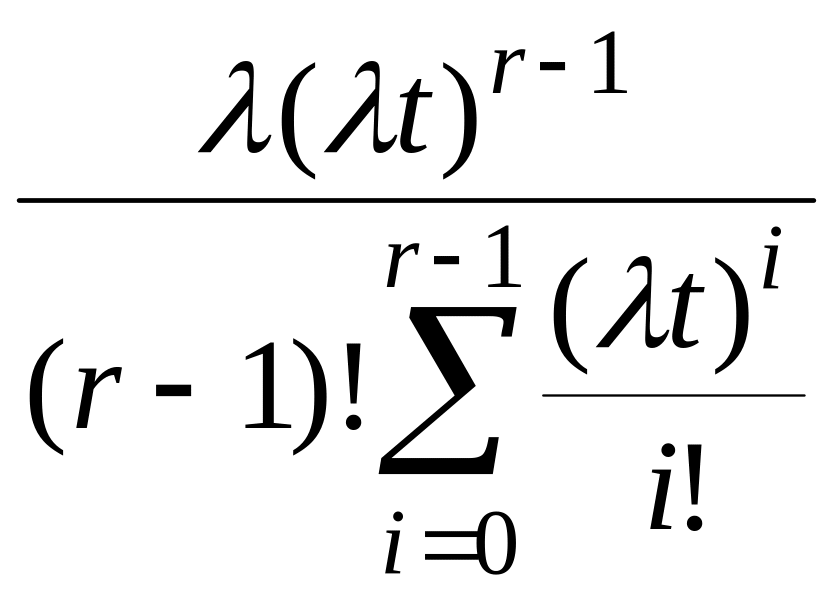. (3.3.9)

В частности для двух элементов

λ₁₂ (t) = . (3.3.10)

График отношения λ₁₂ (t)/λ показан пунктирной кривой на рис. . Эта кривая обнаруживает явное преимущество ненагруженного резерва перед нагруженным. Разумеется, это преимущество сохраняется и при большем количестве резервных элементов, что легко поясняется следующим рассуждением. В системе с нагруженным резервом время ее безотказной работы τ совпадает с максимальным из промежутков времени безотказной работы элементов τ₁, τ₂ , …, τ_n (рис. )

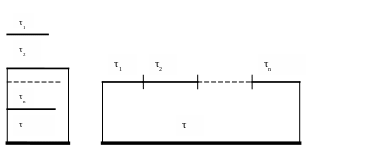Рис.3.3.3

В системе с ненагруженным резервом время ее безотказной работы равно сумме промежутков безотказной работы всех элементов (рис. ). Ясно, что сумма положительных слагаемых всегда больше максимального из них.

Из общих положений теории вероятностей следует также, что математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий. Поэтому в случае активного ненагруженного резерва среднее время безотказной работы резервированной системы T_0рез равно сумме средних времен безотказной работы элементов T_0i (i=1,2 …n) при любых (не обязательно экспоненциальных) законах надежности этих элементов

T_0рез = T_0i . (3.3.11 )

2. Пусть в системе имеется всего один резервный элемент. Функции надежности основного и резервного элементов равны соответственно

R₁ (t)= и R₂ (t)= ,

т.е. подчиняются экспоненциальным законам надежности с разными интенсивностями отказов λ₁ и λ₂. Согласно ( ) получим

R₁₂ (t) = =

= . ( 3.3.12)

Если λ₁ = λ₂ = λ, то после раскрытия получающейся неопределенности типа 0/0 получится тот же результат, что и по формуле ( ) при n = 2

R₁₂ (t) = . (3.3.13 )