Глава 4. Надежность восстанавливаемых систем

§1. Характеристики времени восстановления

При исследовании надежности восстанавливаемых объектов необходимо учитывать свойство ремонтопригодности. Основным показателем ремонтопригодности является функция распределения случайного времени восстановления объекта τ_в – вероятность того, что оно окажется меньше заданного значения t (согласно ГОСТ 27.002-83[ ] – вероятность восстановления в заданное время)

F_в(t) = P(τ_в < t). (4.1.1)

Как известно, наряду с функцией можно использовать и плотность распределения

f_в(t) = . (4.1.2)

В расчетных задачах удобно пользоваться показателем μ(t), аналогичным интенсивности отказов λ(t) и получающимся по формуле, подобной ( )

μ(t) = F′_в(t)/(1 - F_в(t)). (4.1.3)

Его называют интенсивностью восстановления. Подобно λ(t) можно трактовать μ(t) как вероятность восстановления на малом промежутке времени Δt при условии отсутствия восстановления до начала этого промежутка, отнесенную к величине промежутка.

Для расчетных целей важна формула, аналогичная ( )

P(τ_в < t + Δt/ τ_в > t )= μ(t)Δt, (4.1.4)

читаемая так:

«вероятность восстановления на малом промежутке Δt, непосредственно следующем за моментом времени t, при условии, что до этого момента восстановления не произошло, равна μ(t)Δt». По поводу приближенного характера этой формулы можно дать те же комментарии, что и для формулы ( ).

В качестве числовой характеристики времени восстановления используют среднее время восстановления – математическое ожидание τ_в .

T_в = . (4.1.5)

Законы распределения времени восстановления (вид функции F_в(t)) по большей части определяются эмпирически. Могут использоваться и теоретические распределения типов, рассмотренных в §3 гл.2. В частности, получило распространение распределение Эрланга.

Не всегда оправдано, но часто целесообразно для получения обозримых результатов применение экспоненциального распределения (как и в случае с временем безотказной работы). Тогда

F_в(t) =1 – e^-μt , t > 0, (4.1.6)

f_в(t) = μe^-μt , t > 0,

а интенсивность восстановления постоянна (μ = const). При этом аналогично ( )

T_в = 1/ μ, (4.1.7)

Сведения о числовых значениях μ в справочниках не приводятся, поскольку они очень разнятся в зависимости от конкретных условий эксплуатации изделий. При практических расчетах следует руководствоваться опытными данными, производственной статистикой, аналогами.

§2. Простой процесс восстановления

Пусть в момент t = 0 объект начинает работать, а спустя случайный промежуток времени τ₁ происходит отказ, после чего объект восстанавливается за пренебрежимо малое время (мгновенно). Далее следует новый промежуток безотказной работы τ₂, сопровождаемый мгновенным восстановлением и т.д. (рис. ).

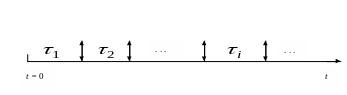
Рис.4.2.1

Если все промежутки времени безотказной работы (i=1,2,…) имеют одинаковую функцию распределения F(t) = P(τ_i < t), то такой процесс называют простым процессом восстановления.

Вообще, простым процессом (или потоком) восстановления называют последовательности любых событий (не обязательно связанных с отказами), разделенных случайными промежутками времени с одинаковым распределением. Название же – из теории надежности, в которой в качестве событий выступают отказы, сопровождаемые мгновенным восстановлением.

Простой процесс восстановления принято характеризовать показателем H(t), представляющим собой математическое ожидание числа отказов-восстановлений за некоторое время t. H(t) и F(t) связаны между собой т.н. уравнением восстановления (без вывода)

. (4.2.1)

Это интегро-дифференциальное уравнение относительно F(t) (если считать

H(t) известным) и интегральное уравнение относительно H(t) (если считать

известной F(t)). Его решение представляет определенные трудности при сложном характере H(t) или F(t). Один из наиболее эффективных методов решения использует преобразование Лапласа.

Применительно к ( ) на основании теоремы свертывания имеем (изображения обозначены теми же буквами, что и оригинал и снабжены символом *; p – переменная преобразования Лапласа L{ })

H*(p) = F*(p) + H*(p) L{ F′(t) }, ( 4.2.2)

и далее на основании теоремы дифференцирования для оригинала

H*(p) = F*(p) + H*(p)[p F*(p) - F(+0)]. ( 4.2.3)

В силу свойств F(t) F(+0) =0, и решения относительно H*(p) или F*(p) имеют вид

H*(p)= , . (4.2.4)

От этих выражений можно перейти к оригиналам и получить решения относительно H(t) или F(t).

В практических приложениях показатель H(t) используется редко. Чаще применяют т.н. параметр потока отказов

, (4.2.5)

представляющий собой среднее число отказов за малую единицу времени непосредственно после момента t. По определению, приведенному в ГОСТ 27.002-83[ ], это «плотность вероятности возникновения отказа восстанавливаемого объекта, определяемая для рассматриваемого момента времени».

Возможно получение оценок показателей H(t) и ω(t) по результатам испытаний. На испытания ставятся N изделий, каждое из которых немедленно заменяется новым в случае отказа. Фиксируется x_i(t) – число отказов (и замен) для каждого изделия c номером i на протяжении времени t, после чего оценка для H(t) находится как среднее арифметическое значений x_i(t)

H̃(t) = 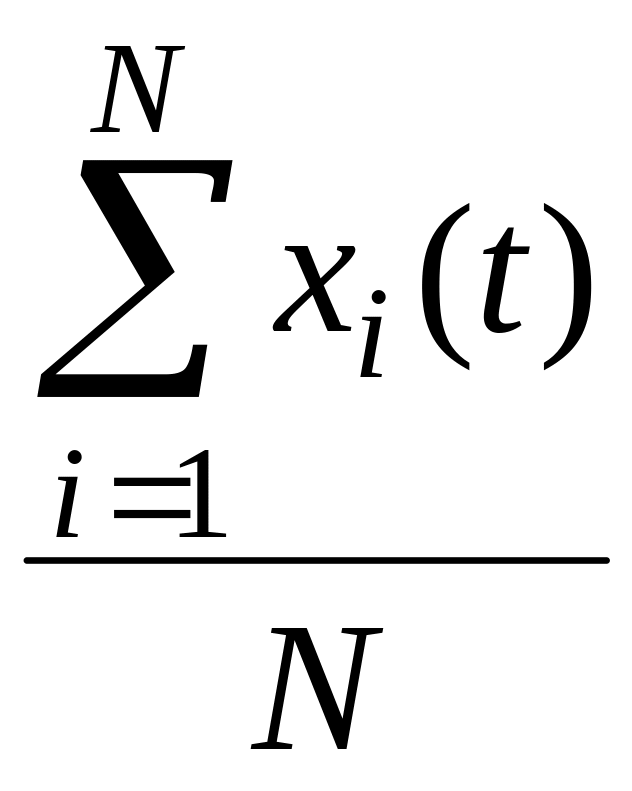. (4.2.6)

При получении оценки ω(t) в формуле ( ) заменяют H(t) на H̃(t), а операцию дифференцирования – вычислением отношения конечных приращений ΔH̃(t)= H̃(t+Δt) - H̃(t) и Δt, где Δt – малый интервал времени, непосредственно следующий за моментом t

ω̃(t) = ΔH̃(t)/ Δt. (4.2.7)

Интервал Δt должен быть не слишком малым, чтобы ω̃(t) не испытывала неприемлемо больших случайных изменений, и в то же время – не слишком большим, чтобы ω̃(t) отражала достаточные подробности в поведении ω(t) . Обычно вопрос выбора Δt становится ясным в ходе испытаний, и сейчас обсуждаться более не будет. Заметим только, что с увеличением N можно брать все меньшие значения Δt.

Существует полезная формула

lim ω(t) = T_о, (4.2.8)

t→∞

где T_о – среднее время безотказной работы.

Рассмотрим распространенный частный случай, когда распределение времени безотказной работы подчинено экспоненциальному закону

F(t) = , t > 0, (4.2.9)

где λ – постоянная интенсивность отказов.

По таблицам преобразования Лапласа имеем

L{1} = 1/p, L{ } = 1/(p + λ), L{t} = 1/p² ,

а значит

F*(p) = ,

что после подстановки в формулу () дает

H*(p)= .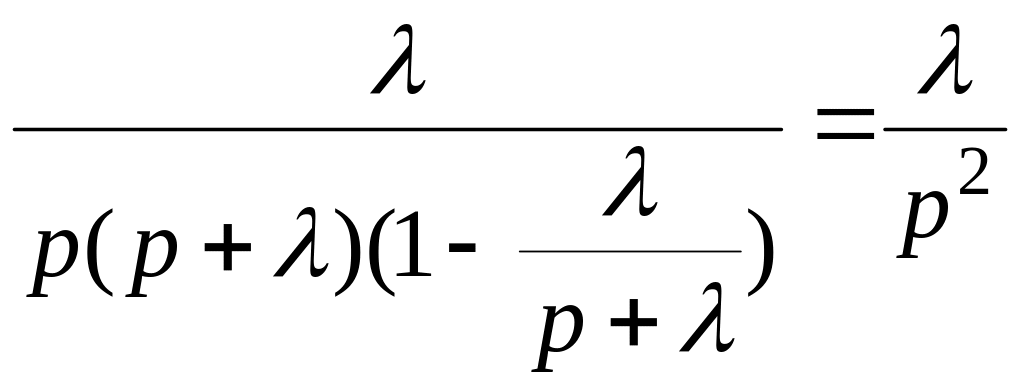

Переходя по таблицам преобразования Лапласа к оригиналу, получим

H(t) = λt, (4.2.10)

а согласно ()

ω(t) = λ. (4.2.11)

Таким образом, параметр потока отказов ω в этом случае от времени не зависит и совпадает с интенсивностью отказов λ. Подчеркнем, что такое совпадение имеет место только для рассматриваемого частного случая.

О небрежности кое-где в литературе.

Имеет место еще один результат (без вывода):

распределение случайного числа X(t) отказов-восстановлений за время t подчиняется закону Пуассона

P(X(t) = n) = , n = 0,1,2,… (4.2.12)

По этой причине процесс рассмотренного типа называют пуассоновским.