§3. Законы распределения наработки до отказа

По-прежнему будем далее подразумевать под наработкой до отказа время безотказной работы.

Существует ряд теоретических законов распределения (говорят также «законы надежности»), которые можно получить, выдвигая определенные гипотезы относительно «механизма» возникновения отказов. Не останавливаясь на этих гипотезах, рассмотрим некоторые наиболее известные из законов. Отметим также, что теоретические законы могут использоваться для приближенного описания законов распределения, полученных по опытным данным.

1). Усеченное нормальное распределение

Плотность обычного (не усеченного) нормального распределения, как известно, дается выражением

f ( t)= . (2.3.1)

Трудность его непосредственного использования состоит в том, что оно описывает случайные величины, которые могут принимать отрицательные значения, тогда как время безотказной работы всегда не меньше 0. Для преодоления этой трудности применяют усеченное нормальное распределение с плотностью f̃(t)

f̃(t) = . (2.3.2)

Здесь с – нормирующий множитель, который обеспечивает сохранение обязательного свойства

f̃(t)dt = 1. (2.3.3)

Из последнего выражения следует

с = 1/( dt). (2.3.4)

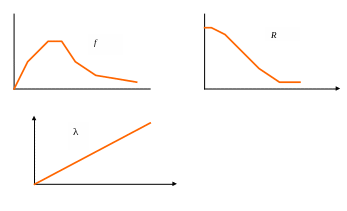
Примерные результаты преобразования f ( t) в f̃(t) приведены на рисунке.

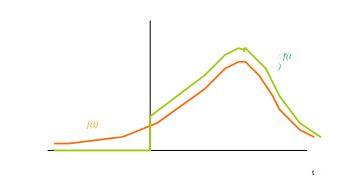
Рис.2.3.1

Согласно ( ) функция надежности принимает вид

R (t) = 1 - f̃(x)dx = f̃(x)dx - f̃(x)dx = f̃(x)dx.

Дальнейшие подстановки дают

R (t) =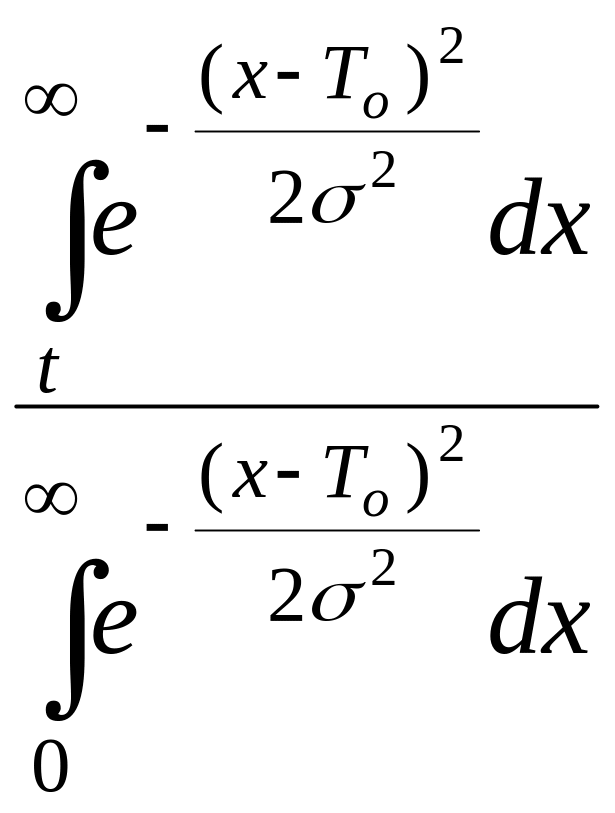 , (2.3.5)

А после замены переменной интегрирования на y=

R (t) =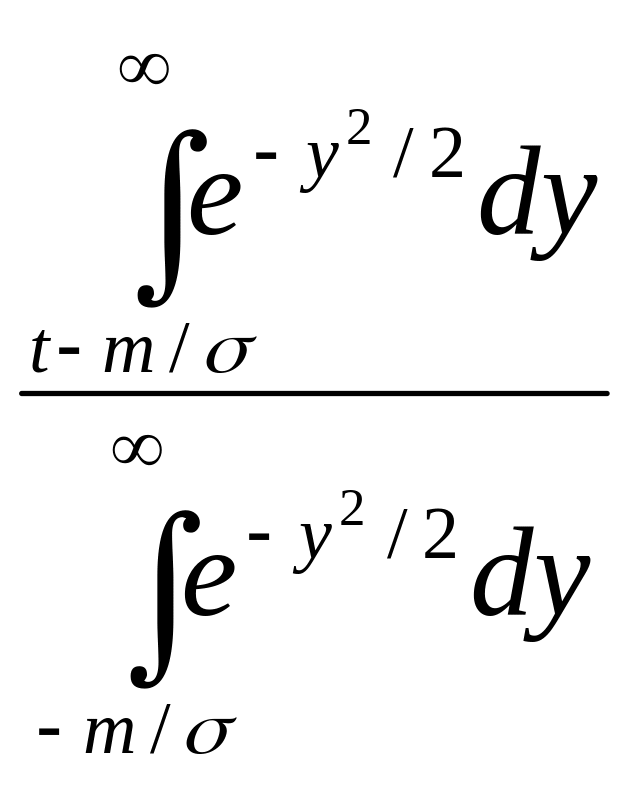 . (2.3.6)

В состав этой формулы входит интеграл, выражающийся через специальную функцию – интеграл вероятности (функция Лапласа) Φ(u)

Φ(u) = , (2.3.7)

таблицы которой имеются в литературе. Φ(u) обладает свойствами

Φ(0)=0; Φ(−u)= −Φ(u); Φ(∞)=1/2; Φ(−∞)= −1/2. (2.2.8)

Выражение R (t) через функцию Лапласа имеет вид

R (t) = , t > 0. (2.3.9)

Примерный вид λ-характеристики в случае усеченного нормального распределения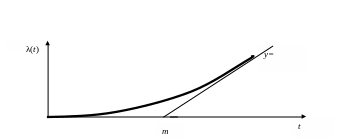

Рис.2.3.2

Как правило, среднее время безотказной работы T_о значительно превосходит стандартное отклонение σ, и отношение T_о /σ не бывает меньше 3. При этом множитель с почти равен 1 (превосходя ее не более, чем на 0,001), и на практике обычно оказывается возможным пользоваться не усеченным нормальным распределением, игнорируя вероятность появления отрицательных значений времени безотказной работы.

2). Распределение Рэлея

Для этого распределения

f ( t)= exp(−t²/ 2s² ),

R (t) =exp(−t² / 2s² ),

λ(t) = t/s², (2.3.10)

T_о = s .

σ = 0,4292s.

Оно содержит единственный параметр s (мода).

3).Распределение Эрланга

Это частный случай т.н. Г-распределения при его целочисленном параметре.

f ( t)=λ₀

R (t)=exp(-λ₀t) , (2.3.11)

λ(t) = ,

T₀ =n/λ₀ .

При этом λ₀=const, а r может принимать целочисленные значения 1,2,3…. (при дробных r получается общий случай Г-распределения, формулы для которого здесь не приводятся).

Распределение Эрланга соответствует одному из упомянутых «механизмов»: время безотказной работы складывается из r случайных промежутков, каждый из которых характеризуется постоянной интенсивностью отказов λ₀ (постоянной интенсивности отказов соответствует распределение, которое подробно рассмотрено ниже).

4). Распределение Вейбулла

R (t)= exp(−bt^a),

λ(t) = abt^a-1 , (2.3.12)

T₀ = b^-1/a Г(1/a + 1).

Распределение Вейбулла имеет два параметра a и b. Оно удобно тем, что при изменении a кривые λ(t) существенно меняют характер своего поведения, что позволяет, например, использовать это распределение для аппроксимации экспериментальных зависимостей.

t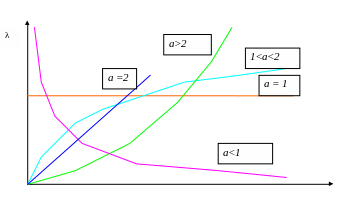

О других распределениях.