§7. Расчет надежности систем с последовательным (основным)

соединением элементов

Вероятности безотказной работы системы R(t) и элементов R₁(t), R₂(t), …, R_n(t) представляют собой вероятности событий, ранее обозначенных S, S₁, S₂, …, S_n. Примем дополнительно предположение, что события, заключающиеся в безотказной работе отдельных элементов, независимы. Это означает, что вероятность безотказной работы каждого элемента не зависит от того, в каком состоянии – работоспособном или нет – находятся другие элементы системы. Тогда по теореме (иногда говорят «по правилу») умножения вероятностей для независимых событий имеем

R(t) =R₁(t)∙ R₂(t)∙ …∙ R_n(t),

т.е. вероятность безотказной работы системы равна произведению вероятностей безотказной работы всех входящих в нее элементов. Это одна из основных расчетных формул, имеющих непосредственное практическое значение.

Определив R(t) и пользуясь формулами связи между R(t), F(t) и f(t) , можно найти и две последних характеристики. Однако в число нормируемых показателей надежности они не входят. С этой точки зрения представляет интерес среднее время безотказной работы T_о ( можно найти по формуле ( )) и в особенности – интенсивность отказов системы λ(t).

Введем λ₁(t), λ₂(t), …, λ_n(t) – интенсивности отказов элементов (согласно исходной постановке задачи – известные). Пользуясь формулами ( ) и ( ), получим

= ∙ ∙…∙

или

= .

Логарифмируя это равенство и дифференцируя полученные выражения по t, найдем

λ(t) = . (2.7.1)

Таким образом, интенсивность отказов системы равна сумме интенсивностей отказов элементов. Эта элементарная и важная в практическом отношении формула служит еще одним объяснением распространению λ-характеристик в расчетах надежности.

Действия по формуле ( ) легко выполняются численно или графически, если λ-характеристики заданы в виде экспериментальных кривых. Вычисления особенно упрощаются, если для элементов справедлив экспоненциальный закон надежности, когда их интенсивности отказов постоянны. Тогда в формуле ( ) аргумент t можно опустить, а действия по ней сводятся к однократному суммированию. При этом интенсивность отказов системы также оказывается постоянной, что приводит к важному выводу: в случае основного соединения экспоненциальный закон надежности для элементов сохраняется и для системы в целом.

Заметим в заключение, что принятое ранее предположение о независимости событий, заключающиеся в безотказной работе отдельных элементов, не слишком ограничивает возможности применения полученных выше результатов. Практически оно означает, что при определении показателей надежности элементов должны учитываться условия их совместной работы в системе.

§8. Расчет надежности систем с параллельным соединением элементов

и соединением общего вида

Переходя к параллельному соединению, рассмотрим сначала формулу ( ). Если бы события S₁, S₂, …, S_n были несовместны, то вероятность безотказной работы системы (события S) можно было вычислить по формуле (правилу) сложения вероятностей путем простого суммирования R₁(t), R₂(t), …, R_n(t). Однако эти события несовместными считать нельзя, поскольку безотказная работа какого-либо элемента отнюдь не исключает безотказной работы любого из остальных. Поэтому при вычислении суммы событий пришлось бы пользоваться обобщенной формулой, которая при двух элементах имеет вид

R(t) =P(S₁+S₂ )=R₁(t)+ R₂(t) − R₁(t)R₂(t),

при трех

R(t) = R₁(t)+ R₂(t) + R₃(t) − R₁(t)R₂(t)− R₁(t)R₃(t)− R₂(t)R₃(t)+

+R₁(t)R₂(t)R₃(t).

При большом количестве элементов формулы этого типа приобретают громоздкий вид, и гораздо удобнее исходить из формулы связи между вероятностями противоположных событий и из формулы ( ). В результате получим

R(t) = 1− P(S̃) = 1 − (1−R₁(t))∙(1 − R₂(t))∙ …∙(1 − R_n(t)). (2.8.1)

Формула для интенсивности отказов системы с параллельным соединением не сулит никаких упрощений по сравнению с общим выражением ( ), из-за чего и приводить ее нецелесообразно. Отметим также, что замечательное свойство последовательного соединения, согласно которому экспоненциальный закон надежности для элементов сохраняется и для системы, не имеет места при параллельном соединении и при любых соединениях общего вида, примеры расчета которых рассматриваются ниже.

При расчете вероятности безотказной работы параллельно-последовательного соединения удобно совместно использовать формулы ( ) и ( ). Так для схемы рис. имеем

R = 1 − (1−R₁₂)(1 −R₃₄₅) =

= 1 − (1−R₁R₂)(1 −R₃R₄₅) =

= 1 − (1−R₁R₂)(1 −R₃(1−(1−R₄)(1−R₅))).

Индексы при R расставлены здесь так же, как для событий в §6, а аргумент t для краткости записи опущен.

Вероятность безотказной работы схем, не сводящихся к параллельно-последовательному соединению, можно рассчитать на основе формулы полной вероятности. Покажем это на примере схемы рис . Выделим элемент 5 и свяжем с ним два противоположных события S₅ и S̃₅ . По формуле полной вероятности имеем

P(S) = P(S/S₅)P(S₅) +P(S/S̃₅)P(S̃₅),

Первые сомножители в правой части это условные вероятности события S при наличии событий S₅ (элемент 5 не отказал) и S̃₅ (элемент 5 отказал). Этим событиям соответствуют схемы,

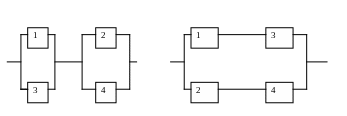
каждая из которых уже представляет собой параллельно-последовательное соединение.

Переходя к символам вероятностей безотказной работы и используя изложенные выше схемы вычислений, получим

R= (R₁+R₃−R₁R₃)(R₂+R₄−R₂R₄)R₅ + (R₁R₃ +R₂R₄ − R₁R₃R₂R₄)(1−R₅).