§4. Расчет надежности (расчет надежности составляет основное содержание лекций; в упоминаемом параграфе приводятся только общие положения о расчете)

§5. Испытания на надежность

§6. Система стандартов по надежности

ГЛАВА 2. НАДЕЖНОСТЬ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ

§1. Функция распределения времени безотказной работы и связанные с ней характеристики

Для невосстанавливаемых объектов (систем) свойства ремонтопригодности и долговечности не имеют смысла. Свойство сохраняемости впредь рассматриваться не будет. Поэтому представляет интерес только свойство безотказности. Вообще говоря, следовало бы в связи с изучением этого свойства пользоваться общим термином «наработка до отказа». Однако, учитывая направленность курса на анализ надежности автоматизированных систем, целесообразно под наработкой подразумевать время работы системы, под наработкой до отказа – время работы от начала эксплуатации до первого (и единственного) отказа или, как будем говорить далее, время безотказной работы. Отметим, что все последующие выводы остаются справедливыми и в случае иного смысла, вкладываемого в понятие «наработка».

Пусть в момент t=0 объект начинает работать, а в момент t=τ происходит отказ. Промежуток τ и составляет время безотказной работы. Как уже подчеркивалось, отказ является случайным событием, а значит τ – случайная величина, для описания которой может быть использованы средства, предоставляемые теорией вероятностей.

Во-первых, это функция распределения времени безотказной работы как случайной величины, т.е. вероятность того, что этот время окажется меньше наперед заданного значения t; обозначим эту функцию F(t)

F( t)= P(τ < t). (2.1.1)

Далее везде символ P(…) будет означать вероятность события “…”, заключенного в скобки.

Поскольку отсчет времени ведется от 0, то F(t)=0 при t<0, а с увеличением времени стремится к 1 (рис. 2.1.1).

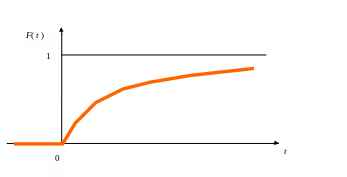
Рис.2.1.1

Наряду с F(t) можно рассматривать и плотность распределения f(t), как известно, связанную F(t) формулами

f(t)= , F(t) = . (2.1.2)

Плотность распределения, умноженная на некоторый малый промежуток времени dt имеет смысл вероятности отказа на малом промежутке dt, непосредственно следующем за моментом времени t.

f(t) dt = P(t < τ< t+ dt). (2.1.3)

Этот результат, как и приведенные выше формулы, вытекает из общих положений теории вероятностей.

В теории надежности вместо функции распределения принято рассматривать вероятность безотказной работы R(t), т.е. вероятность того, что время безотказной работы окажется больше заданного времени t

R(t)= P(τ > t). (2.1.4)

В отличие от F(t) с увеличением надежности R(t) также увеличивается, а с течением времени – убывает.

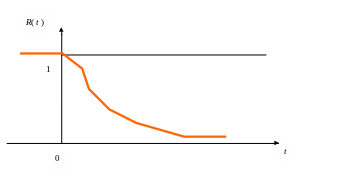
Рис.2.1.2

В литературе встречается термин «функция надежности» .Будем его использовать тоже.

Имеют место очевидные формулы

R(t)=1 − F(t). (2.1.5)

f(t)= − . (2.1.6)

В теории надежности широко используется еще один показатель (не типичный для теории вероятностей) – интенсивность отказов λ(t). Прежде чем дать его определение, поставим следующий вопрос. Пусть известно, что объект проработал без отказа в течение некоторого времени t; какова вероятность, что он откажет на промежутке Δt , непосредственно следующем за t ? Иными словами, ищется условная вероятность события «τ < t+ Δt» при условии, что имеет место событие «τ > t». Пользуясь принятыми в теории вероятностей обозначениями и формулами для условных вероятностей, найдем

P(τ < t+ Δt/ τ >t )= P(τ < t+ Δt, τ > t )/ P( τ > t ). (2.1.7)

В числителе правой части стоит вероятность совместного осуществления событий «τ < t+ Δt» и «τ > t», в знаменателе – вероятность условия. Пользуясь понятием противоположного события, далее получим

P(τ < t+ Δt/ τ > t )=1 − P(τ > t+ Δt, τ > t )/ P( τ > t ),

а затем

P(τ < t+ Δt/ τ > t )=1− P(τ > t+ Δt )/ P( τ > t ),

поскольку для совместного осуществления событий «τ > t+ Δt» и «τ > t» достаточно реализации первого из них. Дальнейшие преобразования с использованием определения вероятности безотказной работы дают

P(τ < t+ Δt/ τ > t )=[ P( τ> t ) − P(τ > t+ Δt )]/ P( τ > t)=

= - Δt {[R (t + Δt) − R (t )]/ Δt}/ R (t ).

Отношение в фигурных скобках при достаточно малых Δt может рассматриваться как производная функции R(t); обозначив ее штрихом, получим

P(τ < t + Δt/ τ > t )= Δt [ − R' (t)/ R (t )]. (2.1.8)

Таким образом, искомая условная вероятность отказа пропорциональна промежутку Δt , что вполне естественно для любого объекта независимо от его надежности, и некоторому выражению, стоящему в квадратных скобках, которое, напротив, характеризуется вероятностью безотказной работы объекта. Это выражение и служит определением интенсивности отказов

λ(t) = − R' (t)/ R (t). (2.1.9)

Учитывая ( ), можно записать последнюю формулу и в виде

λ(t) = F' (t)/(1- F (t)). (2.1.10)

Сравнивая формулы ( ) и( ), можно трактовать λ(t) как вероятность отказа на малом промежутке времени Δt при условии безотказной работы до начала этого промежутка, отнесенную к величине промежутка.

Формулу ( ) можно представить в виде

P(τ < t + Δt/ τ > t )= λ(t)Δt (2.1.11)

и прочитать так:

«вероятность отказа на малом промежутке Δt, непосредственно следующем за моментом времени t, при условии, что до этого момента отказа не произошло, равна λ(t)Δt».

Вообще говоря, равенство ( ) – приближенное, переходящее в точное при Δt→0 (говорят еще: «равенство записано с точностью до величин второго и выше порядка точности относительно Δt»). Однако при правильном выборе Δt им можно пользоваться в практических расчетах, а особенно эффективно его использование в аналитических выкладках, сопровождаемых предельным переходом при Δt→0.

Понятно, что анализ надежности объекта не с самого начала эксплуатации, а по истечении определенного времени его безотказной работы, который приводит к понятию интенсивности отказов, представляет определенный практический интерес. Это частично объясняет причину использования в теории надежности этого показателя. Есть и другие причины, о которых будет сказано позже.

Все рассмотренные характеристики надежности однозначно связаны между собой, и любая из них может быть определена, если известна одна из остальных. Это ясно из приведенных выше формул, которые остается дополнить формулой, позволяющей найти одну из функций F(t), f(t) или R (t) по известной λ(t). Равенство ( ) можно рассматривать как дифференциальное уравнение

R' (t) + λ(t) R (t) = 0 (2.1.12)

относительно R (t), дополнив его условием, вытекающим из свойств R (t)

R (0) = 1. (2.1.13)

Решение этого линейного уравнения с переменным коэффициентом λ(t) хорошо известно из общей теории дифференциальных уравнений и имеет вид

R (t) = exp(− ) (2.1.14)

(x – переменная интегрирования, для которой можно использовать любое обозначение).

Последнее равенство и замыкает группу формул, связывающих рассмотренные характеристики. Любая из них исчерпывающим образом описывает продолжительность безотказной работы τ как случайную величину и является в общем случае функцией времени.

Во многих случаях для упрощения действий или из-за недостатка данных используют числовые характеристики времени безотказной работы, не являющиеся исчерпывающими, но облегчающие расчет надежности. Наиболее употребительной из них является средняя наработка до отказа T_о – математическое ожидание наработки до первого отказа или, согласно принятой договоренности, среднее время безотказной работы. По общей формуле для математического ожидания имеем

T_о = . (2.1.15)

Применив формулу интегрирования по частям и формулу связи между f(t) и R (t), можно выразить T_о через R (t)

T_о = − t R (t) | + . (2.1.16)

Первое слагаемое здесь обращается в 0 при t=0. Пределом этого слагаемого при t также является 0, так как реальные R (t) убывают на бесконечности быстрее, чем 1/ t. Окончательно имеем

T_о = . (2.1.17)

Еще одна употребительная характеристика – дисперсия времени безотказной работы D

D= . (2.1.18)

Можно выразить D и через R (t)

D= 2 - T_о². (2.1.19)

Вместо дисперсии часто используют среднеквадратическое (стандартное) отклонение σ

σ = . (2.1.20)

Характеристики R (t), λ(t) и T_о относятся к числу единичных показателей надежности (см. гл.1, §2).

Анализ размерностей обнаруживает, что R(t) – безразмерный показатель, λ(t) имеет размерность, обратную времени, и T_о – размерность времени. В теории надежности принято исчислять время во внесистемных единицах – часах. Поэтому единицей измерения T_о обычно является также час, а λ(t) – 1/час.