§5. Расчет надежности восстанавливаемой системы (режим 1)

Задачей расчета будем считать вычисление коэффициента готовности системы по известным показателям безотказности и ремонтопригодности входящих в нее элементов. Предположим, что отказ каждого элемента приводит к отказу системы (основное соединение элементов) и что отказы независимы (отказ какого-либо элемента не влияет на показатели надежности других).

Дополнительно предположим, что при отказе одного элемента и до конца его восстановления работа системы приостанавливается, сохранившие работоспособность элементы прекращают функционировать и вплоть до восстановления отказавшего элемента сами отказать не могут. Это предположение и соответствует режиму 1. Оно означает также, что в любой момент времени в системе может быть не более одного отказавшего элемента.

Пусть в системе n элементов, и элемент с номером i характеризуется экспоненциальным распределением времени безотказной работы и восстановления с интенсивностями λ_i и μ_i соответственно (i = 1,2,…,n). Наряду с этими показателями можно ввести среднее время безотказной работы T_oi и T_вi для каждого элемента

T_oi =1/ λ_i , T_вi = 1/ μ_i . (4.5.1)

Рассмотрим (n + 1) состояний системы и перенумеруем их числами 0, 1, 2,…, n, означающими, что в системе нет отказов, отказал и восстанавливается элемент 1, 2, ... , элемент n. Введем вероятности P_i(t) того, что в системе реализуется состояние с номером i в момент времени t.

Рассмотрим далее момент (t+Δt) и запишем уравнения связи между вероятностями, относящимися к моментам t и t+Δt. Для вероятности P₀(t+Δt) получим на основании теорем сложения и умножения вероятностей

. (4.5.2)

Первое слагаемое правой части это вероятность того, что в момент t имело место состояние «0» и за Δt оно сохранилось ( не произошло отказов ни одного элемента). Второе слагаемое – вероятность того, что в момент t какой-то из элементов был неработоспособен, и за Δt произошло его восстановление. Третье слагаемое объединяет вероятности всех остальных событий, возможных при переходе от t к (t+Δt). Оно имеет порядок малости (Δt)² и выше по причинам, уже обсуждавшимся в предыдущем параграфе.

Приведя ( ) к виду

(4.5.3)

и перейдя к пределу при Δt→0, получим

. (4.5.4)

Для вероятности состояния с любым другим номером i=1,2,…,n подобным же образом найдем

и далее

, i=1, 2, … , n. (4.5.5)

Уравнения ( ) и ( ) образуют систему (n+1) дифференциальных уравнений с (n+1) неизвестными вероятностями. Ограничимся отысканием ее установившегося, не зависящего от времени решения, для чего приравняем все производные 0, а в обозначениях вероятностей опустим аргумент t. Получим систему теперь уже алгебраических уравнений

(4.5.6)

, i=1, 2, … , n. (4.5.7)

Это система однородных уравнений, поэтому ее решение либо не существует, либо оно не единственно. Можно убедиться, что имеет место второй случай. Пользуясь ( ), выразим вероятности P_i (i=1, 2, … , n) через P₀

. (4.5.8)

Из оставшегося уравнения ( ) P₀ не определится, поскольку это уравнение удовлетворяется тождественно. Однако можно привлечь еще одно уравнение

P₀ + P₁ + … P_n = 1, (4.5.9)

вытекающее из того факта, что события, которым соответствуют входящие в сумму вероятности, несовместны и образуют полную группу (уравнение ( ) часто называют условием полноты).

Теперь можно найти P₀

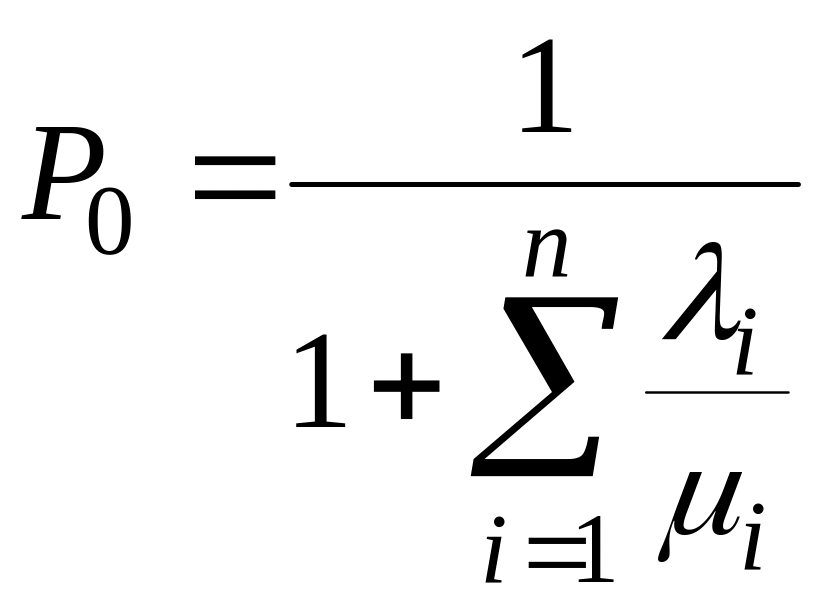, (4.5.10)

а вслед за тем и все остальные вероятности. Впрочем, в их нахождении необходимости нет, поскольку вероятность P₀ по существу и есть коэффициент готовности. Поэтому с учетом ( ) вместо ( ) получаем окончательную расчетную формулу

K_г = 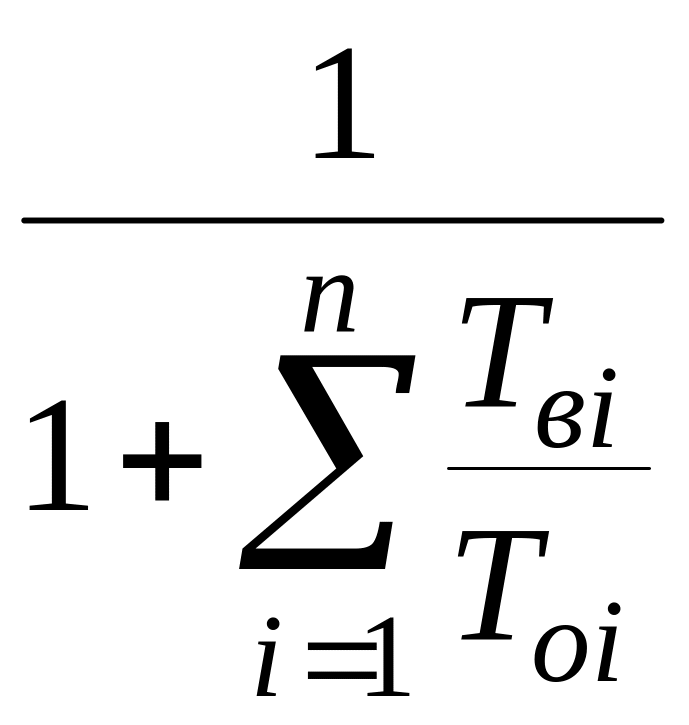. (4.5.11)

Введем коэффициенты готовности отдельных элементов по формулам

K_гi = , i = 1, 2, … , n, (4.5.12)

Эти коэффициенты характеризовали бы надежность каждого элемента при условии, что его отказы возникают и устраняются независимо от состояний, в которых находятся другие элементы системы. Тогда можно привести ( ) к виду

K_Г = 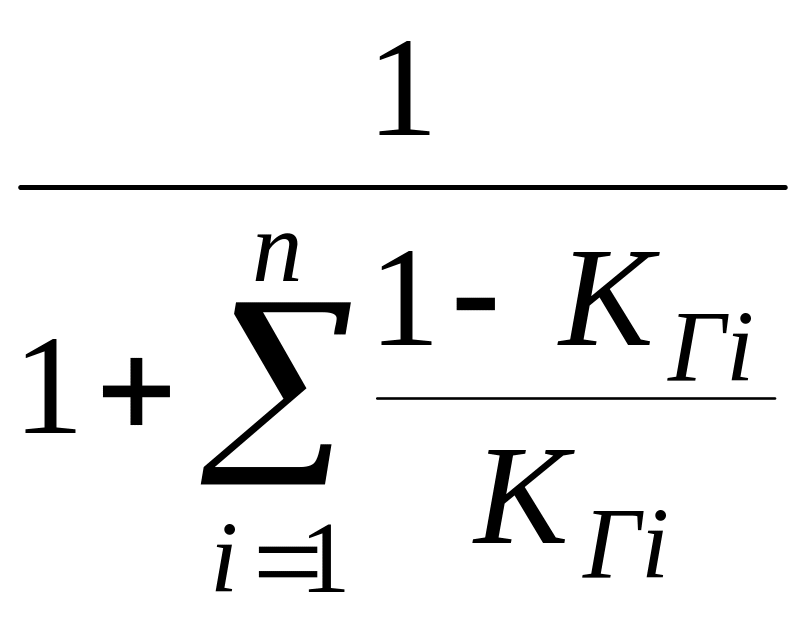. (4.5.13)