
- •Оглавление Введение. Экономика и математика Часть I. Линейные модели и методы в экономике.
- •Глава 1. Принятие решений в экономике
- •Глава 2. Линейное программирование. Теоретические основы и алгоритмы.
- •Глава 3. Теория двойственности в линейном программировании и ее экономические приложения.
- •Глава 4. Транспортная задача и ее приложения.
- •Глава 5. Задача целочисленного линейного программирования
- •Введение. Экономика и математика
- •Часть I. Линейные модели и методы в экономике.
- •Глава 1. Принятие решений в экономике.
- •1.1. Моделирование
- •1.2. Математическое моделирование.
- •1.3. Алгоритм исследования операции.
- •Алгоритм исследования операций.
- •1.4. Примеры исследования операции (моделирование)
- •1.5.Классификация моделей и методов исследования операций
- •Глава 2.
- •2.1. Постановки задачи линейного программирования
- •Основная задача линейного программирования (ОснЗлп)
- •Каноническая задача линейного программирования (кзлп)
- •2.2. Выпуклые множества.
- •0Пределение 2.4.
- •2.3. Теоретические основы линейного программирования
- •2.4. Графический метод и анализ решения злп
- •Проведем графический анализ решения (модели) на чувствительность.
- •2.5. Симплекс-метод решения злп.
- •Определение к-матрицы кзлп
- •Переход от одной к-матрицы злп к другой к-матрице
- •Симплекс-разность к-матрицы злп
- •Алгоритм симплекс-метода
- •2.6. Двойственный сиплекс-метод (р-метод)
- •Определение р-матрицы злп
- •Условия перехода от одной р-матрицы злп к другой
- •Решение задач р-методом
- •2.7.Метод искусственного базиса Назначение и принцип работы методов искусственного базиса
- •2.8. Модифицированный симплекс-метод Постановка задачи
- •Алгоритм модифицированного симплекс-метода
- •Решение задачи модифицированным симплекс-методом
- •2.9. Решение злп на основе Ms Excel
- •Глава 3. Теория двойственности в линейном программировании и ее экономические приложения.
- •3.1. Определение двойственной задачи:
- •3.2. Основные теоремы двойственности
- •3. 3. Экономическая интерпретация двойственности
- •Экономическое содержание теории двойственности.
- •3.4.Применение теории двойственности к решению задач. Применение теоремы 3.5 к решению дз.
- •3.5. Анализ решения злп на основе отчетов ms excel
- •2. Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов.
- •3. Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального плана, то есть номенклатура выпускаемой продукции, остается без изменения.
- •4. Определите суммарную стоимостную оценку ресурсов (себестоимость), используемых при производстве единицы каждого изделия. Производство какой продукции нерентабельно?
- •5. На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции?
- •6. На сколько можно снизить запас каждого из ресурсов, чтобы это не привело к уменьшению прибыли?
- •8. Определите оптимальное решение задачи для случая, когда вектор ресурсов задан в виде .
- •9. Определите интервалы изменения цен на каждую продукцию, при которых сохраняется оптимальный план.
- •10. На сколько нужно снизить затраты каждого вида сырья на единицу продукции, чтобы сделать производство нерентабельного изделия рентабельным?
- •11. На сколько нужно изменить запас каждого из дефицитных ресурсов, чтобы прибыль возросла на 20%?
- •3. Определите суммарную стоимостную оценку питательных веществ в единице каждого корма, использование какого вида корма нерентабельно.
- •Глава 4. Транспортная задача линейного программирования
- •0, Если безразлично, какой потребитель недополучит заявленного количества груза
- •4.3. Экономические задачи, сводящие к транспортной задаче.
- •Теорема о разрешимости транспортной задачи
- •4.4. Опорный план тз. Алгоритмы нахождения исходного плана.
- •4.4.1. Определения опорного плана тз.
- •4.4.2. Методы составления первоначальных опорных планов
- •4.5. Метод потенциалов решения транспортной задачи
- •4.6. Задача о назначениях
- •Глава 5. Задача целочисленного линейного программирования
- •5.1.Постановки и методы решения
- •5.2.Метод ветвей и границ решения целочисленных задач линейного программирования (цзлп)
- •5.3. Задача Коммивояжера.
2.5. Симплекс-метод решения злп.
Пусть требуется решить задачу
(2.52)
(2.53.)
(2.54)
Так
как по доказанному выше решением задачи
(2.52.)-(2.54.) является опорный план
(неотрицательное базисное решение
системы линейных уравнений
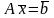 ),
то метод решения задачи должен содержать
четыре момента:
),
то метод решения задачи должен содержать
четыре момента:
обоснование способа перехода от одного опорного плана к другому;
указание признака оптимальности, позволяющего проверить, является ли данный опорный план оптимальным;
указание способа построения нового опорного плана, более близкого к оптимальному;
указание признака отсутствия конечного решения.
Определение к-матрицы кзлп
Определение 2.18. К-матрицей КЗЛП будем называть расширенную матрицу системы линейных уравнений, равносильной системе , содержащую единичную подматрицу на месте первых n своих столбцов и все элементы ( n+1 )-го столбца которой неотрицательны.
Теорема 2.17. Каждая К-матрица определяет опорный план КЗЛП и наоборот.
Доказательство теоремы очевидно.
Из
теоремы 2.11 следует, что число К-матриц
конечно и не превышает
![]() .
.
Пример 2.8. В примере 2.4 опорным планам:
соответствует
К-матрица
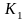 =
;
=
;
соответствует
К-матрица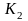 =
;
=
;
соответствует
К-матрица
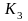 =
.
=
.
Переход от одной к-матрицы злп к другой к-матрице
Пусть известна К-матрица
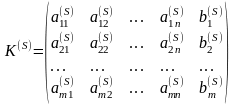 (2.55)
(2.55)
Обозначим
через
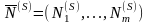 вектор номеров базисных (единичных)
столбцов матрицы
вектор номеров базисных (единичных)
столбцов матрицы
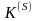 ,
,
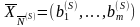 -вектор, компоненты которого есть
базисные компоненты опорного плана,
определяемого матрицей
,
и могут быть отличны от нуля. Остальные
(n-m)
компонент опорного плана, определяемого
матрицей
,
равны нулю. Очевидно, что векторы
-вектор, компоненты которого есть
базисные компоненты опорного плана,
определяемого матрицей
,
и могут быть отличны от нуля. Остальные
(n-m)
компонент опорного плана, определяемого
матрицей
,
равны нулю. Очевидно, что векторы
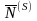 и
и
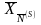 полностью
задают опорный план, определяемый
матрицей
.
Например, пусть
полностью
задают опорный план, определяемый
матрицей
.
Например, пусть
=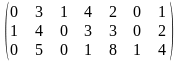 ,
,
тогда
=(
3,1,6);
=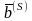 =(1,2,4)
и, следовательно, опорный план, определяемый
,
имеет вид
=(1,2,4)
и, следовательно, опорный план, определяемый
,
имеет вид
=(2,0,1,0,0,4).
Итак, пусть К-матрица (2.55) определяет невырожденный опорный план
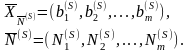 (2.56)
(2.56)
Выберем
в матрице
столбец
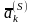 ,
не принадлежащий единичной подматрице,
т.е.
,
не принадлежащий единичной подматрице,
т.е.
 ,
,
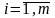 и такой, что в этом столбце есть хотя бы
один элемент больше нуля.
и такой, что в этом столбце есть хотя бы
один элемент больше нуля.
Пусть
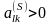 .
Считая
.
Считая
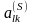 направляющим
элементом, совершим над матрицей
один шаг метода Жордана-Гаусса. В
результате получим новую матрицу
направляющим
элементом, совершим над матрицей
один шаг метода Жордана-Гаусса. В
результате получим новую матрицу
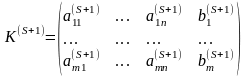 ,
(2.57)
,
(2.57)
элементы
которой выражаются через элементы
матрицы
следующим образом:
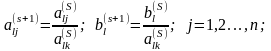 (2.58)
(2.58)
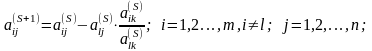 (2.59)
(2.59)
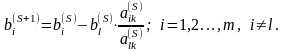 ,
(2.60)
,
(2.60)
в
которой столбец
стал единичным, но которая может и не
быть К-матрицей,
так как среди величин
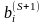 могут
быть отрицательные. Условия выбора
направляющего элемента
могут
быть отрицательные. Условия выбора
направляющего элемента
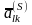 ,
позволяющие получить новую К-матрицу
-
,
позволяющие получить новую К-матрицу
-
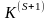 ,
т.е. обосновывающие способ перехода от
опорного плана
,
т.е. обосновывающие способ перехода от
опорного плана
![]() к
опорному плану
к
опорному плану
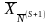 ,
составляет содержание следующей теоремы:
,
составляет содержание следующей теоремы:
Теорема 2.18. Пусть в k-м столбце К-матрицы - есть хотя бы один строго положительный элемент ( , ). Тогда с помощью одного шага метода Жордана-Гаусса можно построить новую К-матрицу - , выбрав направляющий элемент из условия:
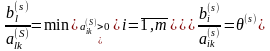 (2.61)
(2.61)
Доказательство.
Получим условия, которым должен удовлетворять направляющий элемент , чтобы
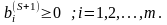
Из
соотношения
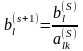 следует, что
следует, что
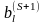 >0
>0
тогда и только тогда, когда
>0.
Это первое условие, которое мы должны наложить на выбор направляющего элемента.
Из
соотношения
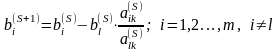 следует, что
следует, что
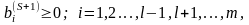
тогда и только тогда, когда
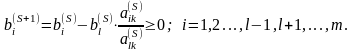 (1)
(1)
Это
условие выполняется для всех
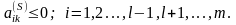
Перепишем
неравенство (1)
для строго положительных
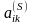 в виде
в виде
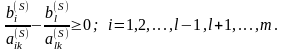 (2)
(2)
Очевидно,
что неравенство (2)
будет
выполняться для всех
>0,
если выбрать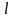 таким, что
таким, что
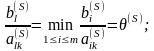 >0.
>0.
