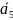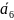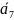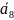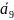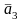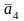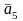- •Оглавление Введение. Экономика и математика Часть I. Линейные модели и методы в экономике.
- •Глава 1. Принятие решений в экономике
- •Глава 2. Линейное программирование. Теоретические основы и алгоритмы.
- •Глава 3. Теория двойственности в линейном программировании и ее экономические приложения.
- •Глава 4. Транспортная задача и ее приложения.
- •Глава 5. Задача целочисленного линейного программирования
- •Введение. Экономика и математика
- •Часть I. Линейные модели и методы в экономике.
- •Глава 1. Принятие решений в экономике.
- •1.1. Моделирование
- •1.2. Математическое моделирование.
- •1.3. Алгоритм исследования операции.
- •Алгоритм исследования операций.
- •1.4. Примеры исследования операции (моделирование)
- •1.5.Классификация моделей и методов исследования операций
- •Глава 2.
- •2.1. Постановки задачи линейного программирования
- •Основная задача линейного программирования (ОснЗлп)
- •Каноническая задача линейного программирования (кзлп)
- •2.2. Выпуклые множества.
- •0Пределение 2.4.
- •2.3. Теоретические основы линейного программирования
- •2.4. Графический метод и анализ решения злп
- •Проведем графический анализ решения (модели) на чувствительность.
- •2.5. Симплекс-метод решения злп.
- •Определение к-матрицы кзлп
- •Переход от одной к-матрицы злп к другой к-матрице
- •Симплекс-разность к-матрицы злп
- •Алгоритм симплекс-метода
- •2.6. Двойственный сиплекс-метод (р-метод)
- •Определение р-матрицы злп
- •Условия перехода от одной р-матрицы злп к другой
- •Решение задач р-методом
- •2.7.Метод искусственного базиса Назначение и принцип работы методов искусственного базиса
- •2.8. Модифицированный симплекс-метод Постановка задачи
- •Алгоритм модифицированного симплекс-метода
- •Решение задачи модифицированным симплекс-методом
- •2.9. Решение злп на основе Ms Excel
- •Глава 3. Теория двойственности в линейном программировании и ее экономические приложения.
- •3.1. Определение двойственной задачи:
- •3.2. Основные теоремы двойственности
- •3. 3. Экономическая интерпретация двойственности
- •Экономическое содержание теории двойственности.
- •3.4.Применение теории двойственности к решению задач. Применение теоремы 3.5 к решению дз.
- •3.5. Анализ решения злп на основе отчетов ms excel
- •2. Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов.
- •3. Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального плана, то есть номенклатура выпускаемой продукции, остается без изменения.
- •4. Определите суммарную стоимостную оценку ресурсов (себестоимость), используемых при производстве единицы каждого изделия. Производство какой продукции нерентабельно?
- •5. На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции?
- •6. На сколько можно снизить запас каждого из ресурсов, чтобы это не привело к уменьшению прибыли?
- •8. Определите оптимальное решение задачи для случая, когда вектор ресурсов задан в виде .
- •9. Определите интервалы изменения цен на каждую продукцию, при которых сохраняется оптимальный план.
- •10. На сколько нужно снизить затраты каждого вида сырья на единицу продукции, чтобы сделать производство нерентабельного изделия рентабельным?
- •11. На сколько нужно изменить запас каждого из дефицитных ресурсов, чтобы прибыль возросла на 20%?
- •3. Определите суммарную стоимостную оценку питательных веществ в единице каждого корма, использование какого вида корма нерентабельно.
- •Глава 4. Транспортная задача линейного программирования
- •0, Если безразлично, какой потребитель недополучит заявленного количества груза
- •4.3. Экономические задачи, сводящие к транспортной задаче.
- •Теорема о разрешимости транспортной задачи
- •4.4. Опорный план тз. Алгоритмы нахождения исходного плана.
- •4.4.1. Определения опорного плана тз.
- •4.4.2. Методы составления первоначальных опорных планов
- •4.5. Метод потенциалов решения транспортной задачи
- •4.6. Задача о назначениях
- •Глава 5. Задача целочисленного линейного программирования
- •5.1.Постановки и методы решения
- •5.2.Метод ветвей и границ решения целочисленных задач линейного программирования (цзлп)
- •5.3. Задача Коммивояжера.
2.7.Метод искусственного базиса Назначение и принцип работы методов искусственного базиса
Методы искусственного базиса предназначены для решения задач линейного программирования, содержащих ограничения различных видов: «больше
или равно », «меньше или равно », «равно ». При решении задачи линейного программирования для построения начального опорного плана необходимо,
чтобы в каждом ограничении присутствовала базисная переменная, т.е. переменная, входящая в данное ограничение с коэффициентом, равным
единице, и не входящая ни в одно из других ограничений.
В ограничениях «меньше или равно» в качестве таких переменных используются остаточные переменные, добавляемые в ограничение при его приведении к стандартной форме. Для приведения к стандартной форме ограничений «больше или равно » вводятся избыточные переменные
со знаком «минус ». В ограничения «равно » не требуется вводить никаких дополнительных переменных , так как такие ограничения уже соответствуют стандартной форме. Поэтому в задачах, содержащих ограничения «больше или равно » или «равно », после приведения к стандартной форме обычно невозможно построить начальный опорный план, так как базисные переменные имеются не во всех ограничениях. Для задач, содержащих ограничения «не меньше » или «равно», обычно нельзя использовать в качестве
начального
допустимого решения начало координат,
т. е. решение, в котором все исходные
переменные математической модели равны
нулю:
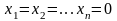 .
.
Такое решение, как правило, оказывается недопустимым (не соответствует ограничениям). Методы искусственного базиса применяются во всех
случаях, когда базисные переменные имеются не во всех ограничениях задачи, приведенной к стандартной форме. Принцип работы всех методов искусственного базиса следующий. Во все ограничения, не содержащие базисных переменных, вводятся искусственные переменные (по
одной в каждое ограничение ), используемые для построения начального базиса. После этого выполняется поиск оптимального решения на основе
обычных процедур симплекс - метода. В окончательном (оптимальном) решении задачи все искусственные переменные должны быть равны
нулю. Если в оптимальном решении какая - либо из искусственных переменных оказывается ненулевой, это означает, что задача не имеет допустимых решений. Причиной может быть ошибка в математической модели или противоречия в постановке задачи (например, количество изделий, которое требуется выпустить, не может быть выпущено из - за ограничений на ресурсы). На искусственные переменные, как и на все остальные переменные в задаче, накладывается требование неотрицательности. Искусственные переменные не имеют никакого физического смысла: их нельзя интерпретировать как количество изделий, запасы ресурсов и т. д. Они требуются только для построения начального базиса. Основные методы искусственного базиса – двухэтапный метод, рассматриваемый ниже, и метод больших штрафов. Поиск решения на основе этих методов выполняется с использованием симплекс – таблиц.
Рассмотрим общий метод отыскания опорного плана (или исходной K-матрицы) основной задачи линейного программирования – метод искусственного базиса.
Идея метода состоит в том, что наряду с исходной (2.52)-(2.54) задачей линейного программирования рассматривается следующая вспомогательная задача линейного программирования:
найти
вектор
 пространства
пространства
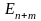 ,
максимизирующий линейную форму
,
максимизирующий линейную форму
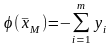 (2.85)
(2.85)
при условиях
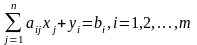 (2.86)
(2.86)
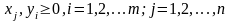 (2.87)
(2.87)
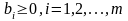 (2.88)
(2.88)
Переменные
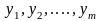
Будем называть искусственными переменными вспомогательной задачи линейного программирования в отличие от основных переменных
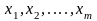
задачи.
Обозначим
PM - множество всех планов вспомогательной задачи линейного программирования;
P´M - множество тех планов вспомогательной задачи линейного программирования, все искусственные компоненты которых, являющиеся значениями искусственных переменных
равны нулю.
Очевидно,
между множествами PM
и P´M
существует
взаимно-однозначное соответствие и
если вектор
 является
планом вспомогательной задачи линейного
программирования, то вектор
является
планом вспомогательной задачи линейного
программирования, то вектор
 есть соответствующий ему план основной
задачи, и наоборот.
есть соответствующий ему план основной
задачи, и наоборот.
Так
как линейная форма
 ограничена сверху нулем на непустом
множестве PM
, то конечное
решение вспомогательной задачи линейного
программирования существует, а в силу
того, что расширенная матрица
ограничена сверху нулем на непустом
множестве PM
, то конечное
решение вспомогательной задачи линейного
программирования существует, а в силу
того, что расширенная матрица
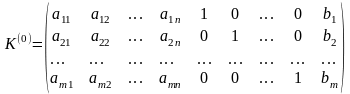
системы
линейных уравнений (2.86) является
K-матрицей
вспомогательной задачи, определяющей
ее исходный опорный план, это решение
можно в принципе найти симплексным
методом. Предположим, что вспомогательная
задача линейного программирования
решена симплексным методом, на S
– й итерации которого получен ее
оптимальный опорный план:
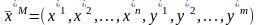 определяемый K
– матрицей.
определяемый K
– матрицей.
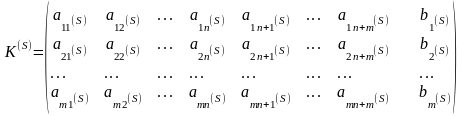 .
.
При этом матрица
 (2.89)
(2.89)
является расширенной матрицей системы линейных уравнений, равносильной системе (2.86)
Теорема 2.24.
Если
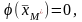 то вектор
является опорным планом основной задачи
линейного программирования. Если
то вектор
является опорным планом основной задачи
линейного программирования. Если
 <0,
то множество планов P
основной задачи линейного программирования
пусто.
<0,
то множество планов P
основной задачи линейного программирования
пусто.
Доказательство.
Пусть
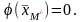
Это означает, что все искусственные компоненты оптимального опорного
плана
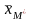 вспомогательной задачи линейного
программирования равны нулю,
вспомогательной задачи линейного
программирования равны нулю,
т.е.
 (2.90)
(2.90)
и вектор принадлежит множеству P´M .
Но тогда вектор является планом основной задачи линейного программирования, множество P´ не пусто и, следовательно, основная задача имеет хотя бы один опорный план.
При этом в процессе решения вспомогательной задачи симплексным методом могут представиться следующие два случая:
На S – й итерации симплексного метода ни одна из искусственных переменных не является базисной, т.е.
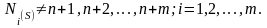 Тогда матрица (2.89) является K
– матрицей основной задачи линейного
программирования, а план
-
опорным планом основной задачи,
определяемым этой K-матрицей.
Тогда матрица (2.89) является K
– матрицей основной задачи линейного
программирования, а план
-
опорным планом основной задачи,
определяемым этой K-матрицей.На S – й итерации симплексного метода в числе базисных оказались искусственные переменные, например,
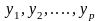
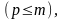
т.е.
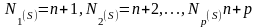
Тогда в силу равенства (2.90) p базисных компонент вектора равны нулю:
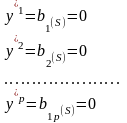
и,
следовательно, он является вырожденным
оптимальным опорным планом вспомогательной
задачи линейного программирования, а
матрица
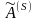 содержит p<m
единичных
столбцов и не является K
– матрицей основной задачи.
содержит p<m
единичных
столбцов и не является K
– матрицей основной задачи.
Однако в этом случае матрицу можно преобразовать в K – матрицу основной задачи линейного программирования, определяющую ее исходный опорный план .
Для этой цели рассмотрим любую r - ю строку из первых p строк матрицы (r = 1,2,…,p) .
Среди
элементов
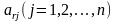 этой строки есть хотя бы один элемент,
отличный от нуля, так как в противном
случае ранг матрицы A
меньше m.
этой строки есть хотя бы один элемент,
отличный от нуля, так как в противном
случае ранг матрицы A
меньше m.
Выберем
этот элемент в качестве направляющего
и совершим один шаг метода Жордана –
Гаусса преобразования матрицы
с выбранным направляющим элементом. В
результате базисная искусственная
переменная
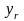 будет заменена одной из основных
переменных
будет заменена одной из основных
переменных
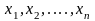 ,
а элементы (n+1)
– го столбца матрицы не изменятся.
,
а элементы (n+1)
– го столбца матрицы не изменятся.
После
p
таких шагов метода Жордана – Гаусса
матрица
будет преобразована в K-
матрицу основной задачи линейного
программирования, определяющую ее
исходный опорный план
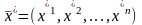 .
.
Очевидно, что этот опорный план будет вырожденным.
Пусть теперь <0, т.е. при решении вспомогательной задачи линейного программирования на S – й итерации симплексного метода в числе базисных оказались искусственные переменные, причем компоненты опорного плана , являющиеся значениями этих переменных, не равны нулю.
Предположим,
что в рассматриваемом случае множество
планов P´
основной задачи линейного программирования
не пусто и существует вектор
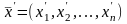 который
который
удовлетворяет ограничениям (2.86)-(2.88).
Но
тогда вектор
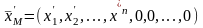 - план вспомогательной задачи линейного
программирования и такой, что
- план вспомогательной задачи линейного
программирования и такой, что
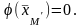
Следовательно,
<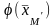 ,
а это противоречит предложению об
оптимальности вектора
.
,
а это противоречит предложению об
оптимальности вектора
.
Таким образом, решая вспомогательную задачу линейного программирования симплекс-методом, мы либо находим исходный опорный план основной задачи, либо убеждаемся, что множество планов P´ основной задачи линейного программирования пусто. После того, как найден исходный опорный план задачи линейного программирования, ее можно в принципе решать симплексным методом, т.е. практически решение основной задачи осуществляется в два этапа.
Пример 2.13. Рассмотрим задачу
=0.4X1+0.3X2+0.1X3+0.1X5+0.2X6 (1)
2X2+2X3+4X4+X5=150
X1+X2+2X5=200 (2)
X1+X3+2X6=300
![]() ;
j=1,...,6 (3)
;
j=1,...,6 (3)
Так
как ограничения (2) рассматриваемой ЗЛП
уже имеют вид строгих равенств, то для
приведения ее к каноническому виду
достаточно только изменить знак функции
на
противоположный и рассмотреть задачу
нахождения
![]() -0.4X1-0.3X2-0.1X3-0.1X5-0.2X6
(4) при тех же ограничениях (3.2)-(3).
-0.4X1-0.3X2-0.1X3-0.1X5-0.2X6
(4) при тех же ограничениях (3.2)-(3).
Рассмотрим расширенную матрицу системы уравнений (2)

Так как расширенная матрица не содержит единичной подматрицы порядка 3,то она не является К-матрицей ЗЛП и, следовательно, к задаче (2)-(4) не может быть применен симплекс-метод.
Рассмотрим метод отыскания исходного опорного плана (К-матрицы)- метод искусcтвенного базиса.
Для задачи (2)-(4) запишем ВЗ:
![]() -(U1+U2+U3)
-(U1+U2+U3)
![]() max
(5)
max
(5)
2X1+2X3+4X4+X5+U1=150
X1+X2+2X5+U2=200 (6)
X1+X3+2X6+U3=300
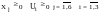 (7)
(7)
Результаты первого этапа представлены в табл. 2.7
Таблица 2.7
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
-1 |
|
|
|
S |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
7 |
-1 |
150 |
0 |
2 |
2 |
4 |
1 |
0 |
1 |
0 |
0 |
|
37.5 |
|
0 |
2 |
8 |
-1 |
200 |
1 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
|
- |
|
|
3 |
9 |
-1 |
300 |
1 |
0 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
|
- |
|
|
4 |
|
|
-650 |
-2 |
-3 |
-3 |
-4 |
-3 |
-2 |
0 |
0 |
0 |
|
|
|
|
1 |
4 |
0 |
37.5 |
0 |
0.5 |
0.5 |
1 |
0.25 |
0 |
0.25 |
0 |
0 |
- |
150 |
- |
1 |
2 |
8 |
-1 |
200 |
1 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
200 |
100 |
- |
|
3 |
9 |
-1 |
300 |
1 |
0 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
300 |
- |
150 |
|
4 |
|
|
-500 |
-2 |
-1 |
-1 |
0 |
-2 |
-2 |
1 |
0 |
0 |
|
|
|
|
1 |
4 |
0 |
37.5 |
0 |
0.5 |
0.5 |
1 |
0.25 |
0 |
0.25 |
0 |
0 |
|
- |
|
2 |
2 |
1 |
0 |
200 |
1 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
|
- |
|
|
3 |
9 |
-1 |
100 |
0 |
-1 |
1 |
0 |
-2 |
2 |
0 |
-1 |
1 |
|
50 |
|
|
4 |
|
|
-100 |
0 |
1 |
-1 |
0 |
2 |
-2 |
1 |
2 |
0 |
|
|
|
|
1 |
4 |
0 |
37.5 |
0 |
0.5 |
0.5 |
1 |
0.25 |
0 |
0.25 |
0 |
0 |
|
|
|
3 |
2 |
1 |
0 |
200 |
1 |
1 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
|
|
|
|
3 |
6 |
0 |
50 |
0 |
-0.5 |
0.5 |
0 |
-1 |
1 |
0 |
-0.5 |
0.5 |
|
|
|
|
4 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
|
На
третьей итерации симплексного метода
получен оптимальный план вспомогательной
задачи:
![]() =(200;
0; 0; 37.5; 0; 50; 0; 0; 0),
=(200;
0; 0; 37.5; 0; 50; 0; 0; 0),
в
котором ни одна из искусственных
переменных не является базисной,
следовательно, вектор
![]() =(200;
0; 0; 37.5; 0; 50) является невырожденным
опорным планом исходной задачи,
определяемым К-матрицей.
=(200;
0; 0; 37.5; 0; 50) является невырожденным
опорным планом исходной задачи,
определяемым К-матрицей.

На втором этапе решаем задачу
max(-0.4X1-0.3X2-0.1X3-0.1X5-0.2X6)
![]() .
.
Решение приведено в табл. 2.8.
Таблица 2.8.
|
|
|
|
|
-0.4 |
-0.3 |
-0.1 |
0 |
-0.1 |
-0.2 |
|
S |
i |
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
0 |
37.5 |
0 |
0.5 |
0.5 |
1 |
0.25 |
0 |
150 |
0 |
2 |
1 |
-0.4 |
200 |
1 |
1 |
0 |
0 |
2 |
0 |
100 |
|
3 |
6 |
-0.2 |
50 |
0 |
-0.5 |
0.5 |
0 |
-1 |
1 |
- |
|
4 |
|
|
-90 |
0 |
0 |
0 |
0 |
-0.5 |
0 |
|
|
1 |
4 |
0 |
12.5 |
-0.125 |
0.375 |
0.5 |
1 |
0 |
0 |
25 |
1 |
2 |
5 |
-0.1 |
100 |
0.5 |
0.5 |
0 |
0 |
1 |
0 |
- |
|
3 |
6 |
-0.2 |
150 |
1 |
0 |
1 |
0 |
0 |
1 |
300 |
|
4 |
|
|
-40 |
0.25 |
0.25 |
0 |
0 |
0 |
0 |
|
|
1 |
3 |
-0.1 |
25 |
-0.25 |
0.75 |
1 |
2 |
0 |
0 |
|
2 |
2 |
5 |
-0.1 |
100 |
0.5 |
1 |
0 |
0 |
1 |
0 |
|
|
3 |
6 |
-0.2 |
137.5 |
0.625 |
-0.375 |
0 |
-1 |
0 |
1 |
|
|
4 |
|
|
-40 |
0.25 |
0.25 |
0 |
0 |
0 |
0 |
|
На
первой итерации (табл. 2.8.) второго этапа
получен оптимальный план исходной
задачи
1=(0;
0; 12.5; 100; 150) и
![]() =40.
=40.
Так
как
![]() =0,
а вектор
=0,
а вектор
![]() не является базисным, то его можно ввести
в базис, и при этом в соответствии с
формулой (3.28) значение целевой функции
не изменится, т.е. на второй итерации
можно получить еще один оптимальный
план исходной задачи
не является базисным, то его можно ввести
в базис, и при этом в соответствии с
формулой (3.28) значение целевой функции
не изменится, т.е. на второй итерации
можно получить еще один оптимальный
план исходной задачи
2=(0;
0.25; 0; 100; 137.5) и
![]() =40.
=40.
Исходная
задача имеет бесчисленное множество
решений, задаваемое формулой
![]() (8)
(8)
Пример 2.14. Решить ЗЛП:
max(2X1-X2-X4)
X1-2X2+X3=10
-2X1-X2-2X4 18 (9)
3X1+2X2+X4 36

Приведем ЗЛП (9) к каноническому виду
max(2X1-X2-X4)
X1-2X2+X3=10
-2X1-X2-2X4- S1 =18 (10)
3X1+2X2+X4-S2 =36
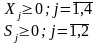
Расширенная матрица системы линейных уравнений (10)
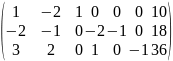
не является К-матрицей ЗЛП (10), т.к. не содержит единичной подматрицы.
Запишем
вспомогательную задачу для ЗЛП (10). Т.к.
матрица
![]() содержит
один единичный вектор
=(1;
0; 0), то при формулировке ВЗ достаточно
ввести лишь две искусственные переменные
U1;U2
во второе и третье уравнения системы
(10).
содержит
один единичный вектор
=(1;
0; 0), то при формулировке ВЗ достаточно
ввести лишь две искусственные переменные
U1;U2
во второе и третье уравнения системы
(10).
Итак, ВЗ имеет вид
-(U1+U2) max
X1-2X2+X3=10
-2X1-X2-2X4-X5+U1=18 (11)
3X1+2X2+X4-X6+U2=36
![]() ;
U1
,U2
0
;
U1
,U2
0
Решение ВЗ приведено в табл 2.9.
Таблица 2.9
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
|
S |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
0 |
10 |
-1 |
-2 |
1 |
0 |
0 |
0 |
0 |
0 |
- |
0 |
2 |
7 |
-1 |
18 |
-2 |
-1 |
0 |
-2 |
-1 |
0 |
1 |
0 |
- |
|
3 |
8 |
-1 |
36 |
3 |
2 |
0 |
1 |
0 |
-1 |
0 |
1 |
18 |
|
4 |
|
|
-54 |
-1 |
-1 |
0 |
1 |
1 |
1 |
0 |
0 |
|
|
1 |
3 |
0 |
46 |
2 |
0 |
1 |
1 |
0 |
-1 |
0 |
1 |
|
1 |
2 |
7 |
-1 |
36 |
-0.5 |
0 |
0 |
-1.5 |
-1 |
-0.5 |
1 |
0.5 |
|
|
3 |
2 |
0 |
18 |
1.5 |
1 |
0 |
0.5 |
0 |
-0.5 |
0 |
0.5 |
|
|
4 |
|
|
-36 |
0.5 |
0 |
0 |
1.5 |
1 |
0.5 |
0 |
0.5 |
|
На первой итерации получен оптимальный план.
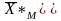 =(
0; 18; 46; 0; 0; 36; 0 ).
=(
0; 18; 46; 0; 0; 36; 0 ).
Т.к. вектор имеет отличную от нуля искусственную переменную U1=36, то множество планов ЗЛП (9 ) пусто в силу несовместности системы уравнений (10).