
- •Оглавление Введение. Экономика и математика Часть I. Линейные модели и методы в экономике.
- •Глава 1. Принятие решений в экономике
- •Глава 2. Линейное программирование. Теоретические основы и алгоритмы.
- •Глава 3. Теория двойственности в линейном программировании и ее экономические приложения.
- •Глава 4. Транспортная задача и ее приложения.
- •Глава 5. Задача целочисленного линейного программирования
- •Введение. Экономика и математика
- •Часть I. Линейные модели и методы в экономике.
- •Глава 1. Принятие решений в экономике.
- •1.1. Моделирование
- •1.2. Математическое моделирование.
- •1.3. Алгоритм исследования операции.
- •Алгоритм исследования операций.
- •1.4. Примеры исследования операции (моделирование)
- •1.5.Классификация моделей и методов исследования операций
- •Глава 2.
- •2.1. Постановки задачи линейного программирования
- •Основная задача линейного программирования (ОснЗлп)
- •Каноническая задача линейного программирования (кзлп)
- •2.2. Выпуклые множества.
- •0Пределение 2.4.
- •2.3. Теоретические основы линейного программирования
- •2.4. Графический метод и анализ решения злп
- •Проведем графический анализ решения (модели) на чувствительность.
- •2.5. Симплекс-метод решения злп.
- •Определение к-матрицы кзлп
- •Переход от одной к-матрицы злп к другой к-матрице
- •Симплекс-разность к-матрицы злп
- •Алгоритм симплекс-метода
- •2.6. Двойственный сиплекс-метод (р-метод)
- •Определение р-матрицы злп
- •Условия перехода от одной р-матрицы злп к другой
- •Решение задач р-методом
- •2.7.Метод искусственного базиса Назначение и принцип работы методов искусственного базиса
- •2.8. Модифицированный симплекс-метод Постановка задачи
- •Алгоритм модифицированного симплекс-метода
- •Решение задачи модифицированным симплекс-методом
- •2.9. Решение злп на основе Ms Excel
- •Глава 3. Теория двойственности в линейном программировании и ее экономические приложения.
- •3.1. Определение двойственной задачи:
- •3.2. Основные теоремы двойственности
- •3. 3. Экономическая интерпретация двойственности
- •Экономическое содержание теории двойственности.
- •3.4.Применение теории двойственности к решению задач. Применение теоремы 3.5 к решению дз.
- •3.5. Анализ решения злп на основе отчетов ms excel
- •2. Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов.
- •3. Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального плана, то есть номенклатура выпускаемой продукции, остается без изменения.
- •4. Определите суммарную стоимостную оценку ресурсов (себестоимость), используемых при производстве единицы каждого изделия. Производство какой продукции нерентабельно?
- •5. На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции?
- •6. На сколько можно снизить запас каждого из ресурсов, чтобы это не привело к уменьшению прибыли?
- •8. Определите оптимальное решение задачи для случая, когда вектор ресурсов задан в виде .
- •9. Определите интервалы изменения цен на каждую продукцию, при которых сохраняется оптимальный план.
- •10. На сколько нужно снизить затраты каждого вида сырья на единицу продукции, чтобы сделать производство нерентабельного изделия рентабельным?
- •11. На сколько нужно изменить запас каждого из дефицитных ресурсов, чтобы прибыль возросла на 20%?
- •3. Определите суммарную стоимостную оценку питательных веществ в единице каждого корма, использование какого вида корма нерентабельно.
- •Глава 4. Транспортная задача линейного программирования
- •0, Если безразлично, какой потребитель недополучит заявленного количества груза
- •4.3. Экономические задачи, сводящие к транспортной задаче.
- •Теорема о разрешимости транспортной задачи
- •4.4. Опорный план тз. Алгоритмы нахождения исходного плана.
- •4.4.1. Определения опорного плана тз.
- •4.4.2. Методы составления первоначальных опорных планов
- •4.5. Метод потенциалов решения транспортной задачи
- •4.6. Задача о назначениях
- •Глава 5. Задача целочисленного линейного программирования
- •5.1.Постановки и методы решения
- •5.2.Метод ветвей и границ решения целочисленных задач линейного программирования (цзлп)
- •5.3. Задача Коммивояжера.
Глава 3. Теория двойственности в линейном программировании и ее экономические приложения.
3.1. Определение двойственной задачи:
Двойственная задача- это вспомогательная задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной или прямой задачи. Часто рассматриваются формулировки двойственной задачи (ДЗ), соответствующие различным формам записи исходной задачи (ИЗ). Поскольку использование симплексного и других методов решения ЗЛП требует приведения ЗЛП к каноническому виду, сформулируем определение ДЗ к ИЗ, записанной в каноническом виде.
Исходная задача
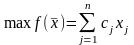 (3.1)
(3.1)
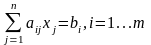 (3.2)
(3.2)
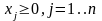 (3.3)
(3.3)
Задачей, двойственной к ЗЛП (3.1)-(3.3), назовем следующую ЗЛП:
Двойственная задача
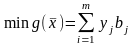 (3.4)
(3.4)
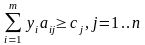 (3.5)
(3.5)
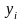 не
ограничен в знаке,
не
ограничен в знаке,
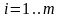 (3.6)
(3.6)
Двойственная ЗЛП строится по следующим правилам:
Каждому ограничению исходной задачи соответствует переменная двойственной задачи, т.е. число переменных двойственной задачи равно числу ограничений исходной задачи.
Каждой переменной исходной задачи соответствует ограничение двойственной задачи, т.е. число ограничений двойственной задачи равно числу переменных исходной задачи.
Матрица функциональных ограничений двойственной задачи получается путём транспонирования матрицы функциональных ограничений исходной задачи.
Вектор
 целевой функции
прямой задачи становится вектором
правой части ограничений двойственной
задачи, а вектор
целевой функции
прямой задачи становится вектором
правой части ограничений двойственной
задачи, а вектор
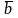 правой части прямой задачи – вектором
целевой функции двойственной задачи.
правой части прямой задачи – вектором
целевой функции двойственной задачи.Целевая функция исходной задачи максимизируется, целевая функция двойственной задачи минимизируется, а ограничения имеют вид больше либо равно.
Итак:
Исходная задача |
Двойственная задача |
|
|
P =
|
Q
=
|
(3.7) |
|
Пример 3.1. Пусть исходная задача имеет вид:
min
|
(3.8) |
Приведем
ее к каноническому виду, т.е. будем
максимизировать функцию
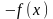 .
.
|
(3.9) |
По определению, задачей двойственной к (3.9), будет задача:
|
(3.10) |
Если обозначить через
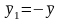 ,
то (3.10)
примет
вид:
,
то (3.10)
примет
вид:
|
(3.11) |
Из примера 3.1 следует, что если функция ИЗ минимизируется, то функция ДЗ максимизируется и ограничения меняют знак на противоположный (меньше либо равно).
Пример 3.2. Пусть ИЗ записана в виде основной ЗЛП:
|
(3.12) |
Приведем ограничения задачи (3.12) к канонической форме:
|
(3.13) |
Тогда ДЗ к основной ЗЛП будет иметь вид:
|
(3.14) |
Пара задач (3.12),(3.14) называется симметричной парой двойственных задач.
Пример 3.3.
Прямая задача:
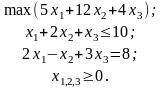
Прямая задача с ограничениями в канонической форме:
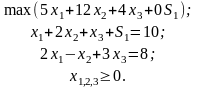
S1 ≥ 0
Двойственная задача:
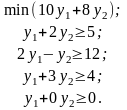
y1,2 не ограничены в знаке.
Ограничение
![]() ,
т.е.
,
т.е.
![]() ,
является более жестким, чем условие
неограниченности у1
в знаке, поэтому двойственная задача
может быть записана в следующем виде:
,
является более жестким, чем условие
неограниченности у1
в знаке, поэтому двойственная задача
может быть записана в следующем виде:
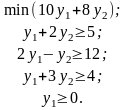
у2 не ограничена в знаке.
Если формулировать ДЗ к ИЗ, минуя ее приведение к КЗЛП, то на основании примера 3.3. можно сделать следующие выводы:
Если ограничение ИЗ является нестрогим, то соответствующая двойственная переменная ограничена в знаке;
Если ограничение ИЗ является строгим, то соответствующая двойственная переменная не ограничена в знаке.
Пример 3.4. Прямая задача:
min(5X1 – 2X2);
–X1 + X2 ≥ –3;
2X1 + 3X2 ≤ 5;
X1,2 ≥ 0.
Прямая задача с ограничениями в канонической форме:
min(5X1 – 2X2 + 0S1 + 0S2);
–X1 + X2 – S1 = –3;
2X1 + 3X2 + S2 = 5;
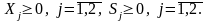
Двойственная задача:
max(–3У1 + 5У2);
–У1 + 2У2 ≤ 5;
У1 + 3У2 ≤ –2;
–У1 + 0У2 ≤ 0;
0У1 + У2 ≤ 0.
У1,2 не ограничены в знаке.
Отбрасывая избыточные ограничения, получаем:
max(–3У1 + 5У2);
–У1 + 2У2 ≤ 5;
У1 + 3У2 ≤ –2;
У1 ≥ 0, У2 ≤ 0.
Из решения примера 3.4 следует:
если в ИЗ ограничение является «неправильным» (в задаче на минимум - ≤, в задаче на максимум - ≥), то соответствующая двойственная переменная будет неположительной (У2 ≤ 0).
Пример 3.5. ИЗ:
max(5X1 + 6X2);
X1 + 2X2 = 5;
–X1 + 5X2 ≥ 3;
4X1 + 7X2 ≤ 8.
X1 не ограничена в знаке, X2 ≥ 0.
ИЗ в канонической форме:
max(5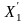 – 5
– 5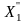 + 6X2
+ 0S1
+ 0S2);
+ 6X2
+ 0S1
+ 0S2);
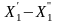 +
2X2
= 5;
+
2X2
= 5;
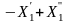 +
5X2
– S1
= 3;
+
5X2
– S1
= 3;
4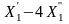 + 7X2
+ S2
= 8;
+ 7X2
+ S2
= 8;
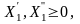
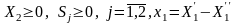
ДЗ:
min(5У1 + 3У2 + 8У3);
У1 – У2 + 4У3 ≥ 5;
–У1 + У2 – 4У3 ≥ –5;
2У1 + 5У2 + 7У3 ≥ 6;
0У1 – У2 + 0У3 ≥ 0;
0У1 + 0У2 + У3 ≥ 0.
У1,2,3 не ограничены в знаке.
Заметим, что первое и второе ограничения двойственной задачи можно заменить одним ограничением в виде равенства, избыточные ограничения на У2 и У3 можно отбросить. В итоге получаем:
min(5У1 + 3У2 + 8У3);
У1 – У2 + 4У3 = 5;
2У1 + 5У2 + 7У3 ≥ 6;
У1 не ограничена в знаке;
У2 ≤ 0, У3 ≥ 0.
Из решения примера 3.5 следует:
если переменная ИЗ не ограничена в знаке, то соответствующее ограничение ДЗ будет иметь вид строгого равенства.
Теорема 3.1.
Задача, двойственная к двойственной,
совпадает с исходной, т.е.
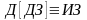 .
Доказательство очевидно.
.
Доказательство очевидно.
На основании выводов, сделанных при решении примеров 3.1.-3.5., можно формулировать общие правила построения ДЗ для ИЗ, записанной в произвольной форме.
Если целевая функция ИЗ максимизируется, то целевая функция ДЗ минимизируется, и наоборот.
Если в ИЗ на максимум (минимум) i-е ограничение имеет вид ≥(≤) («неправильное»), то в ДЗ i-я переменная будет неположительной.
Если i-е ограничение ИЗ имеет вид строгого равенства, то i-я переменная ДЗ будет не ограничена в знаке.
Если в ИЗ j-я переменная не ограничена в знаке, то j-е ограничение ДЗ будет строгим равенством.

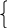
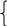 max
max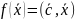
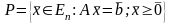 -
множество планов ИЗ
-
множество планов ИЗ

 – не ограничен в знаке
– не ограничен в знаке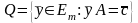 -
множество планов ДЗ
-
множество планов ДЗ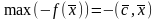
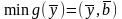
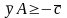 ,
не ограничен в знаке
,
не ограничен в знаке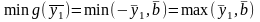
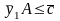 ,
,
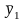 не ограничен в знаке.
не ограничен в знаке.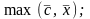
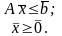
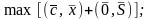
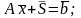
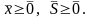
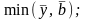
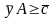
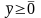 .
.