Симплекс-разность к-матрицы злп

Определение 2.19. Величину

,

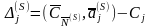где 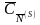- вектор, компонентами которого являются коэффициенты линейной функции при базисных ( ) переменных опорного плана, определяемого матрицей , назовем j-й симплекс-разностью матрицы .

Если столбец 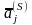является единичным в матрице , то 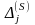=0

Посмотрим, как изменяется j-я симплекс - разность при переходе от K-матрицы к новой K- матрице ЗЛП. Согласно определению симплекс – разности имеем

.

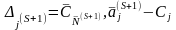Используя в этом соотношении формулы

(1)

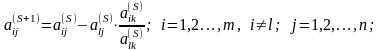(2)

, (3)

найдем

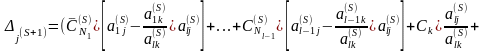
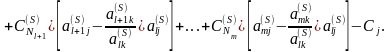
Сложим последнее равенство с тождеством

в результате получим

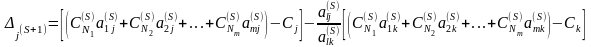
или окончательно

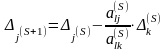. (2.62)

Изменение функции цели ЗЛП при переходе от одной К-матрицы к другой

Пусть и - опорные планы, определяемые матрицами и соответственно.

Тогда очевидно, что

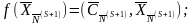
_(2.63)

Посмотрим, как изменяется функция цели 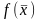при переходе от K-матрицы к новой K- матрице задачи линейного программирования. Имеем

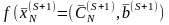
Используя в этом соотношении формулы (1)-(3), найдем

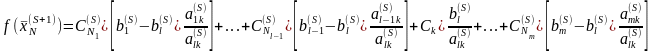Сложим это равенство с тождеством

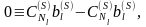
в результате получим

или в векторной форме

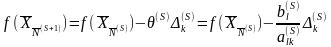, (2.64)

где k - номер столбца , вводимого в базис при получении матрицы из . определяется по формуле (2.61).

Теорема 2.19 Пусть в матрице есть 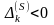и в столбце ( , ) есть хотя бы один строго положительный элемент. Тогда от матрицы можно перейти к матрице , причем

f ( ) f( ). (2.65)

Доказательство.

Так как в столбце матрицы есть строго положительный элемент, то согласно теореме 2.18 от матрицы можно перейти к новой матрице ЗЛП, выбрав направляющий элемент из условия (2.61).

_{Неравенство (2.65) вытекает из выражения (2.64), так как} , а _0.

_{Теорема 2.20. (критерий оптимальности опорного плана) Пусть все симплекс-разности матрицы} неотрицательные. Тогда опорный план , определяемый матрицей , является оптимальным.

Доказательство.

По условию теоремы

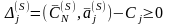
или

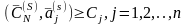(2.66)

Пусть - произвольный план ЗЛП. Умножим левую и правую части (2.66) на 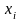, тогда в силу неотрицательности получим

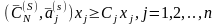(2.67)

Согласно (2.67) имеем

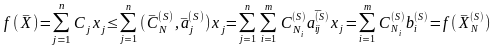
или

,

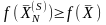что и доказывает теорему.

Теорема 2.21. Пусть в матрице есть , и в столбце ( , ) нет ни одного строго положительного элемента. Тогда ЗЛП (2.52)-(2.54) не имеет конечного решения.

Доказательство.

Пусть k-я симплекс-разность матрицы

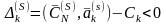, (2.68)

и все

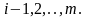(2.69)

Матрица определяет опорный план

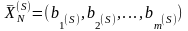
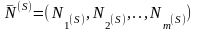
Рассмотрим вектор

,

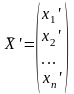у которого

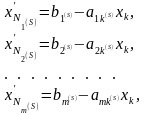
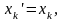
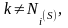
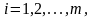
где 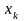- любое положительное число.

Остальные 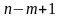компонент вектора положим равными нулю.

В силу условия (2.69) компоненты вектора неотрицательные. Легко убедиться в том, что компоненты вектора удовлетворяют и функциональным ограничениям (2.53) ЗЛП, т.е. вектор - план ЗЛП при любом положительном .

Имеем:

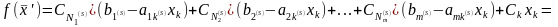
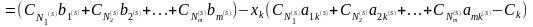
или окончательно

(2.70)

Так как , то из (2.70) следует, что для любого числа 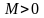всегда можно найти план ЗЛП, для которого

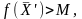
т.е. линейная форма 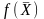не ограничена сверху на множестве планов .
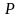