
- •Оглавление Введение. Экономика и математика Часть I. Линейные модели и методы в экономике.
- •Глава 1. Принятие решений в экономике
- •Глава 2. Линейное программирование. Теоретические основы и алгоритмы.
- •Глава 3. Теория двойственности в линейном программировании и ее экономические приложения.
- •Глава 4. Транспортная задача и ее приложения.
- •Глава 5. Задача целочисленного линейного программирования
- •Введение. Экономика и математика
- •Часть I. Линейные модели и методы в экономике.
- •Глава 1. Принятие решений в экономике.
- •1.1. Моделирование
- •1.2. Математическое моделирование.
- •1.3. Алгоритм исследования операции.
- •Алгоритм исследования операций.
- •1.4. Примеры исследования операции (моделирование)
- •1.5.Классификация моделей и методов исследования операций
- •Глава 2.
- •2.1. Постановки задачи линейного программирования
- •Основная задача линейного программирования (ОснЗлп)
- •Каноническая задача линейного программирования (кзлп)
- •2.2. Выпуклые множества.
- •0Пределение 2.4.
- •2.3. Теоретические основы линейного программирования
- •2.4. Графический метод и анализ решения злп
- •Проведем графический анализ решения (модели) на чувствительность.
- •2.5. Симплекс-метод решения злп.
- •Определение к-матрицы кзлп
- •Переход от одной к-матрицы злп к другой к-матрице
- •Симплекс-разность к-матрицы злп
- •Алгоритм симплекс-метода
- •2.6. Двойственный сиплекс-метод (р-метод)
- •Определение р-матрицы злп
- •Условия перехода от одной р-матрицы злп к другой
- •Решение задач р-методом
- •2.7.Метод искусственного базиса Назначение и принцип работы методов искусственного базиса
- •2.8. Модифицированный симплекс-метод Постановка задачи
- •Алгоритм модифицированного симплекс-метода
- •Решение задачи модифицированным симплекс-методом
- •2.9. Решение злп на основе Ms Excel
- •Глава 3. Теория двойственности в линейном программировании и ее экономические приложения.
- •3.1. Определение двойственной задачи:
- •3.2. Основные теоремы двойственности
- •3. 3. Экономическая интерпретация двойственности
- •Экономическое содержание теории двойственности.
- •3.4.Применение теории двойственности к решению задач. Применение теоремы 3.5 к решению дз.
- •3.5. Анализ решения злп на основе отчетов ms excel
- •2. Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов.
- •3. Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального плана, то есть номенклатура выпускаемой продукции, остается без изменения.
- •4. Определите суммарную стоимостную оценку ресурсов (себестоимость), используемых при производстве единицы каждого изделия. Производство какой продукции нерентабельно?
- •5. На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции?
- •6. На сколько можно снизить запас каждого из ресурсов, чтобы это не привело к уменьшению прибыли?
- •8. Определите оптимальное решение задачи для случая, когда вектор ресурсов задан в виде .
- •9. Определите интервалы изменения цен на каждую продукцию, при которых сохраняется оптимальный план.
- •10. На сколько нужно снизить затраты каждого вида сырья на единицу продукции, чтобы сделать производство нерентабельного изделия рентабельным?
- •11. На сколько нужно изменить запас каждого из дефицитных ресурсов, чтобы прибыль возросла на 20%?
- •3. Определите суммарную стоимостную оценку питательных веществ в единице каждого корма, использование какого вида корма нерентабельно.
- •Глава 4. Транспортная задача линейного программирования
- •0, Если безразлично, какой потребитель недополучит заявленного количества груза
- •4.3. Экономические задачи, сводящие к транспортной задаче.
- •Теорема о разрешимости транспортной задачи
- •4.4. Опорный план тз. Алгоритмы нахождения исходного плана.
- •4.4.1. Определения опорного плана тз.
- •4.4.2. Методы составления первоначальных опорных планов
- •4.5. Метод потенциалов решения транспортной задачи
- •4.6. Задача о назначениях
- •Глава 5. Задача целочисленного линейного программирования
- •5.1.Постановки и методы решения
- •5.2.Метод ветвей и границ решения целочисленных задач линейного программирования (цзлп)
- •5.3. Задача Коммивояжера.
3.2. Основные теоремы двойственности
Рассмотрим не симметричную пару двойственных задач (3.7).
Прямая задача |
Двойственная задача |
(2) (3) |
(5) не ограничен в знаке (6)
|
Теорема 3.2.
Пусть
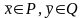 -
планы соответственно исходной и
двойственной ЗЛП,
-
планы соответственно исходной и
двойственной ЗЛП,
тогда
|
(3.15) |
Доказательство.
Умножим равенство (2) на
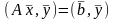
Умножим неравенство (5) на
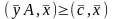 или
или
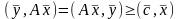
Откуда
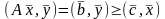 ,
т.е.
.
,
т.е.
.
Теорема 3.3.
Пусть
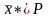 и
и
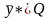 - планы соответственно исходной и
двойственной ЗЛП и
- планы соответственно исходной и
двойственной ЗЛП и
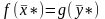 ,
,
тогда
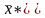 и
и
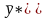 - решения соответственно исходной и
двойственной задач, т.е. равенство
целевых функций является достаточным
условием оптимальности планов обеих
задач.
- решения соответственно исходной и
двойственной задач, т.е. равенство
целевых функций является достаточным
условием оптимальности планов обеих
задач.
Доказательство.
Пусть
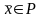 -произвольный
план ИЗ, тогда в силу предыдущей теоремы
для пары
-произвольный
план ИЗ, тогда в силу предыдущей теоремы
для пары
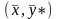 можно записать (3.15):
можно записать (3.15):
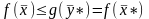
Следовательно:
 ,
т.е. по определению 2.2
есть решение ИЗ.
,
т.е. по определению 2.2
есть решение ИЗ.
Пусть
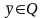 ,
тогда в силу предыдущей теоремы для
пары
,
тогда в силу предыдущей теоремы для
пары
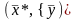
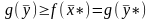
Следовательно,
 ,
т.е.
решение ДЗ
,
т.е.
решение ДЗ
Теорема 3.4.
Если ИЗ разрешима, то разрешима и ДЗ и наоборот, причем

Если ИЗ неразрешима, то ДЗ тоже неразрешима и наоборот. Пусть ИЗ разрешима и имеет вид основной ЗЛП:
(1)
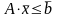 (2)
(2)
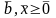 (3)
(3)
Тогда ДЗ имеет вид (3.12,3.14):
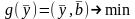 (4)
(4)
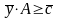 (5)
(5)
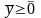 (6)
(6)
Предположим, что исходная задача имеет решение, т.е. существует ее оптимальный план x*.
Приведем ИЗ к каноническому виду:
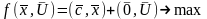 (1´)
(1´)
 (2´)
(2´)
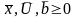 (3´)
(3´)
Ее
решение может быть получено симплекс
– методом, т.к. расширенная матрица
системы (2´) имеет вид К-матрицы.
Исходную
К-
матрицу
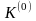 запишем в виде:
запишем в виде:
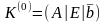 (7)
(7)
На S-ой итерации симплекс-метода получим матрицу , которая определяет оптимальный опорный план ИЗ:
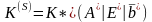 ,
(8)
,
(8)
или в развернутом виде эти матрицы можно представить:
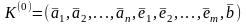 (7´)
(7´)
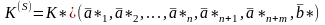 (8´)
(8´)
Вектор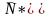 задает номера базисных компонент
оптимального опорного плана ИЗ:
задает номера базисных компонент
оптимального опорного плана ИЗ:
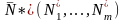
Векторы
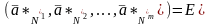 образуют
базисную (единичную) подматрицу в
матрице
,
следовательно, векторы
образуют
базисную (единичную) подматрицу в
матрице
,
следовательно, векторы
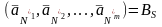 исходной матрицы
образуют базисную подматрицу
исходной матрицы
образуют базисную подматрицу
 в
матрице
,
т.е.
в
матрице
,
т.е.
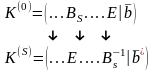
Следовательно,
матрицу
,
зная матрицу
,
можно получить из
следующим образом :
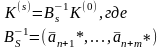 (9)
(9)
Матрица
в
матрице
расположена на месте единичной подматрицы
исходной матрицы
.
Из (9) следует, что
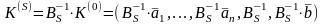 (3.16)
(3.16)
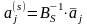 ,
,
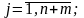 (3.17)
(3.17)
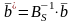 ,
(3.18)
,
(3.18)
т.е. вся необходимая информация может быть получена с помощью матрицы . Следовательно, можно перебирать не К-матрицы, а только обращенные базисы.
Так как на S-ой итерации получен оптимальный опорный план,
то отвечающие матрице симплекс – разности, являются неотрицательными
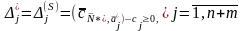 (3.19)
(3.19)
Или с учетом (3.17) получим:
 (3.20)
(3.20)
Обозначим
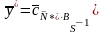 (3.21)
(3.21)
Покажем,
что вектор
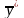 является
решением двойственной ЗЛП.
является
решением двойственной ЗЛП.
Действительно, рассматривая первые n неравенств (3.20) и записывая их в векторно-матричной форме, имеем:
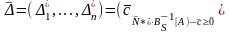 ,
или с учетом (3.21)
,
или с учетом (3.21)
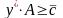 (3.22)
(3.22)
Аналогично, рассматривая неравенства (3.20) для j=n+1,n+m и учитывая, что
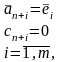
получаем
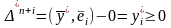 (3.23)
(3.23)
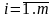 ,
,
или
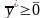 (3.24)
(3.24)
Из (3.22) и (3.24) следует, что - план двойственной ЗЛП.
Далее, т.к.
 (3.25)
(3.25)
то, по теореме 3.3 - решение двойственной ЗЛП.
Пусть ИЗ не имеет решения. Предположим противное, что ДЗ имеет решение, тогда по доказанному в первой части теоремы его имеет и ИЗ. Что противоречит условию теоремы.
Следствие 1.
Из выражения (3.23)
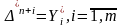 ,
(3.26)
,
(3.26)
следует,
что i-ая
компонента
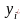 решения
двойственной ЗЛП есть (n+i)-я
симплекс-разность матрицы
,
определяющей оптимальный план исходной
ЗЛП.
решения
двойственной ЗЛП есть (n+i)-я
симплекс-разность матрицы
,
определяющей оптимальный план исходной
ЗЛП.
Следствие 2.
Из выражения (3.21) следует, что j-я симплекс-разность матрицы (j=1,n) равна разности между левой и правой частями ограничений двойственной ЗЛП.
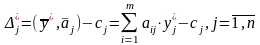 (3.27)
(3.27)
Следствие 3.
Из теорем 3.3 и 3.4 следует, что равенство целевых функций ИЗ и ДЗ является необходимым и достаточным условием оптимальности планов обеих задач.
Теорема 3.5.
Планы
![]() соответственно
прямой и двойственной ЗЛП являются
оптимальными тогда и только тогда, когда
соответственно
прямой и двойственной ЗЛП являются
оптимальными тогда и только тогда, когда
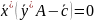 (3.28)
(3.28)
Условия (3.28) называются условиями дополнительной нежесткости.
Необходимость.
Пусть
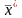 и
и
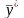 являются
соответственно решениями ИЗ и ДЗ, тогда
являются
соответственно решениями ИЗ и ДЗ, тогда
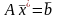 (1)
(1)
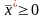 (2)
(2)
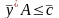 (3)
(3)
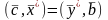 (теорема
3.4) (4)
(теорема
3.4) (4)
Умножая равенство (1) слева на и учитывая (4), получим:
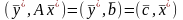 ,
,
откуда
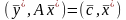 или
.
или
.
Достаточность.
Пусть и являются соответственно планами ИЗ и ДЗ, для которых выполняется условие (3.28).
Для того чтобы доказать оптимальность этих планов, достаточно доказать равенство целевых функций ИЗ и ДЗ (Теорема 3.4, следствие 3).
Имеем:
(1)
(2)
(3)
(4)
Из (4) следует, что
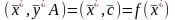 (5)
(5)
Умножая равенство (1) слева на ,получим:
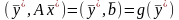 ,
(6)
,
(6)
т.к.
 ,то
с учетом (5) и (6) имеем:
,то
с учетом (5) и (6) имеем:
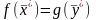 .
.
Примечание
1.
Для основной ЗЛП и двойственной к ней
ЗЛП условия нежесткости имеют вид:
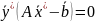
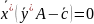 .
(3.29)
.
(3.29)
Примечание 2. Если прямая ЗЛП записана не в канонической форме, то условия дополнительной нежесткости для этой ЗЛП и двойственной к ней ЗЛП могут быть записаны в следующем виде:
если
хj*
>
0, то
 ,
,
если
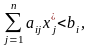 то yi*
=
0, (3.30)
то yi*
=
0, (3.30)
если
yi*
>
0, то
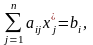
если
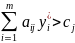 ,
то хj*
= 0.
,
то хj*
= 0.
Теоремы 3.2-3.5 называются основными теоремами двойственности.
Кроме этих теорем можно доказать еще четыре теоремы двойственности.
Теорема 3.6.
Для существования решения одной из пары двойственных задач (и, следовательно, обеих) необходимо и достаточно непустоты множества планов P и Q.
Доказательство.
Необходимость: ИЗ разрешима, следовательно P – непустое множество, следовательно ДЗ разрешима (теорема 3.4), т.е. Q - непустое множество.
Достаточность:
Дано
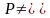 ø
и
ø
и
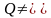 ø,
ø,
Пусть - произвольный план ИЗ, а
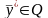 -
фиксированный план ДЗ.
-
фиксированный план ДЗ.
По теореме 3.2:
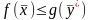
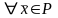 ,
,
следовательно ограничена сверху на ø , т.е по теореме Вейерштрасса ИЗ разрешима.
Пусть - произвольный план ДЗ, а
- фиксированный план ИЗ.
По теореме 3.2:
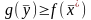
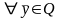
следовательно
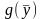 ограничена
снизу на
ø т.е. по теореме Вейерштрасса ДЗ
разрешима.
ограничена
снизу на
ø т.е. по теореме Вейерштрасса ДЗ
разрешима.
Теорема 3.7.
Планы и оптимальны тогда и только тогда, когда
См. следствие 3 из теоремы 3.4.
Теорема 3.8.
Если функция не ограничена сверху ( - снизу) на множестве P(Q), то Q=ø (P=ø).
Доказательство (от противного):
Предположим, что ø ( ø), тогда по теореме 3.6 обе задачи разрешимы, что противоречит условию теоремы.
Теорема 3.9.
Если
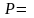 Ø (
Ø (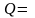 Ø), а
Ø (
Ø),
Ø), а
Ø (
Ø),
то Q – неограниченное множество и не ограничена снизу на нем (P –
неограниченное множество и не ограничена сверху на нем).
Доказательство (от противного): предположим, что Q – ограниченное множество, тогда по теореме Вейерштрасса ДЗ имеет решение, следовательно по теореме 3.4 ИЗ тоже разрешима, а это противоречит условию теоремы, что Ø.
Теорема 3.10.
Рассмотрим задачу оптимального планирования
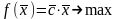
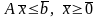
при
данном векторе запасов ресурсов
. Назовем эту задачу
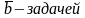 .
Предположим, что при данном конкретном
значении
.
Предположим, что при данном конкретном
значении
 вектора
запасов
все компоненты оптимального плана -
строго положительны. Обозначим
вектора
запасов
все компоненты оптимального плана -
строго положительны. Обозначим
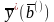
оптимальное
решение задачи, двойственной к
-
задаче. Тогда существует такое
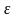 >0,
что если
>0,
что если
 ,
то:
,
то:
ассортимент выпускаемой продукции в оптимальном плане
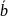 -
задачи
остался прежним (но, вполне возможно,
что количественно изменится);
-
задачи
остался прежним (но, вполне возможно,
что количественно изменится);кроме того, оптимальное решение задачи, двойственной к - задаче осталось неизменным, т.е.
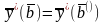 ;
;кроме того, максимальная прибыль в - задаче выражается формулой
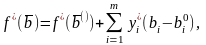 где
где
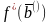 -
максимальная прибыль в
-
максимальная прибыль в
 -
задаче.
-
задаче.
Доказательство этой теоремы довольно сложно и нам не нужно

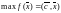 (1)
(1)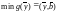 (4)
(4)