2.3.1. Формирование непрерывных случайных величин с заданным законом распределения

Как мы видели, для моделирования методом статистических испытаний необходимо строить искусственный случайный процесс, идентичный в вероятностном смысле реальному случайному процессу. При этом, естественно, законы распределения случайных величин могут быть самыми различными.

Формирование случайной величины с заданным законом распределения вероятностей заключается в генерировании различных значений , которые может принимать случайная величина в исходе -того испытания. Полученная последователь­ность чисел должна быть распределена по заданному закону.

Пусть, например, ведется стрельба по мишени. Случайной ве­тчиной является попадание в одну из зон мишени. Попадания в зоны 8, 6, 3, 1, 7, ... есть возможные значения случайной величины при -том выстреле. Возможны самые различные сово­купности из попаданий, но если условия стрельбы неизменны, то во всех случаях они подчинены одному и тому же закону распределения с математическим ожиданием и дисперсией . Моделирование стрельбы или, что то же, случайной величины заключается в генерировании последовательности случайных чисел, распределенных по такому же закону и с теми же параметрами и , что и попадания при стрельбе.

Закон распределения вероятностей непрерывной величины можно задавать плотностью распределения или интегральной функцией распределения, а дискретной – таблицей распреде­ления вероятностей либо формулой, вы­ражающей вероятность того, что случай­ная величина примет данное значение в функции от самого значения.

Оказывается, случайную величину с требуемым законом распределения веро­ятностей можно получить путем преобра­зования случайной величины , равно­мерно распределенной в интервале

Рис. 2.3. График плотности распределения вероятностей величины

На рисунке 2.3 изображен график плотности распределения вероятностей величины .

На практике величину получают, используя физические генераторы и с помощью специальных программ на ПЭВМ. С помощью программ вычисляют последовательность чисел, которые, хотя и определяются вполне детерминированными отношениями, обладают статистическими свойствами случайных чисел, равномерно распределенных на интервале . Поэтому эти числа называют псевдослучайными.

Имеются специальные таблицы случайных чисел . Они используются главным образом при расчетах по методу статистических испытаний вручную.

Теперь перейдем к рассмотрению методов формирования случайных чисел с заданным законом распределения из случайных чисел .

Одним из основных является метод обратного преобразования или, как его еще называют, метод обратной функции, основанный на использовании свойств интегральной функции распределения.

Пусть требуется сформировать случайную величину , закон распределения которой задан плотностью распределения . Интегральная функция распределения величины

. (2.3.14)

Доказано [10], что значения можно найти из уравнения

. (2.3.15)

Для этого необходимо:

1. вычислить интеграл в левой части уравнения и разрешить полученное выражение относительно ;

2. формировать случайные значения величины и вычислить соответствующие значения .

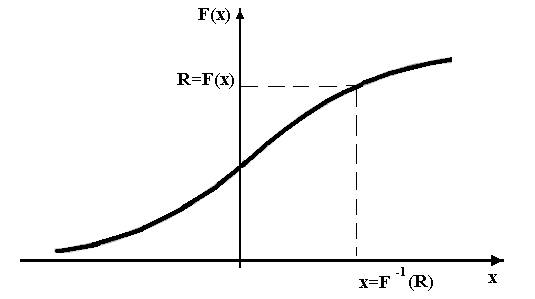
Рис. 2.4. Геометрическая интерпретация метода

При этом каждое значение однозначно определяет реализацию случайной величины с заданной плотностью распределения .

Геометрическая интерпретация метода показана на рис. 2.4. Возьмем на оси ординат случайное значение и примем

. (2.3.16)

Так как монотонная функция, то величина однозначно определяется из выражения (2.3.16):

,

где – обратное отображение величины в область изменения ;

– значение случайной величины , имеющей функцию распределения , или, что то же, плотность рас­пределения .

Рассмотрим примеры формирования случайных величин с по­мощью метода обратного преобразования.

1. Сформировать случайную величину , равномерно распределенную в интервале . В этом случае

.

Вычислим интеграл:

.

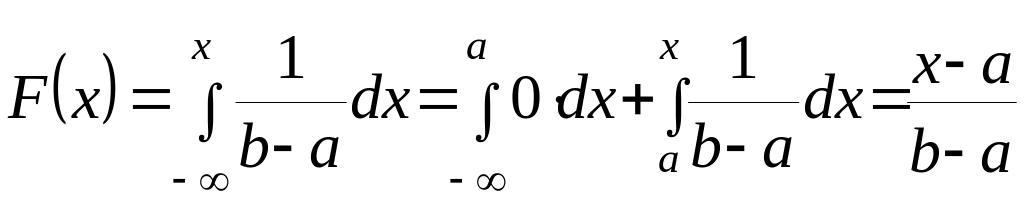Приравняем вычисленный интеграл величине и разрешим полученное выражение относительно , в результате найдем

. (2.3.17)

Теперь будем формировать случайные числа и вычислять соответствующие значения . Каждое из них есть реализация случайной величины , равномерно распределенной в интервале с заданной плотностью .

2. Сформировать случайную величину , распределенную по экспоненциальному (показательному) закону:

.

Получаем

.

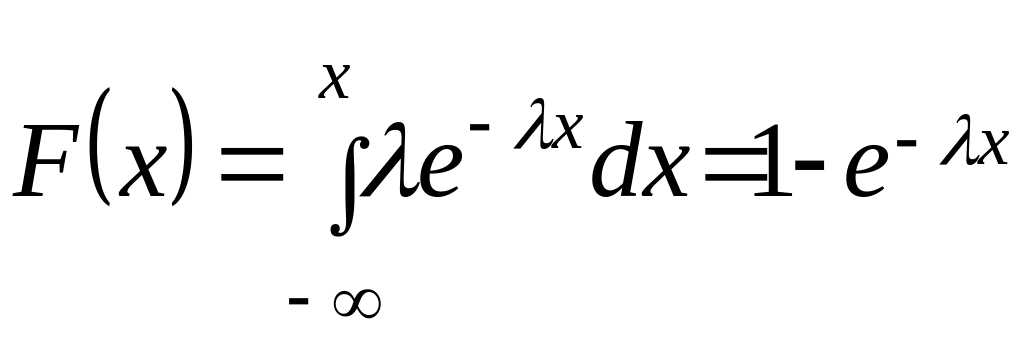Приравняем найденное выражение величине :

.

Логарифмируя, получим

.

Величина распределена по такому же закону, как поэтому можно вместо полученного выражения использовать формулу

. (2.3.18)

Формируя случайные числа и вычисляя соответствующие значения , получим реализацию случайной величины , распределенной по экспоненциальному закону.