
- •Часть 1. Имитационное моделирование. Факторный эксперимент
- •Часть 1. Имитационное моделирование. Факторный эксперимент
- •Предисловие
- •Введение
- •Глава I. Системное моделирование – инструмент управления в больших системах
- •1.1. Понятия системного подхода и большой системы
- •1.2. Эффективность больших систем
- •1.3. Управление в больших системах
- •1.4. Структура систем управления
- •1.5. Основные понятия системного моделирования
- •Глава II. Моделирование систем методом статистических испытаний
- •2.1. Принципы построения математических моделей
- •2.2. Требования, предъявляемые к математическим моделям
- •2.3. Моделирование больших систем методом статистических испытаний. Сущность метода статистических испытаний. Точность метода
- •Вопрос 1.
- •2.3.1. Формирование непрерывных случайных величин с заданным законом распределения
- •2.3.2. Приближенные методы формирования случайных величин с заданным законом распределения вероятностей
- •2.3.3. Моделирование системы массового обслуживания
- •1,07 1,09 1,14 Моделируемое время t
- •2.3.4. Получение наблюдений при моделировании
- •Прикладные задачи имитационного моделирования
- •Ориентированный процесс случайного блуждания как метод прогнозирования
- •2.4.2. Модифицированный имитационным моделированием метод экспоненциального сглаживания
- •Глава III. Оценка качества моделей и планирование статистических испытаний
- •3.1. Оценка качества моделей
- •3.1.1. Методы повышения качества оценок показателей эффективности
- •3.1.2. Пассивные методы повышения качества оценивания показателя эффективности
- •3.1.3. Активные методы повышения качества оценивания показателя эффективности
- •3.1.4. Косвенные методы повышения качества оценивания показателя эффективности
- •3.2. Планирование имитационных экспериментов
- •3.2.1. Общая схема испытаний
- •3.2.2. Полные факторные планы испытаний
- •3.2.3. Дробные факторные планы испытаний. Планирование испытаний
- •3.2.4. Анализ результатов испытаний
- •3.2.5. Оптимальные планы
- •Методы принятия решений по результатам испытаний
- •Общая процедура принятия решений
- •3.3.2. Проверка гипотез о параметрах
- •Принятие решений о стабильности условий испытаний
- •Заключение
- •Библиографический список
- •Предметный указатель
- •Оглавление
- •Глава I. Системное моделирование – инструмент управления в больших системах 6
- •Глава II. Моделирование систем методом статистических испытаний 43
- •Глава III. Оценка качества моделей и планирование статистических испытаний 147
- •191186, Санкт-Петербург, ул. Миллионная, 5
3.3.2. Проверка гипотез о параметрах
Рассмотрим первую группу задач статистической проверки гипотез, обеспечивающих принятие решений о средних значениях параметров. Возможны две основные задачи: проверка соответствия математических ожиданий одноименных параметров (задача проверки однородности), проверка соответствия этих математических ожиданий требованиям ТТЗ (ТУ).
В первом случае
![]() и
и
![]() ,
,
или
![]() ,
,
![]() .
.
Во втором случае
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
С точки зрения
выбора статистики критерия, в первой
задаче исходим из того, что генеральные
средние неизвестны, а во второй –
известны. К числу других признаков
относятся: сведения о
![]() в генеральной совокупности (известно,
неизвестно;
в генеральной совокупности (известно,
неизвестно;
![]() или
или
![]() )
и объеме испытаний (
)
и объеме испытаний (![]() или
или
![]() ;
;
![]() или
или
![]() ).
Заменяя в записи
).
Заменяя в записи
![]() выборочными средними
выборочными средними
![]() ,
приведем наиболее часто используемые
при проверке однородности двух
совокупностей статистики критериев.
,
приведем наиболее часто используемые
при проверке однородности двух
совокупностей статистики критериев.
Если
![]() известно, то применяется статистика
известно, то применяется статистика
 . (3.3.1)
. (3.3.1)
Критическое
значение находится из таблицы Приложения
по величине
.
Гипотеза
принимается, если
![]() .
Формула (3.3.1) применима и в том случае,
если
неизвестно, но обе
спечена равная
точность измерений
.
Формула (3.3.1) применима и в том случае,
если
неизвестно, но обе
спечена равная
точность измерений
![]() и
и
![]() .
При малом числе испытаний
.
При малом числе испытаний
![]() и неизвестном значении
используется статистика
-критерия:
и неизвестном значении
используется статистика
-критерия:
 ,
,
 .
(1.3.2)
.
(1.3.2)
Когда
![]() ,
,
![]() ,
,
![]() ,
применяется статистика
,
применяется статистика
 . (3.3.3)
. (3.3.3)
При меньшем числе испытаний и используется статистика
 ,
,
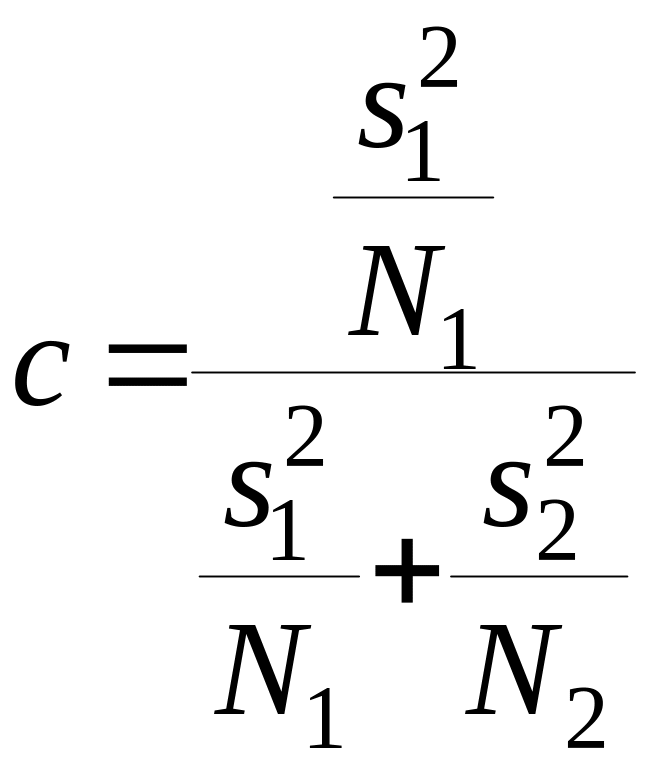 .
(3.3.4)
.
(3.3.4)
Число степеней
свободы определяется из условия
 .
Этот вариант соответствует случаю,
когда испытания проводятся в различных
условиях или различными приборами
(методами).
.
Этот вариант соответствует случаю,
когда испытания проводятся в различных
условиях или различными приборами
(методами).
Из приведенных зависимостей видно, что для проверки гипотез о средних необходимо предварительно проверить стабильность условий испытаний (гипотезы о дисперсиях).
При проверке
гипотез
![]() ,
если значение
,
если значение
![]() известно, вместо формулы (3.3.1) применяется
известно, вместо формулы (3.3.1) применяется
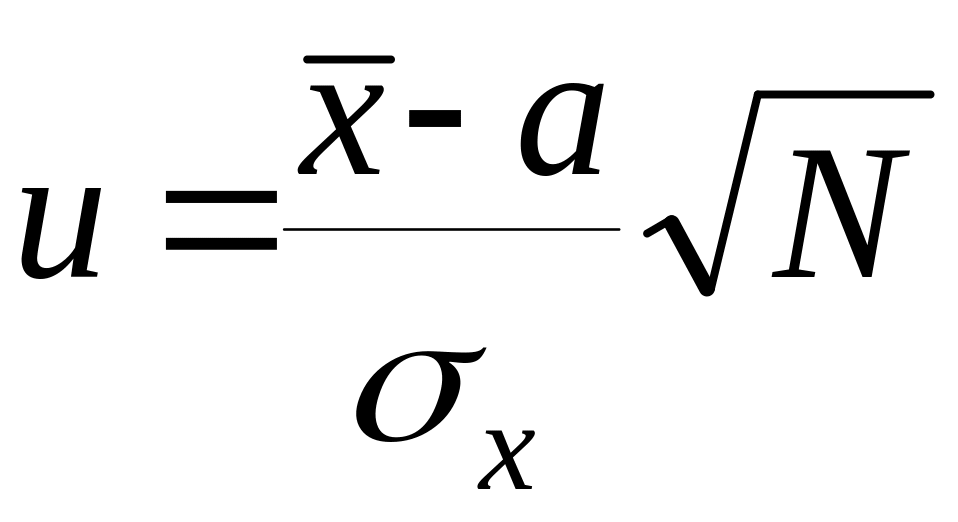 ,
,
а если сведения о отсутствуют, то
 ,
,
![]() . (3.3.5)
. (3.3.5)
Принятие решений о стабильности условий испытаний
Принятие решений о характеристиках точности осуществляется по результатам проверки гипотез относительно дисперсий (или
среднего
квадратического отклонения): 1)
![]() ,
,
![]() или
или
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() или
или
![]() ,
,
![]() .
Для второго случая характерна задача
проверки стабильности условий испытаний,
когда сравнивается точность работы
приборов, инструмента или используемых
методов измерений. Для проверки гипотезы
применяется статистика
-распределения
.
Для второго случая характерна задача
проверки стабильности условий испытаний,
когда сравнивается точность работы
приборов, инструмента или используемых
методов измерений. Для проверки гипотезы
применяется статистика
-распределения
 (3.3.6)
(3.3.6)
или статистика
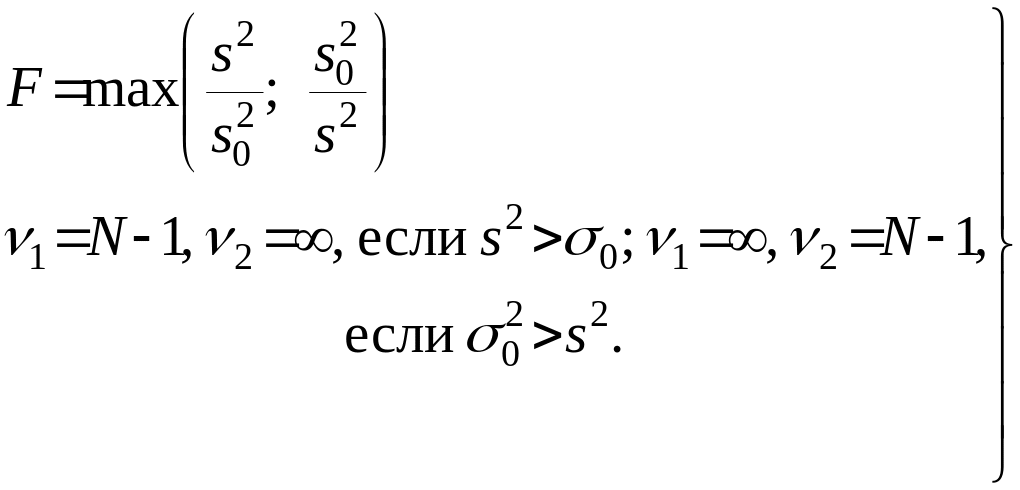 (3.3.7)
(3.3.7)
Критическое значение выбирается по табл. П.2.6 по , и .
Пример.
По данным летных испытаний (
)
получена оценка среднего квадратического
отклонения по дальности
![]() км. Проверить при
км. Проверить при
![]() соответствие установленному в ТЗ
требованию
соответствие установленному в ТЗ
требованию
![]() км.
км.
Решение.
Выдвигается гипотеза
 ,
,
 .
.Для проверки гипотезы выбирается -критерий.
По ,
 (так как
(так как
 ),
),
 из
табл. П.2.6 получаем
из
табл. П.2.6 получаем
 .
.
Статистическое решение: гипотеза не противоречит результатам испытания и может быть принята. Инженерное решение: рассеивание по дальности удовлетворяет требованиям ТЗ.
Если сравнивается
несколько дисперсий (![]() ),
то используют критерий Кохрена (если
число испытаний
),
то используют критерий Кохрена (если
число испытаний
![]() )
или критерий Бартлетта.
)
или критерий Бартлетта.
Статистика критерия Кохрена
 ;
;
 .
(3.3.8)
.
(3.3.8)
Критическое
значение
![]() определяется по табл. П.2----?.
определяется по табл. П.2----?.
Статистика критерия Бартлетта
 ,
,
![]() . (3.3.9)
. (3.3.9)
где
 ;
;
 ;
;
 ,
подчиняется
,
подчиняется
![]() -распределению
с
-распределению
с
![]() степенями свободы. Значение
степенями свободы. Значение
![]() находится по табл. П.2.4-----?.
находится по табл. П.2.4-----?.
Обозначим через
исследуемую случайную величину.
Пусть требуется проверить гипотезу
о том, что эта случайная величина
подчиняется закону распределения
.
Для проверки гипотезы произведем
выборку, состоящую из
независимых наблюдений над случайной
величиной
.
По выборке можно построить эмпирическое
распределение
![]() исследуемой случайной величины.
Сравнение эмпирического
и теоретического распределений
производится с помощью, специально
подобранной случайной величины –
критерия согласия. Существует несколько
критериев согласия:
Пирсона, Колмогорова, Смирнова и др.
исследуемой случайной величины.
Сравнение эмпирического
и теоретического распределений
производится с помощью, специально
подобранной случайной величины –
критерия согласия. Существует несколько
критериев согласия:
Пирсона, Колмогорова, Смирнова и др.
Критерий согласия Пирсона – наиболее часто употребляемый критерий для проверки гипотезы о законе распределения.
Рассмотрим этот
критерий. Разобьем всю область изменения
на
интервалов
![]() и подсчитаем количество элементов
,
попавших в каждый из интервалов
и подсчитаем количество элементов
,
попавших в каждый из интервалов
![]() .
Предполагая известным теоретический
закон распределения
,
всегда можно определить
.
Предполагая известным теоретический
закон распределения
,
всегда можно определить
![]() (вероятность попадания случайной
величины
в интервал
),
тогда теоретическое число значений
случайной величины
,
попавших в интервал
,
можно рассчитать по формуле
(вероятность попадания случайной
величины
в интервал
),
тогда теоретическое число значений
случайной величины
,
попавших в интервал
,
можно рассчитать по формуле
![]() .
Результаты проведенных расчетов
объединим в табл. 3.2.
.
Результаты проведенных расчетов
объединим в табл. 3.2.
Таблица 3.2
Интервалы |
|
|
… |
|
… |
|
Эмпирические
частоты
|
|
|
… |
|
… |
|
Теоретические частоты |
|
|
… |
|
… |
|
Здесь
![]() ;
;
![]() .
.
Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезу следует отвергнуть, в противоположном случае – принять.
Сформулируем критерий, который бы характеризовал степень расхождения между эмпирическими и теоретическими частотами. В литературе по математической статистике доказывается, что статистика

имеет распределение
с
![]() степенями свободы. Здесь
число параметров распределения
степенями свободы. Здесь
число параметров распределения
![]() ,
рассчитанных по выборке.
,
рассчитанных по выборке.
Правило применения
критерия
сводится к следующему. Рассчитав значение
и выбрав уровень значимости критерия
,
по таблице
-распределёния
определяют
![]() .
Если
.
Если
![]() ,
то гипотезу
отвергают, если
,
то гипотезу
отвергают, если
![]() ,
то гипотезу принимают. Очевидно, что
при проверке гипотезы о законе
распределения контролируется лишь
ошибка первого рода.
,
то гипотезу принимают. Очевидно, что
при проверке гипотезы о законе
распределения контролируется лишь
ошибка первого рода.
В заключение заметим, что необходимым условием применения критерия Пирсона является наличие в каждом из интервалов по меньшей мере 5-10 наблюдений. Если количество наблюдений в отдельных интервалах очень мало (порядка 1-2), то имеет смысл объединить некоторые интервалы. Проиллюстрируем применение критерия на двух примерах. В примере 6.5 разберем случай, когда ставится гипотеза о том, что исследуемая случайная величина подчиняется закону Пуассона, а в примере 6.6 – нормальному закону распределения.
Пример 6.5.
На телефонной станции производились
наблюдения за числом
неправильных соединений в минуту.
Наблюдения в течение часа дали следующие
результаты: 3; 1; 3; 1; 4; 2; 2; 4; 0; 3; 0; 2; 2; 0; 2; 1;
4; 3; 3;; 1; 4; 2; 2; 1; 1; 2; 1; 0; 3; 4; 1; 3; 2; 7; 2; 0; 0; 1; 3;
3; 1; 2; 4; 2; 0; 2; 3; 1; 2; 5; 1; 1; 0; 1; 1; 2; 2; 1; 1; 5.
Определить среднюю арифметическую и
дисперсию неправильных соединений в
минуту и проверить выполнение основного
условия для распределения Пуассона
![]() .
Найти теоретическое распределение
Пуассона и проверить степень согласия
теоретического и эмпирического
распределений по критерию
Пирсона при уровне значимости
.
Найти теоретическое распределение
Пуассона и проверить степень согласия
теоретического и эмпирического
распределений по критерию
Пирсона при уровне значимости
![]() .
.
Решение. Упорядочим результаты наблюдений, записав их в следующую таблицу
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
17 |
16 |
10 |
6 |
2 |
0 |
1 |
Обозначим через
![]() среднее число неправильных соединении
в минуту. Имеем
среднее число неправильных соединении
в минуту. Имеем
![]()
Вычислим выборочную оценку дисперсии:
![]()
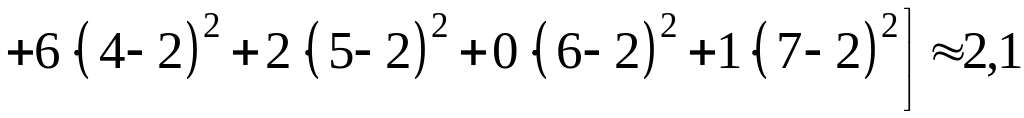
Необходимое условие
для распределения Пуассона
![]() практически выполняется. Запишем
теоретический закон Пуассона; в виде
практически выполняется. Запишем
теоретический закон Пуассона; в виде
 .
.
Так как значение математического ожидания неизвестно, то подставим вместо него оценку по выборке. Имеем:
 3,
3,
 ,
,
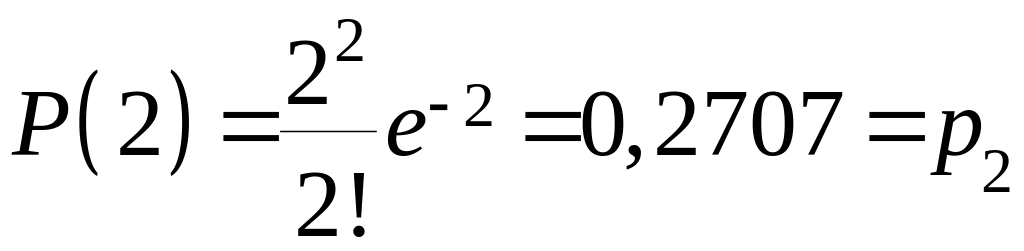 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Запишем полученные результаты в таблицу 3.3.
Таблица 3.3
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
17 |
16 |
10 |
6 |
2 |
0 |
1 |
|
8,1 |
16,24 |
16,24 |
10,62 |
5,41 |
2,166 |
0,72 |
0,204 |
Объединим столбцы 5, 6 и 7, так как в каждом из них мало наблюдений. Тогда таблица преобразуется (табл. 3.4).
Таблица 3.4
|
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
1 |
2 |
3 |
4 |
5 и более |
|
8 |
17 |
16 |
10 |
6 |
3 |
|
8,1 |
16,24 |
16,24 |
10,82 |
5,41 |
3,09 |
Вычислим значение :
![]()
![]() .
.
Примем уровень
значимости
.
Количество интервалов
![]() .
По выборке вычислен, один параметр,
которым определяется закон Пуассона
– математическое ожидание; следовательно,
.
По выборке вычислен, один параметр,
которым определяется закон Пуассона
– математическое ожидание; следовательно,
![]() .
Поэтому число степеней свободы
.
Поэтому число степеней свободы
![]() .
В табл. 7---------?
приложений значениям
и
.
В табл. 7---------?
приложений значениям
и
![]() соответствует
соответствует
![]() .
Имеем
.
Имеем
![]() ,
следовательно, нет оснований отвергнуть
проверяемую гипотезу.
,
следовательно, нет оснований отвергнуть
проверяемую гипотезу.
Таблица 3.5
№ интервала |
|
|
1 |
40-41 |
20 |
2 |
41-42 |
112 |
3 |
42-43 |
154 |
4 |
43-44 |
73 |
5 |
44-45 |
13 |
6 |
45-46 |
2 |
|
|
374 |
Решение. Как следует из анализа интервального вариационного ряда, необходимо объединить интервалы 5 и 6, так как в интервале 6 количество наблюдений менее 5. В результате объединения получим следующий ряд распределения:
|
40-41 |
41-42 |
42-43 |
43-44 |
44-46 |
|
20 |
112 |
154 |
73 |
15 |
Т еперь
найдем вероятность
еперь
найдем вероятность
![]() ;
;
![]() выражает вероятность того, что
случайная величина
,
имеющая нормальный закон распределения,
принимает значение, принадлежащее
интервалу (40; 41), то есть
выражает вероятность того, что
случайная величина
,
имеющая нормальный закон распределения,
принимает значение, принадлежащее
интервалу (40; 41), то есть


![]()
Аналогично получаем:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Для нахождения статистики удобно составить таблицу (табл. 3.6).
Таблица 3.6
№ п/п |
|
|
|
|
|
|
|
1 |
40-41 |
20 |
0,0660 |
24,76 |
4,76 |
21,56 |
0,871 |
2 |
41-42 |
112 |
0,2762 |
103,70 |
8,30 |
68,89 |
0,664 |
3 |
42-43 |
154 |
0,3971 |
148,52 |
5,48 |
29,03 |
0,127 |
4 |
43-44 |
73 |
0,2128 |
79,59 |
6,59 |
43,43 |
0,546 |
5 |
44-46 |
15 |
0,0417 |
15,60 |
0,60 |
0,36 |
0,023 |
|
|
374 |
0,9938 |
372,17 |
|
|
2,231= |
Количество
интервалов
![]() .
По выборке рассчитаны два параметра:
оценки для математического ожидания и
дисперсии, следовательно,
.
По выборке рассчитаны два параметра:
оценки для математического ожидания и
дисперсии, следовательно,
![]() .
Число
степеней свободы
.
Число
степеней свободы
![]() .
.
В
табл. 7-----------?
приложений
![]() и
соответствует
и
соответствует
![]() .
Имеем
.
Имеем
![]() ,
следовательно, нет оснований отвергнуть
гипотезу
о нормальности распределения предела
текучести.
,
следовательно, нет оснований отвергнуть
гипотезу
о нормальности распределения предела
текучести.

