2.3.2. Приближенные методы формирования случайных величин с заданным законом распределения вероятностей

При решении многих задач плотность распределения вероятностей задается графически либо она задана аналитически, но интеграл (2.3.14) не выражается через элементарные функции. Например, плотность нормального распределения случайной величины имеет вид

(2.3.19)

и интеграл (2.3.14) не берется. В этих случаях метод обратного образования использовать нельзя и применяются приближенные методы формирования случайных величин.

В настоящем параграфе рассматривается один достаточно универсальный метод, применяемый для формирования случайных величин:

• по любому дискретному распределению;

• по любому непрерывному распределению, которое можно аппроксимировать дискретным;

• по любому эмпирическому распределению.

Метод допускает весьма простую реализацию на ПЭВМ и во многих случаях обеспечивает необходимую точность преобразования. Поэтому он широко распространен на практике.

Изложение метода начнем с рассмотрения способа формирования дискретной случайной величины с заданным законом распределения вероятностей.

Пусть требуется сформировать значения дискретной случайной величины , закон распределения которой задан таблицей

, .

Разобьем интервал от до на интервалов, длины которых равны , а сами интервалы пронумеруем числами соответственно (рис. 2.5). Координаты точек деления:

Будем формировать случайные числа , равномерно распреде­ленные в интервале . Вероятность того, что число попадет в некоторый интервал внутри интервала , равна длине этого интервала (см. рис. 2.3). Действительно, какой бы ин­тервал внутри мы ни взяли, вероятность того, что окажется внутри , равна

,

то есть длине интервала .

1 2 … …

0 p₁ y₁ p₂ y₂ y_i-1 p_i y_i y_n-1 p_n 1

Рис. 2.5. Формирование случайных чисел на интервале

Следовательно, вероятность того, что случайное число попа­дет в первый интервал, равна

,

в -тый интервал

. (2.3.20)

Таким образом, если сформированное случайное число попа­дет в интервал с номером , то можно считать, что в данном опыте случайная величина принимает значение .

Описанный способ формирования дискретных случайных вели­чин легко реализуется на ПЭВМ. Покажем это на примере. Пусть – дискретная случайная величина, закон распределения которой задан таблицей

.

В памяти ПЭВМ в ста последовательно пронумерованных ячей­ках записывается: в первые 16 ячеек – величина , в следующие 31 ячейку –величина , в следующие 22 ячейки – величина и т. д. Формируется случайное двузначное десятичное число и умножается на , так что . На­пример, если , принимают , так как в два­дцать девятой ячейке записано значение . Этот процесс по­вторяется столько раз, сколько требуется.

Теперь перейдем к изложению приближенного метода формирования случайных величин.

Пусть требуется получить случайную величину , закон распределения которой задан графиком плотности распределения . Область изменения возможных значений величины ограничена в пределах . Если область определения ограничена, нужно перейти к ограниченной области. Например, для нормального распределения можно принять .

Рис. 2.6. График плотности распределения

Разобьем область на равных между собой интервалов (рис.2.6,а) и вычислим площади , элементарных криволинейных трапеций, ограниченных кривой , ординатами и отрезком абсциссы . Площадь можно вычислить по формуле трапеций

.

Построим далее на каждом интервале прямоугольник, площадь которого равна площади соответствующей элементарной криволинейной трапеции. Высота -того прямоугольника

.

Так как мы приняли, что все возможные значения случайной величины сосредоточены в конечном интервале , то функ­ция должна быть нормирована условием

. (2.3.21)

Геометрически этот интеграл выражается площадью криволи­нейной трапеции , ограниченной кривой и осью абсцисс. Что­бы выполнить условие (2.3.21), нужно площади , вычисленные в каких-то единицах, разделить на площадь , вычисленную в тех же единицах.

Тогда площадь каждой элементарной криволинейной трапеции будет выражена в безразмерных единицах, а их сумма равна единице

,

где – нормированная площадь элементарной криволинейной трапеции.

Очевидно, что вероятность попадания значения в интервал равна площади :

. (2.3.22)

Ступенчатая линия, образованная сторонами прямоугольников, параллельными оси абсцисс, аппроксимирует кривую распределе­ния вероятностей .

Для получения возможных значений случайной величины необходимо:

1. произвести случайный выбор интервала из возможных ин­тервалов (пусть это будет -тый интервал);

2. произвести случайный выбор числа на -том интервале.

Первый шаг осуществляется следующим образом. Разобьем, как это было сделано при формировании дискретной случайной величины, интервал от до на интервалов, длины которых равны (рис. 2.6, 6). Координаты точек деления:

. Сформируем случайное число . Согласно формуле (2.3.20) вероятность попадания числа в -тый интервал равно :

. (2.3.23)

С другой стороны, в соответствии с формулой (2.3.22) вероятность попадания случайной величины в интервал также равна .

. (2.3.24)

Поэтому, если сформированное случайное число окажется интервале , то согласно выражениям (2.3.23) и (2.3.24) случайная величина принадлежит интервалу .

Перейдем ко второму шагу. На каждом интервале кривая распределения вероятностной аппроксимирована отрезком ступенчатой линии, параллельным оси абсцисс. Это означает, что в интервале случайная величина имеет равномерное распределение. Поэтому случайное число можно получить следующим образом: сформировать второе случайное число по формуле (2.3.17), положив в ней , вычислить

. (2.3.25)

Многократно повторяя описанную процедуру, получим последовательность случайных чисел с графиком плотности распределения в виде ступенчатой линии, приближенно представляющей кривую распределения . Приближение будет тем точнее, чем на большее число интервалов разбита область определения функции и чем точнее вычислены нормированные площади элементарных криволинейных трапеций.

Таким образом, для реализации изложенного метода на ПЭВМ необходимо:

1. Разбить область определения функции на интервалов и вычислить значения . Обозначим через количество десятичных знаков в числе .

2. В последовательно пронумерованных ячейках памяти ПЭВМ хранить границы интервалов: в первых ячейках – границы первого интервала, в следующих ячейках – границы второго интервала и т.д.

3. Сформировать случайное число с десятичными знаками, умноженное на , и проверкой системы неравенств

найти номер интервала, которому принадлежит .

4. По формулам

;

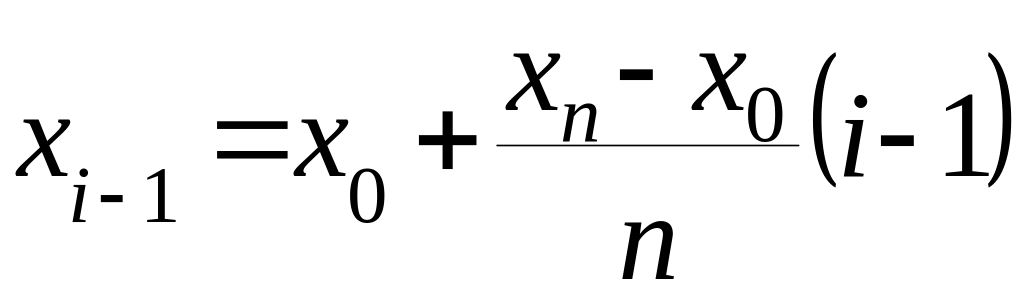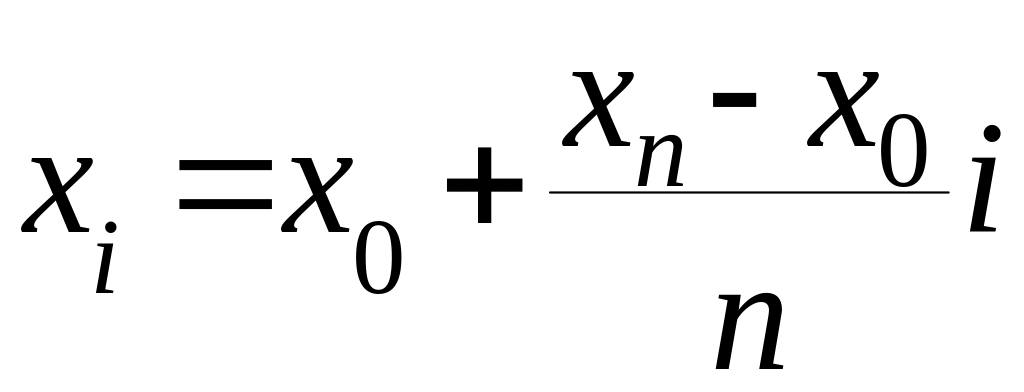
вычислить границы интервала, которому принадлежит .

Сформировать второе случайное число и по формуле (2.3.25) вычислить значение .

Метод весьма эффективен с точки зрения количества команд на формирование одного случайного числа .