Некоррелированность и статистическая независимость

Если совместно рассматривать две случайные величины Х₁ и Х₂, между ними мо­жет существовать либо не существовать статистическая, связь. Отсутствие та­кой связи означает, что плотность вероятности одной случайной величины не за­висит от того, какое значение принимает другая случайная величина. Двумерная плотность вероятности при этом представляет собой произведение одномерных плотностей:

p(x₁, x₂) = p₁(x₁)p₂(x₂).

Это условие называется условием статистической независимости.

При наличии статистической связи между случайными величинами статистиче­ские свойства каждой из них зависят от значения, принимаемого другой случай­ной величиной. Эта связь может быть сильной или слабой, линейной или нели­нейной. Мерой линейной статистической связи между случайными величинами является коэффициент корреляции:

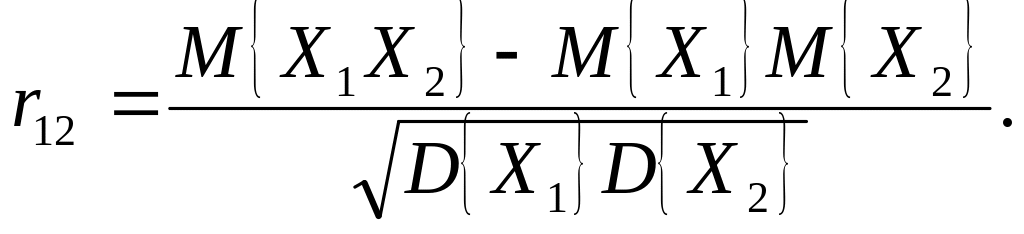(1.42)

Можно показать, что . Предельные значения ±1 достигаются, если реали­зации случайных величин жестко связаны линейным соотношением x₂ = ax₁+b ,где а и b — некоторые константы. Знак коэффициента корреляции при этом сов­падает со знаком множителя а.

Равенство коэффициента корреляции нулю свидетельствует об отсутствии ли­нейной статистической связи между случайными величинами (при этом говорят об их некоррелированности). Как видно из (1.42), при этом математическое ожи­дание произведения случайных величин равно произведению их математиче­ских ожиданий:

Легко показать, что из статистической независимости следует некоррелирован­ность случайных величин. Обратное утверждение в общем случае неверно — не­коррелированные случайные величины могут быть зависимыми.

ЗАМЕЧАНИЕ

Классическим примером этого является пара случайных величин x₁ = cos φ и x₂ = sin φ, где φ — случайная величина, равномерно распределенная на интервале 0 ...2π. Очевидно, что x₁ и x₂ зависят друг от друга; однако их коэффициент корреляции оказывается равным нулю.

Стационарные и эргодические случайные процессы

В общем случае, как уже говорилось, вероятностные и корреляционные характе­ристики случайных процессов зависят от одного или нескольких моментов вре­мени, в которые эти характеристики определяются. Однако существует класс случайных процессов, у которых зависимость характеристик от времени отсутст­вует. Кроме того, для некоторых случайных процессов не обязательно произво­дить усреднение по ансамблю реализаций — можно ограничиться рассмотрением одной реализации и ее усреднением во времени.

Такие случайные процессы будут рассматриваться в данном разделе.

Стационарные случайные процессы

Так принято называть случайные процессы, статистические характеристики ко­торых одинаковы во всех временных сечениях.

Говорят, что случайный процесс строго стационарен (или стационарен в узком смысле), если его многомерная плотность вероятности p(x₁, x₂, …, x_n, t₁, t₂, …, t_n) произвольной размерности п не изменяется при одновременном сдвиге всех вре­менных сечений t₁, t₂, …, t_n вдоль оси времени на одинаковую величину τ:

p(x₁, x₂, …, x_n, t₁, t₂, …, t_n)= p(x₁, x₂, …, x_n, t₁+τ, t₂+τ, …, t_n+τ) при любом τ.

Если же ограничить требования тем, чтобы от временного сдвига не зависели лишь одномерная и двумерная плотности вероятности, то такой случайный про­цесс будет стационарен в широком смысле. Понятно, что из стационарности в уз­ком смысле следует стационарность в широком смысле, но не наоборот.

Для стационарного случайного процесса математическое ожидание и дисперсия не зависят от времени, а корреляционная функция зависит не от самих моментов времени, а только от интервала между ними τ = t₂ – t₁:

R_x(t₁, t₂) = R_x(t₂-t₁) = R_x(τ).

По этой причине при записи статистических параметров стационарного случай­ного процесса можно опускать обозначения фиксированных моментов времени:

m_x, D_x, K_x(τ), R_x(τ).

Легко убедиться, что корреляционная функция стационарного случайного про­цесса является четной:

R_x(-τ) = R_x(τ).

Кроме того, абсолютные значения этой функции при любых τ не превышают ее значения при τ = 0 (напомним, что это значение равно дисперсии случайного процесса):

Часто удобно использовать коэффициент корреляции (его также называют нор­мированной корреляционной функцией)

Для коэффициента корреляции выполняются соотношения и

Функции и характеризуют связь (корреляцию) между значения­ми X(t) разделенными промежутком τ. Чем медленнее убывают эти функции с ростом абсолютного значения τ, тем больше промежуток, в течение которого на­блюдается статистическая связь между мгновенными значениями случайного процесса, и тем медленнее, плавнее изменяются во времени его реализации.

Легко видеть, что гармонический процесс со случайной начальной фазой (см, раздел «Модели случайных процессов» и вычисление характеристик этого процесса в разделе «Корреляционные функции случайных процессов») является стационарным в широком смысле. Действительно, зависящие от одно­мерной плотности вероятности математическое ожидание (1.39) и дисперсия (1.41) не зависят от времени, а корреляционная функция (1.40), зависящая от двумерной плотности вероятности, зависит лишь от интервала между рассмат­риваемыми моментами времени:

(1.43)

Коэффициент корреляции такого случайного процесса равен

ЗАМЕЧАНИЕ

Здесь следует отметить, что стационарным будет любой случайный процесс, реализации которого являются периодическими функциями, идентичными по форме и различающи­мися лишь «начальной фазой», то есть положением начала отсчета времени в пределах пе­риода. При этом принципиальной является равномерность распределения начальной фразы в пределах периода. Действительно, пусть у гармонического процесса начальная фаза равномерно распределена в пределах половины окружности — на интервале 0...π. Ма­тематическое ожидание процесса в этом случае будет равно

Результат вычислений показывает, что математическое ожидание процесса зависит oт времени, следовательно, он не является стационарным.