Комплексная форма

Данная форма представления ряда Фурье является, пожалуй, наиболее употре­бимой в радиотехнике. Она получается из вещественной формы представлением косинуса в виде полусуммы комплексных экспонент (такое представление выте­кает из формулы Эйлера e^jx = cos x + j sin x):

cos x = ½ (e^jx + e^-jx).

Применив данное преобразование к вещественной форме ряда Фурье, получим суммы комплексных экспонент с положительными и отрицательными показате­лями:

А теперь будем трактовать экспоненты со знаком «минус» в показателе как чле­ны ряда с отрицательными номерами. В рамках этого же общего подхода посто­янное слагаемое а₀/2 станет членом ряда с нулевым номером. В результате полу­чится комплексная форма записи ряда Фурье:

. (1.8)

Комплексные коэффициенты ряда связаны с амплитудами А_к и фазами φ_k фигу­рирующими в вещественной форме записи ряда Фурье (1.7), следующими не­сложными соотношениями:

,

, .

Несложно выглядят и формулы связи с коэффициентами а_к и b_k синусно-косинусной формы ряда Фурье (1.6):

,

, .

Отсюда сразу же следует и формула непосредственного расчета коэффициентов С_к ряда Фурье в комплексной форме:

. (1.9)

Если s(t) является четной функцией, коэффициенты ряда С_к будут чисто веще­ственными-, а если s(t) — функция нечетная, коэффициенты ряда окажутся чис­то мнимыми.

Совокупность амплитуд гармоник ряда Фурье часто называют амплитудным спектром, а совокупность их фаз — фазовым спектром. Эти понятия не следует путать с амплитудно- и фазочастотными характеристиками, которые относятся не к сигналам, а к цепям.

Если анализируемый сигнал s(t) является вещественным, то его амплитудный и фазовый спектры обладают симметрией:

, , .

Раздел 2. Преобразование Фурье. Примеры разложения сигналов в ряд Фурье

В данном разделе мы применим ряд Фурье для анализа конкретных сигналов.

Последовательность прямоугольных импульсов

Первым рассматриваемым сигналом будет последовательность прямоугольных импульсов с амплитудой A, длительностью τ и периодом повторения Т. Начало отсчета времени примем расположенным в середине импульса (рис. 1.3).

Рис. 1.3. Периодическая последовательность прямоугольных импульсов

Данный сигнал является четной функцией, поэтому для его представления удоб­нее использовать синусно-косинусную форму ряда Фурье — в ней будут присут­ствовать только косинусные слагаемые а_k равные

.

Внимательно рассматривая полученную формулу, можно заметить, что длитель­ность импульсов и период их следования входят в нее не обособленно, а исклю­чительно в виде отношения. Этот параметр — отношение периода к длитель­ности импульсов — называют скважностью последовательности импульсов и обозначают буквой q: q = T/τ. Введем этот параметр в полученную формулу для коэффициентов ряда Фурье, а затем приведем формулу к виду sin(x)/x:

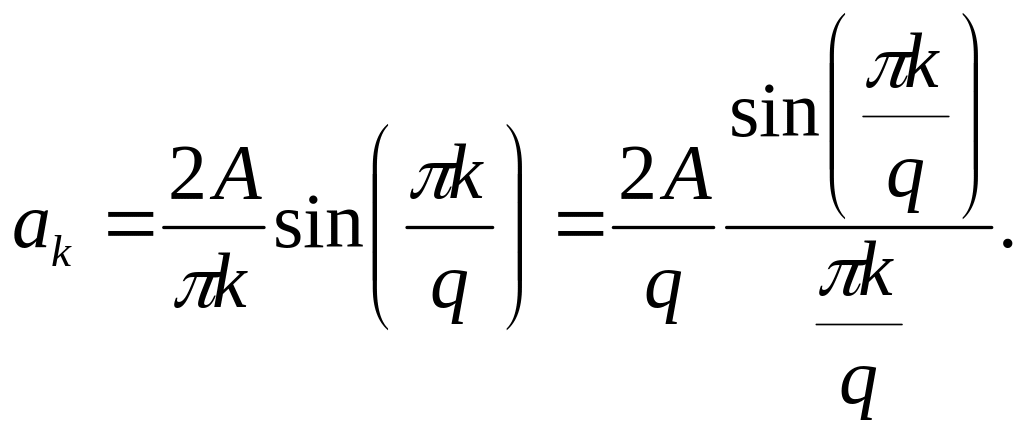(1.10)

ЗАМЕЧАНИЕ

В зарубежной литературе вместо скважности используется обратная величина, называе­мая коэффициентом заполнения (duty cycle) и равная τ/Т.

При такой форме записи становится хорошо видно, чему равно значение посто­янного слагаемого ряда: поскольку при х → 0 sin(x)/x → 1, то

.

Теперь можно записать и само представление последовательности прямоуголь­ных импульсов в виде ряда Фурье:

.

Амплитуды гармонических слагаемых ряда зависят от номера гармоники по за­кону sin(х)/х (рис. 1.4).

График функции sin(x)/x имеет лепестковый характер. Говоря о ширине этих лепестков, следует подчеркнуть, что для графиков дискретных спектров перио­дических сигналов возможны два варианта градуировки горизонтальной оси — в номерах гармоник и в частотах. На рис. 1.4 градуировка оси соответствует но­мерам гармоник, а частотные параметры спектра нанесены на график с помощью р аз мерных линий.

Итак, ширина лепестков, измеренная в количестве гармоник, равна скважности последовательности (при имеем ) = 0, если ). Отсюда следу­ет важное свойство спектра последовательности прямоугольных импульсов — в нем отсутствуют (имеют нулевые амплитуды) гармоники с номерами, кратны­ми скважности.

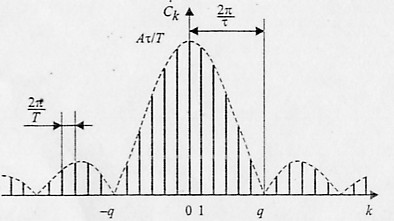
Рис. 1.4. Коэффициенты ряда Фурье для последовательности прямоугольных импульсов

Расстояние по частоте между соседними гармониками равно частоте следования импульсов — 2π/Т. Ширина лепестков спектра, измеренная в единицах частоты, равна 2π/τ, то есть обратно пропорциональна длительности импульсов. Это, как мы увидим далее, проявление общего закона — чем короче сигнал, тем шире его спектр.

Меандр

Важным частным случаем предыдущего сигнала является меандр — последова­тельность прямоугольных импульсов со скважностью, равной двум, когда дли­тельности импульсов и промежутков между ними становятся равными (рис. 1.5).

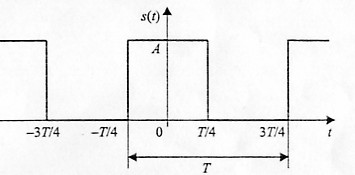
Рис. 1.5. Меандр

Подставив q = 2 в формулу (1.10), получим

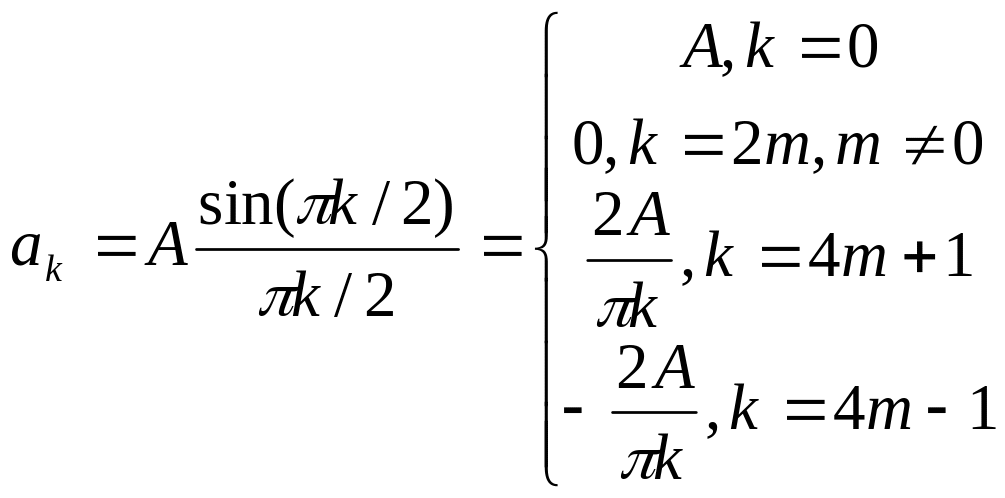
Здесь m – произвольное целое число.

Таким образом, в спектре меандра присутствуют только нечетные гармоники. Это согласуется с общим правилом, приведенным выше. Представление меандра в виде ряда Фурье с учетом этого может быть записано следующим образом:

.

Гармонические составляющие, из которых складывается меандр, имеют ампли­туды, обратно пропорциональные номерам гармоник, и чередующиеся знаки.

Покажем на примере меандра; как складывается заданный сигнал из отдельных гармоник (рис. 1.6):

« N=8 % число ненулевых гармоник

« t+-1:0.01:1: % вектор моментов времени

« A=1 % амплитуда

« T=1 % период

« nh=(1:N)*2-1; % номера ненулевых гармоник

« % строки - гармоники

« harmonics=cos(2*pi*nh’*t\T):

« Am=2/pi./nh % амплитуды гармоник

« Am=(2:2:end)=-Am(2:2:end) % чередование знаков

« s1= harmonics .*repmat(Am’. 1. length(t))

« % строки – частичные суммы гармоник

« s2=cumsum(s1):

« for k=1:N. subplot(4. 2. k). plot(t. s2(k.:)). end

Вообще, последовательность прямоугольных импульсов плохо подходит для пред­ставления рядом. Фурье — она содержит скачки, а сумма любого числа гармони­ческих составляющих с любыми амплитудами всегда будет непрерывной функ­цией. Поэтому поведение ряда Фурье в окрестностях разрывов представляет особый интерес. На графиках рис. 1.6 хорошо видно, что в окрестности точки разрыва суммирование ряда Фурье дает наклонный участок, причем; крутизна наклона возрастает с ростом числа суммируемых гармоник. В самой точке раз­рыва ряд Фурье сходится к полусумме правого и левого пределов:

.

Здесь s(t)....... исходный сигнал, s'(t) — сумма ряда Фурье для него.

Рис. 1.6. Промежуточные стадии суммирования ряда Фурье для меандра

На примыкающих к разрыву участках сумма ряда Фурье дает заметные пульса­ции, причем на графиках рис. 1.6 заметно, что амплитуда этих пульсаций не уменьшается с ростом числа суммируемых гармоник — пульсации лишь сжима­ются по горизонтали, приближаясь к точке разрыва. Это явление, присущее ря­дам Фурье для любых сигналов с разрывами первого рода (скачками), называет­ся эффектом Гиббса. Можно показать, что амплитуда первого (самого большого) выброса составляет примерно 9 % от величины скачка.