8)Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа.

теорема Пуассона

Если вероятность р наступления события А в каждом испытании стремится к нулю (р → 0) при неограниченном увеличении числа n испытаний (n → ∞), причем произведение np стремится к постоянному числу λ (np → λ), то вероятность Рm,n того, что со-бытие А появится m раз в n независимых испытаниях, удовлетворяет предельному равенству:

формула Пуассона для маловероятных событий:

Если вероятность р — постоянна и мала, число испытаний n — велико и число λ = nр — незначительно (будем полагать, что λ = nр < 10), то из предельного равенства вытекает приближенная формула Пуассона:

Локальная теорема Муавра – Лапласа.

Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Рmn того, что событие А произойдет m раз в n независимых испытаниях при достаточно большом числе n, приближенно равна:

где 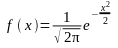– функция Гаусса и

Приближенные значения вероятности Рmn, задаваемые локальной формулой, на практике используются как точные при условии npq > 20.

Значения функции Гаусса приведены в табл. I приложений.

1. Функция f(x) является четной, т.е. f(-x) = f(х).

2.Функция f(x) – монотонно убывающая при положительных значениях х, причем при х → ∞ f(x) → 0 (практически можно считать, что уже при х > 4 f(x) ≈ 0.

Интегральная теорема Муавра—Лапласа.

Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от а до b (включительно), при достаточно боль-шом числе n приближенно равна:

где 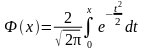- функция Лапласа (интеграл вероятностей);

При выполнении условия npq > 20 интегральная формула дает, как правило, удовлетворительную для практики погреш-ность вычисления вероятностей.

Значения функции Лапласа приведены в табл. II приложений.

1. Функция Ф(x) является нечетной, т.е. Ф(-x) = - Ф(х).

2. Функция Ф(x) – монотонно возрастающая, причем при х → ∞ Ф(x) → 1, практически можно считать, что уже при х > 4 Ф(x) ≈ 1.

Следствия.

Если вероятность р наступления события А в каждом испыта-нии постоянна и отлична от 0 и 1, то при достаточно большом числе n независимых испытаний вероятность того, что:

а) число m наступлений события А отличается от произведения nр не более, чем на величину ε > 0 (по абсолютной величине):

б) частость m /n события А заключена в пределах от α до β(включительно):

в) частость m /n события А отличается от его вероятности р не более, чем на величину Δ > 0 (по абсолютной величине):

9)Случайная величина и ее закон распределения. Дискретные и непрерывные случайные величины.

Случайной называется величина,которая в результате испытания может принять то или иное значение из некоторой совокупности своих возможных значений, причем заранее неизвестно какое именно.

Случайные величины:

а) непрерывные (число возможных значений несчетно);

б) дискретные (число возможных значений конечно или счетно);

в) смешанные(примером смешанной случайной величины может служить заработок рабочего,пропорциональный его выработке,но не меньший гарантированного размера оплаты).

Случайной величиной X называется функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий), т.е.

X = f(ω),

где ω—элементарный исход(или элементарное событие,принадлежащее пространству Ω, т.е.).

Пример.Случайная величина X – число дней во взятом наудачу месяце года есть функция элементарных исходов (событий) ω испытания — розыгрыша (выбора наудачу) месяца года.

Для дискретной случайной величины множество возможных значений случайной величины, т.е. функции f(ω), конечно или счетно, для непрерывной — несчетно.

Законом распределения случайной величины называется правило (соотношение), устанавливающее связь между, возможными значениями случайной величины и соответствующими им вероятностями.

ЗАКОН РАСПРЕДЕЛЕНИЯ ЗАДАЕТСЯ

для дискретных случайных величин:

- аналитически (в виде формулы);

- таблично (ряд распределения);

- графически (многоугольник или полигон распределения);

для непрерывных случайных величин:

- функцией распределения.

Функцией распределения случайной величины Х называется функция F(x) выражающая для каждого х вероятность того, что в результате опыта случайная величина Х примет значение, меньшее х:

F( x) = P( X < x).

СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ:

1. Значения F(x) лежат в интервале от 0 до 1, то есть 0 ≤ F(x) ≤ 1.

2. Функция распределения F(x) - неубывающая функция своего аргумента,

то есть если Х два больше х один, то F(x два)большеF(x один) .

3. Функция распределения равна нулю при х=-бесконечность и единице при х=+бескончность .

4. Вероятность попадания случайной величины в интервал [х₁ , х₂ ) равна

приращению ее функции распределения на этом интервале, т.е.

Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой про-исходят в точках, соответст-вующих возможным значениям случайной величины и равны вероятностям этих значений.

Сумма всех скачков функции F(x) равна 1.

Плотностью вероятности (плотностью распределения или просто плотностью) f(x) непрерывной случайной величины X называется производная ее функции распределения:

СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ:

1. Плотность распределения - неотрицательная функция, f(x) ≥ 0.

2. Вероятность попадания непрерывной случайной величины в интервал [а, b] равна определенному интегралу от ее плотности вероятности в пределах от а до b:

3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:

Случайная величина X называется н е п р е р ы в н о й, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.

Следствие. Если X – непрерывная случайная величина, то вероятность попадания случайной величины в интервал (x1,x2) не зависит от того, является этот интервал открытым или закрытым, т.е.

Математические операции над случайными величинами

Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина.

Произведением kХ случайной величины X на постоянную величину k называется случайная величина, которая принимает значения kxj с теми же вероятностями pi (i = 1, 2, ..., n).

m-й степенью случайной величины X, т.е. X^m , называется случайная величина, которая принимает значения с теми же вероятностями pi (i = 1, 2, ..., n).

Суммой (разностью или произведением) случайных величин X и Y называется случайная величина, которая принимает все возможные значения вида xi +yj (xi – yj или xi ∙yj), где i =1,2,...,n; j =1,2,...,m, с вероят-ностями рij того, что случайная величина X примет значение хi a Y – значение уj :

10)Основные законы распределения случайных величин: равномерное, Бернулли, Пуассона, экспоненциальное, нормальное.

1)равномерное распределение

Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [а, b], если ее плотность вероятности f(х) постоянна на этом отрезке и равна нулю вне его, т.е.

Теорема.

Математическое ожидание и дисперсия случайной величины X, распределенной по равномерному закону, есть соответственно:

2)распределение Бернулли(биномиальное)

Дискретная случайная величина X имеет биномиальный закон распределения (распределение Бернулли) с параметрами n и р, если она принимает значения 0,

1, 2,..., m,..., n c вероятностями

где 0 < p < 1, q = 1 — p.

Теорема.

Математическое ожидание случайной величины X, распределенной по биномиальному закону и ее дисперсия равны соответственно

3)распределение Пуассона

Дискретная случайная величина X имеет закон распределения Пуассона с параметром λ > 0, если она принимает значения 0, 1, 2 ,..., n,(бесконечное, но счетное множество значений) с вероятностями

Теорема.

Математическое ожидание и дисперсия случайной величины,распределенной по закону Пуассона, совпадают и равны параметру X этого закона, т.е.

4)показательное(экспоненциальное) распределение

Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром λ > 0, если ее плотность вероятности

имеет вид:

Теорема. Математическое ожидание дисперсия случайной величины X, рас-пределенной по показательному (экспоненциальному) закону, есть

5)нормальное распределение

Открытие данного закона (впоследствии Жюль Анри Пуанкаре (1854–1912) назвал его нормальным законом распределения вероятностей) связано с именами трех ученых, которые открыли его почти одновременно.

Малоизвестный математик из Америки Роберт Адриан Эдрейн (1775–1843) опубликовал свои результаты в 1808 г., великий немецкий математик Карл Фридрих Гаусс (1777–1855) сделал свое открытие годом позже, а знаменитый французский математик Пьер-Симон маркиз де Лаплас (1749–1827) изложил свои исследования в книге "Аналитическая теория вероятностей" в 1812 г.

непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами a и σ², если ее плотность вероятности имеет вид:

Теорема. Математическое ожидание случайной величины X, распределенной по нормальному закону, равно параметру а этого закона, т.е. М(Х) = а, а ее дисперсия — параметру σ², т.е. D(X) = σ².

Нормальный закон распределения случайной величины с параметрами а = 0, σ² = 1, т.е. N(0;1), называется стандартным или нормированным, а соответствующая нормальная кривая — стандартной или нормированной.

Теорема. Функция распределения случайной величины X, распреде-ленной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:

СВОЙСТВА НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

1. Вероятность попадания случайной величины X, распреде-ленной по нормальному закону, в интервал [х1, х2], равна

2. Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания а не превысит величину Δ > 0 (по абсолютной величине), равна

«Правило трех сигм»

Если случайная величина X имеет нормальный закон распределения с параметрами а и σ², т.е. N(a;σ²), то прак-тически достоверно, что ее значения заключены в интервале (а - Зσ, а + Зσ ).

Коэффициент асимметрии A = μ3 / σ³ и эксцесс нормального распределения E = μ4 / σ⁴ – 3 равны нулю, т.е. крутость и скошенность других распределений определяется по отношению к нормальному.