5.6Разложение функции только по синусам или косинусам

Пусть функция f	определена на отрезке [0, T ]. Для простоты бу-
дем считать, что она кусочно дифференцируема на [0, T ]. Рассмотрим
функцию
f(x) =			f(x), x [0, T ],
e		f( x), x			[	−	T, 0).

Она является четной и на промежутке (0, T ] обладает дифференциальными свойствами функции f, причем fe0(x) = f0(x) в тех точках x из (0, T ), в которых f дифференцируема. Если функция f дифференцируема в точке x0 (0, T ], то по теореме о дифференцируемости суперпозиции функция fe дифференцируема в точке −x0 [−T, 0) и

fe0(−x0) = (f(−x))0x=x0 = −f0(−x0).

Если в точке x0 (0, T ) функция f не дифференцируема, но существуют конечные предельные значения f0(x0 ± 0), то существуют конечные пределы:

lim

f0

(

x

lim

f0

(

x

) =

f0

(

x

,

x→x0±0

e

) = x→x0±0

0 ± 0)

и

lim f0(−x) = −f0(−x0 0).

x→x0±0

Всилу сказанного, функция fe кусочно дифференцируема на [−T, T ],

азначит, учитывая ее четность,

f(x)

a0

∞

kπx

где

+

ak cos

,

2

T

e

=1

kX

1

T

kπx

2

T

kπx

ak =

Z

f(x) cos

dx =

Z

f(x) cos

dx,

T

T

T

T

−T

e

0

и полученный ряд Фурье сходится в каждой точке x R, его сумма S(x) является 2T -периодической функцией и

f(x + 0) + f(x − 0)

,

x

( T, T )

S(x) =

e

2

e

−

f(T

−

0) + f( T + 0)

, x = ±T.

e

2 e

−

Поскольку

f

lim f(x) = f(+0), f(

−

0) = lim f(

−

x) =

lim f(x) = f(+0),

e(+0) = x→+0

e

x→−0

x→+0

то S(0) = f(+0). А так как

f

T

lim

f( x) = lim

f(x) = f(T

−

0),

e(−

+ 0) = x→−T +0

−

x→T −0

165

x→T −0

lim

fe(T − 0) = f(x) = f(T − 0),

то S(T ) = S(−T ) = f(T − 0).

Следовательно, S(x) = f(x) в точках непрерывности функции f, содержащихся в [0, T ], и потому в них функция f разлагается в полу-

ченный ряд Фурье, содержащий только функции cos			kπx	, k N0.
			T
В случае T = π функции f разлагается в классический ряд Фурье
только по cos kx, k N.
С помощью функции
f(x) =		f(x), x (0, T ),
		0, x = 0, x = T,
		±
e		−f(−x), x (−T, 0),

которая является нечетной, аналогично рассуждая, можно получить разложение функции f в ряд Фурье только по функциям sin kπxT , k N

(соответственно, по sin kx, k N, если T = π), в точках непрерывности функции f, содержащихся в (0, T ). К этим точкам можно присоединить точки 0 и T , если в них функция f равна нулю.

Пример 5.3. Функцию f(x) = x разложить по косинусам кратных

дуг на отрезке [0, π].
Пусть		x, x [0, π],
f(x) =
e		x, x		[	π, 0).
	−			−
e				e	является четной, 2π—перио-
Тогда f(x) = |x|, x [−π, π], и функция				f

дической, непрерывной, кусочно дифференцируемой. Поэтому для всех

	a0		∞
e			kX
x [−π, π] имеет место равенство f(x) =	2	+	ak cos kx, в котором
			=1

2 Zπ

a0 = π 0 x dx = π .

1

π

2

π

2

π

ak =

Z

f(x) cos kx dx =

Z

f(x) cos kx dx =

Z

x cos kx dx =

π

π

π

−π

e

0

0

2

k

0

, k = 2n,

−

−

, k = 2n 1, n

N

.

πk

2

=

2

(( 1)

1) =

4

−

−π(2n − 1)

Так как fe(x) = f(x) для всех x [0, π], то

π

∞

4

nX

f(x) = x =

2 −

−

1)2 cos(2n − 1)x,

x [0, π].

=1 π(2n

166

Заметим, что f(0) = 0, поэтому 0 =							π	∞	4	. Отсюда
								− =1
							2		π(2n 1)2
	π2		= ∞	1				nX	−
следует, что						.
		8		(2n	2
			=1		1)
				−
			nX

Пример 5.4. Найти и исследовать на сходимость ряд Фурье 2π— периодической функции

f(x) = − ln | sin x2 |, x 6= 2πk, k Z.

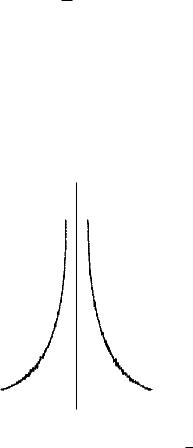
Прежде всего заметим, что данная функция является четной, 2π-пе- риодической, дифференцируемой на R \ {2πk, k Z}, а, значит, и на множестве G0 = [−π, 0) S(0, π], абсолютно интегрируемой на [−π, π]. Ее график на множестве G0 имеет вид, представленный на рисунке 5.1.

y 6

					-
		0	π		x
−π

Рис. 5.1: График функции y = − ln | sin x2 |.

Поэтому для всех x G0, а в силу 2π—периодичности, для всех x 6= 2πk, k Z,

f(x) =

a0

+

∞ an cos nx где

2

nX

=1

2

π

x

2

π/2

x

2

π

x

a0 = −

Z

ln sin

dx = −

Z

ln sin

dx −

Z

ln sin

dx =

π

2

π

2

π

2

0

0

π/2

2

π/2

x

2

π/2

x

2

π/2

1

= −

Z

ln sin

dx −

Z

ln cos

dx = −

Z

ln(

sin x) dx =

π

2

π

2

π

2

0

0

0

2

π/2

1

π

t

a

= ln 2 −

Z

ln sin x dx = ln 2 −

Z

ln sin

dt = ln 2 +

0

.

π

π

2

2

0

0

167

Таким образом, a0 = 2 ln 2. Далее, для всех n N,

2

π cos nx ln sin

x

2 sin nx

x

π

π

sin nx cos x2

an =

−

dx =

−

ln sin

+

dx =

π

π n

π n sin x

Z

2

2

Z

0

0

2

0

1

π

sin(n + 1 )x + sin(n

1 )x

1

π

1

Z

−

Z

=

2

2 sin x

2

dx =

(Dn(x) + Dn−1(x)) dx =

.

πn

2π n

n

0

2

−π

Здесь Dn(x) — ядро Дирихле, и для получения последнего равенства использована формула (5.12). Таким образом,

		x		∞	cos nx
	− ln | sin		| = ln 2 +	nX			,	x 6= 2πk, k Z.
		2		=1	n
	Полагая x = π, получим, что ln 2 =					∞		(−1)n−1	.
						nX
								n
						=1

5.7Разложение sin1 x и ctg x на простые дроби

Проведем разложение функции cos αx, α 6= k, k Z, в ряд Фурье на отрезке [−π, π]. Так как функция cos αx непрерывна на [−π, π], то

cos αx Rf1[−π,π]. Поскольку она дифференцируема на [−π, π] и cos απ = cos(−απ), то ее ряд Фурье сходится на [−π, π] к f(x), а его сумма яв-

ляется 2π-периодической функцией. Учитывая четность функции cos αx получаем, что

a0

∞

kX

ak cos kx, x [−π, π],

где

cos αx =

2

+

=1

2

π

1

π

ak =

Z

cos αx cos kx dx =

Z (cos(α + n)x + cos(α − n)x) dx =

π

π

0

0

=

1

sin(α + n)π

+

sin(α − n)π

=

(−1)n

sin απ

+

sin απ

=

π

α + n

α

−

n

π α + n α

−

n

=

(−1)n sin απ

1

+

1

n

=

(−1)n 2α sin απ

, n

N0

,

π

α + n α

π (α2

n2)

то есть

−

−

−

(α2

n2)

−

π

α

cos αx =

sin απ

1

+

∞ (

1)n

2α

cos nx , x

[

π, π]. (5.19)

nX

−

=1

В частности, если x = 0, то

1 = sin απ

1

+

∞ (

1)n

2α

,

απ

π(α2

n2)

nX

−

−

=1

168