28

значительные изменения скорости в латеральном направлении – тогда коэффициентом элемента тонкой линзы нельзя пренебречь.

Как рассматривается в Разделе 4.3.2, на практике 15-градусная конечноразност- ная миграция может с достаточной точностью оперировать наклонами до 35°. Здесь представлены круто-наклонные аппроксимации к скалярному волновому уравнению приведенные к одинарному времени пробега. Уравнение для 45° и его распространение на более крутые наклоны рассматривается в Приложении С.3, а практические аспекты миграции крутых наклонов излагаются в Разделе 4.3.4. Конечноразностные алгоритмы для крутых наклонов удобнее реализовать в частотно-пространственной области, чем в пространственно-временной области.

Для решения дифференциальных уравнений требуются граничные и начальные условия. Начальным условием для миграции является зарегистрированное на поверх- ности волновое поле (z = 0). В миграции мы также предполагаем, что волновое поле равно 0 после максимального времени наблюдения, обычно после конечного времени зарегистрированной трассы. Затем имеются боковые границы, вне которых необходимо сделать допущение о форме волнового поля.

В координатах (x, z, t) сейсмический разрез представлен плоскостью (x, t), а миг- рированный разрез – плоскостью (x, z). Как рассматривается здесь, конечноразностная миграция экстраполирует плоскость (x, t) конечными приращениями z и выводит вол- новое поле при t = 0 на каждом шаге (рис.4.31). Другой метод миграции, известный как обратная миграция во времени (reverse time migration) (Baysal и др., 1983), экстраполи- рует первоначальную нулевую плоскость (x,z) назад во времени, которая в сейсмиче- ских данных P(x,z = 0,t) исполняет функцию граничного условия (при z =0) на каждом временном шаге. На времени t = 0 эта плоскость (x,z) содержит результат миграции

P(x,z,t = 0) (рис.4.32).

Оба подхода, Кирхгоффа и конечноразностной, основываются на одном и том же скалярном волновом уравнении. Они различаются только с точки зрения решения этого уравнения. Миграция Кирхгоффа основана на интегральном решении, конечно- разностная миграция – на дифференциальном решении. Независимо от метода все ме- тодики миграции включают принцип получения изображения. Одно важное преимуще- ство конечноразностных методик перед другими методами миграции состоит в их спо- собности лучше оперировать изменениями скоростей в латеральном направлении.

4.2.3 Пространственная миграция

(Frequency-Wavenumber Migration)

Stilt (1978) ввел в миграцию методы преобразования Фурье. С этого времени появился ряд статей по теории и о практической стороне пространственной миграции. Gazdag (1978) опубликовал свою работу о методе смещения по фазе, которая привела к дальнейшему пониманию экстраполяции волнового поля в области преобразования. Пространственная миграция (f-k-миграция) с физической точки зрения объясняется не так просто, как миграция Кирхгоффа или конечноразностная миграция. Chun и Jacewitz (1981) позволили взглянуть внутрь основ пространственной миграции.

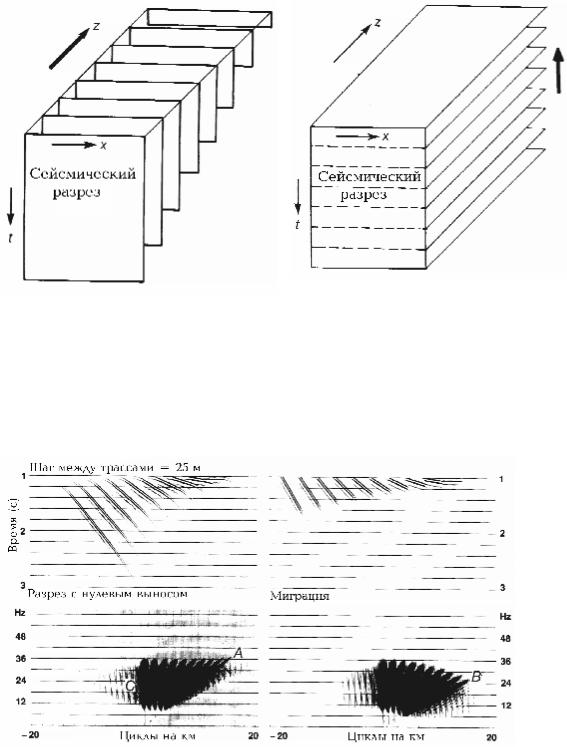
29

Рис.4.31 Сейсмический разрез, представленный плоско-	Рис.4.32 Обратная миграция во времени: начинаем с
стью (x, t) на поверхности (z = 0), может быть продолжен	плоскости (x,z) на дне куба данных и экстраполируем в
вниз с целью получения временных разрезов на дискрет-	направлении t = 0, чтобы рассчитать мгновенные кадры
ных уровнях глубин. Направление экстраполирования	плоскости (x,z) на различных временах. Эти мгновенные
обозначено толстой стрелкой. Мигрированный разрез	кадры обозначены горизонтальными плоскостями; на-
представлен плоскостью (x,z) на времени t =0 (принцип	правление экстраполяции показано толстой стрелкой. На
получения изображения).	каждом временном уровне в плоскости (x,z) из сейсми-
	ческого разреза включает граничную величину (срез х
	при t = 0 – обозначено пунктирной линией). Мигриро-
	ванный разрез представляет собой плоскость (x,z) при t =
	0 (верхняя горизонтальная плоскость).

Рис.4.33 Миграция наклонной отражающей поверхности в областях (t,x) (вверху) и (f,k) (внизу). Энергия А, ассоции- рованная с наиболее сильным наклоном, после миграции попадает в В. С упоминается в упражнении 4.14. Скорость

всреде постоянная и равна 3500м/с.

ВРазделе 1.6 мы видели, что отражения от наклонных ОП в пространстве (t,x)

попадают в область f-k в виде радиальных линий. Чем больше угол падения ОП, тем ближе радиальная линия к оси волновых чисел. На рис.4.33 дается пространственное представление отражений от наклонных ОП до и после миграции. Обратите внимание,

что миграция поворачивает радиальные линии в двумерном амплитудном спектре от оси нулевого волнового числа. Это вращение напоминает открывание конуса. Отраже-

Рис.4.34 Миграция в области (f,k). (а) Наклонная

отражающая поверхность представлена радиальной линией ОВ в плоскости (f,k). (b) После миграции

радиальная линия ОВ попадает на другую линию ОВ′, а В попадает на В′. Горизонтальное волновое число при миграции не изменяется. Для сопостав- ления f-k-отклик отражения от наклонной поверх- ности до миграции (а) наложен на отклик после миграции (b). (Chun и Jacewitz, 1981.)

30

ние от самой крутой ОП, представленное радиальной линией А, после миграции попа- дает на радиальную линию В.

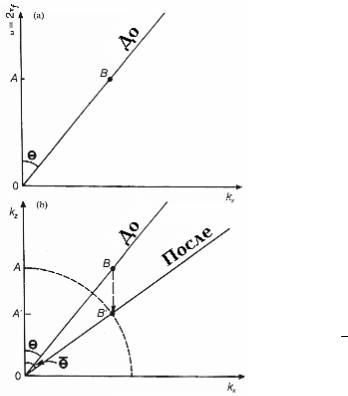
Миграция отражения от наклонной поверхности в области f-k показана на рис.4.34. Вертикальная ось – это ось частот ω для отражения до миграции; это верти- кальное волновое число kz, ассоциирован- ное с осью глубин для мигрированного от- ражения. Данный рисунок является про- странственным эквивалентом рисунка 4.14. На обоих рисунках мы предполагаем, что скорость равна 1. Пространственная мигра-

ция размещает линии постоянной частоты АВ на плоскости (ω,kx) в точки АВ′ на плос- кости (kz,kx). Следовательно, миграция пе-

реносит точку В по вертикали в точку В′. В

этом процессе горизонтальное волновое число kx не изменяется в результате мигра- ции. После окончания миграции, отражение

ОВ от наклонной поверхности становится ОВ′; следовательно, угол падения после ми- грации (θ ) больше, чем до миграции (θ).

Для сравнения эти две радиальные линии показаны на одной и той же плоскости

(kz,kx).

Сейчас мы исследуем годограф ди-

фрагированной волны и его сжатия в точку миграции в f-k-области. На рис.4.35 показан годограф дифрагированной волны в облас- тях (t,x) и (f,k). Предположим, что годограф

состоит из последовательности наклонных участков А, В, С, D, Е. Участок

А с нулевым наклоном находится на вершине гиперболы, а участок Е с наибольшим наклоном расположен вдоль асимптоты. В пространстве (f,k) участок А располагается вдоль оси частот, а наклонные участки В, С, D – вдоль радиальных линий, постепенно удаляющихся от оси частот. Участок Е располагается вдоль радиальной линии, которая представляет границу между областями распространения и исчезновения. Область ис-

чезновения соответствует энергии, которая расположена при угле 90° от вертикали или больше. Противоположная сторона гиперболы попадает во второй квадрат плоскости f- k, где kx имеют отрицательные значения.

Анализ, приведенный на рис.4.35, основан на представлении гиперболы в виде последовательности отдельных наклонных участков. В непрерывном случае гипербола представляется в виде конуса в области частот. Миграция раскрывает этот конус, как показано на рис.4.36.

Мы ожидаем, что миграция сожмет гиперболу в точку на ее вершине. Спектр этого мигрированного разреза в действительности должен походить на спектр, пред- ставленный на рис.4.37, где он имеет форму прямоугольника. Почему возникает разли- чие между этим спектром и спектром после миграции на рис.4.36?

Если мы начнем с точки и смоделируем ее, получим гиперболу на рис.4.37. В действительности же мы имеем дело с гиперболой, показанной на рис.4.36. Эти две ги-

31

перболы в области (t,x) не выглядят разными, но обратите внимание на различие их пространственных спектров. F-k-спектр реальной дифрагированной волны, который всегда подвергается полосовой фильтрации (рис.4.36), теряет энергию приблизительно над линией 42Гц, тогда как на f-k-спектре смоделированной дифрагированной волны (рис.4.37) такая энергия присутствует. Эта потеря высоких частот и обуславливает раз- личие между спектрами после миграции.

Математический вывод методик пространственной миграции дается в уравнении (С.4). На рис.4.38 показана блок-схема метода смещения по фазе; ее обоснование при- водится в Приложении (С.7). Продолжение вниз включает чистую операцию смещения по фазе exp (-ikzz). На каждом шаге z рассчитывается новый оператор экстраполирова- ния со скоростью, определенной для этой величины z. Как и для любой другой мигра- ции, на каждом шаге экстраполирования нам необходимо привлекать принцип получе- ния изображения (t = 0), чтобы получить мигрированный разрез. Для выполнения усло- вия получения изображения t = 0 необходимо выполнить суммирование экстраполи- руемого волнового поля по всем частотным составляющим на каждом шаге глубины.

Это можно видеть из интегрального представления обратного преобразования Фурье экстраполированного волнового поля [см. уравнение (С.52)]. Процедура продолжения вниз и получения изображения повторяется до тех пор, пока все волновое поле не будет мигрировано.

Рис.4.35 Гипербола попадает на треугольный участок на плоскости (f,k) (подробности в тексте).

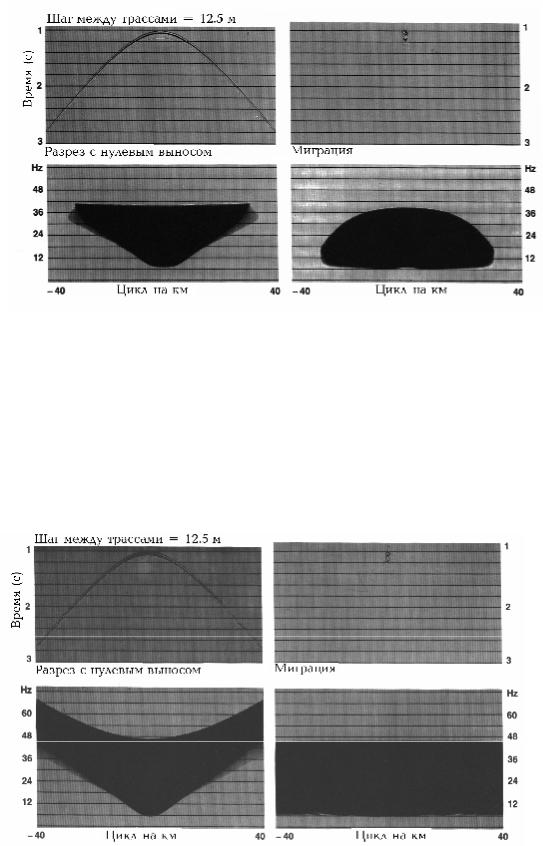
32

Рис.4.36 Дифрагированная волна и ее миграция в областях (t,x) (вверху) и (f,k) (внизу).

Метод смещения по фазе (Gazdag, 1978) может оперировать только скоростями, изменяющимися в вертикальном направлении. Gazdag и Squazzero (1984) расширили этот метод так, чтобы можно было оперировать изменениями скоростей в латеральном направлении. Для этого входное волновое поле сначала экстраполируется методом смещения по фазе с применением ряда скоростных функций, не изменяющихся в лате- ральном направлении; создается последовательность опорных волновых полей. Затем рассчитывается волновое поле путем интерполяции из опорных волновых полей. Этот метод миграции известен как смещение по фазе плюс интерполяция (phase-shift- interpolation).

Рис.4.37 Миграция дифрагированной волны в областях (t,x) (вверху) и (f,k) (внизу). В реальности такие гиперболы не встречаются; мы имеем дело с гиперболами через полосовой фильтр (рис.4.36). Обратите внимание на различие ам- плитудных спектров двух гипербол.

33

Если скорость в среде постоянная, эта миграция может быть выражена как пря- мой переход от изменения частоты во времени ω к вертикальному волновому числу kz (Stolt, 1978) (рис.4.34). На рис.4.39 приведена блок-схема алгоритма Stolt; см. также Приложение С.4.

Эффективность алгоритма Stolt для постоянной скорости объясняется прямым переходом, который дается уравнением (С.35). Однако для расчета соответствующей ω для данных величин kx и kz алгоритм включает интерполяцию в пространстве (f,k). Во- прос в том, имеет ли этот метод, какую-либо практическую ценность, поскольку в ре- альности разрезов с постоянной скоростью не бывает.

Stolt расширил свой метод для оперирования изменениями скоростей (Приложе- ние С.4). Для случая изменяющейся скорости расширения Stolt включает (1) модифи- цирование входного волнового поля таким образом, чтобы оно выглядело как отклик разреза с постоянной скоростью; (2) применение алгоритма, использующего постоян- ную скорость (см. рис.4.39); (3) обращение первоначальной модификации входного волнового поля. Эта модификация, в сущности, представляет собой тип растяжения оси времен (см. Приложение С.4), который позволяет сделать времена отражений прибли- зительно эквивалентными временам, зарегистрированным для разреза с постоянной скоростью. Характер растяжения описан так называемым коэффициентом растяжения W. Случай постоянной скорости эквивалентен W=1. На практике алгоритм постоянной скорости используется в остаточной миграции (Раздел 4.3.3 и Приложение С.5).

Обычно результаты миграции со смещением по фазе и миграция Stolt отобра- жаются в полном вертикальном времени пробега τ = 2z/v (аналогично результатам ко- нечноразностной миграции и миграции Кирхгоффа). На практике размещение в f-k- области происходит из (ω,kz) в (ωτ,kx), а не в (kz,kx), где ωτ - двойное преобразование Фурье τ и представляет собой kz, умноженное на v/2. Уравнения (С.52) и (С.55) могут быть выражены соответственно для методов Stolt и смещения по фазе в единицах τ, а не z; для этого вместо уравнения (С.53) используется уравнение (с.38а).

Из анализа, приведенного выше, следует важная концепция. Из уравнения (С.38а) мы видим, что для постоянной kx ω>ωτ; следовательно, миграция смещает поло- су пропускания в сторону низких частот. Это аналогично заключению, сделанному по отношению к поправке за нормальное приращение, т.к. она также обуславливает рас- тяжение данных в сторону низких частот (Раздел 3.2.2).