12

лучить зону обнуления, как показано на рис.3.15b. На рис.3.15с показан результат не- удачного выбора обнуления, обоснованный на селекции по входной выборке (рис.3.15а). Избыточное обнуление может быть опасным. На больших выносах часто бывает необходимо эффективно подавить кратные отражения. Сходную процедуру можно использовать для определения внутреннего обнуления. На этот раз кратность суммирования увеличивается в направлении ближних выносов.

3.2.3 Нормальное приращение для наклонного слоя

На рис.3.16 показан один наклонный слой. Мы хотим рассчитать время пробега от источника S до точки D на отражающей поверхности и до сейсмоприемника G. Для наклонного слоя средняя точка М больше не представляет собой вертикальную проек- цию глубинной точки на поверхность. Термины выборка ОГТ и выборка ОСТ равно- значны только для горизонтально-слоистого разреза. Когда имеется наклон отражаю- щей поверхности (ОП) или изменение скорости в латеральном направлении, две вы- борки различаются между собой. Средняя точка М остается общей для всех пар источ- ник – сейсмоприемник в пределах выборки независимо от наклона. Глубинная точка D различается для каждой пары источник – сейсмоприемник в выборке ОСТ, зарегистри- рованной по наклонной ОП. Используя геометрические построения, показанные на рис.3.16, Levin (1971) вывел следующее уравнение полного времени пробега в двух из- мерениях для слоя, наклоненного под углом φ:

t2(x) = t2(0) + x2cos2φ/v2

(3.7)

Это снова уравнение гиперболы, но сейчас скорость нормального приращения определяется как скорость в среде, деленная на косинус угла наклона:

vNMO = v/cosφ

(3.8)

Для надлежащего суммирования сигнала от наклонной поверхности требуется скорость, которая больше скорости в среде над ОП. Levin распространил свои исследо- вания на наклонную плоскую поверхность в трехмерном пространстве, как показано на рис.3.17. В этом случае скорость нормального приращения зависит не только от накло- на поверхности, но и от азимута линии, соединяющей источник и сейсмоприемник:

vNMO = v/(1 – sin2 φ cos2 θ)1/2

(3.9)

Азимут θ - это угол между направлением структурного падения и направлением профиля (рис.3.17).

Кажущийся угол падения определяется как:

sin φ′ = sin φ cos θ

(3.10)

Используя это определение, скорость нормального приращения, задают уравне- нием (3.8), можно переписать как:

vNMO = v/ cos φ′

(3.11)

Это уравнение идентично уравнению (3.8) для, наклонного слоя в двумерном пространстве. Исключением является то, что уравнение (3.11) относится к кажущемуся наклону, а уравнение (3.8) – к истинному наклону.

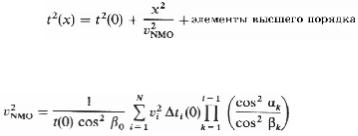
13

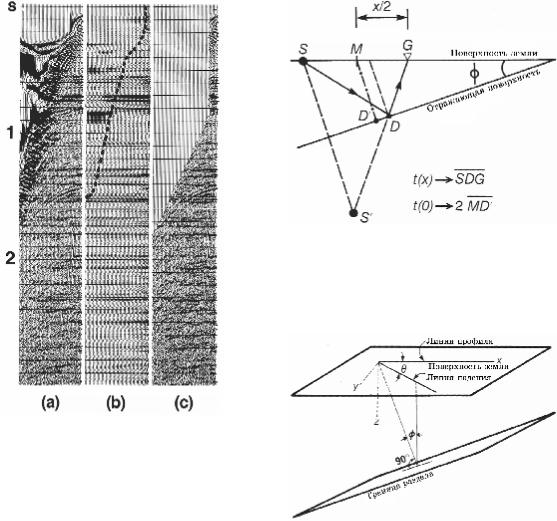
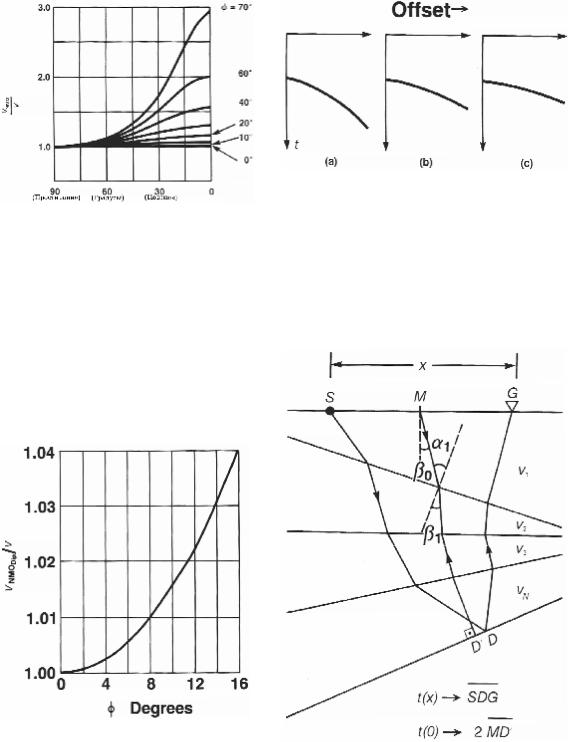
Levin (1971) построил отношение vNMO/v [уравнение (3.9)] в функции наклона и азимута. Результаты представлены на рис.3.18. Горизонтальная ось – азимут. Когда профиль направлен по падению, азимут равен нулю; когда профиль направлен по про- стиранию, азимут равен 90°. Отношение vNMO/v принимает большое значение, когда профиль отстрелян в направлении структурного падения или близко к нему. Levin (1971) построил также отношение vNMO/v по линии падения в функции малых углов структурного падения. Результат представлен на рис.3.19. Когда наклон не превышает 15°, отношение vNMO/v близко к единице. Для угла, равного 15°, разность между vNMO и v равна 4%.

В заключении отметим, что скорость нормального приращения для наклонного слоя (в двух или трех измерениях) зависит от угла наклона. Горизонтальный слой с вы- сокой скоростью может давать такое же приращение, как наклонный слой с низкой скорост. Это показано на рис.3.20.

3.2.4 Нормальное приращение для нескольких слоев с произвольными наклонами

На рис.3.21 приведены двумерные геометрические построения для разреза, со- стоящего из ряда слоев, каждый из которых характеризуется произвольным наклоном. Мы хотим рассчитать время пробега от источника S до глубинной точки D и до сейс- моприемника G; М –средняя точка. Луч ОСТ от средней точки М падает на наклонную поверхность по нормали (D′), причем D′ - это не то же самое, что D. Вертикальное вре- мя – это полное время пробега по лучу от М к D′. Hubral и Krey (1980) вывели выраже- ние для времени пробега t(x) вдоль SDC:

(3.12)

где скорость нормального приращения равна:

(3.13)

Углы определены на рис.3.21. Для одного наклонного слоя уравнение (3.13) сво- дится к уравнению (3.8). Для горизонтально-слоистого разреза уравнение (3.13) сводит- ся к уравнению (3.4). Пока углы наклона являются незначительными, а расстановка – короткой, уравнение пробега можно аппроксимировать гиперболой [уравнение (3.5)], а скорость, требуемая для поправки за нормальное приращение, можно аппроксимиро- вать функцией среднеквадратичной скорости [уравнение (3.4)].

В таблице 3.3 приводятся скорости нормального приращения, полученные по различным моделям разреза.

После аппроксимации короткой расстановкой и малым наклоном нормальное приращение является гиперболическим для всех случаев:

t2(x) = t2(0) + x2/v2NMO

(3.14)

Следует различать скорость гиперболического нормального приращения и ско- рость суммирования, которая позволяет оптимальным образом суммировать трассы в выборке ОСТ. Гиперболическая форма используется для определения лучшего пути суммирования:

14
t2st(x) = t2st(0) + x2/v2st	(3.15)

где vst – скорость, обеспечивающая наилучшую аппроксимацию гиперболой кривой времени пробега tst(x) на выборке ОСТ в пределах длины расстановки. Эта ги- пербола не обязательно представляет собой гиперболу короткой расстановки, подразу- меваемую уравнением (3.14).

Рис.3.16 Геометрические построения для нормального приращения одной наклонной отражающей поверхно- сти [см. уравнение (3.7)].

Рис.3.15 Выбор оптимального обнуления. Начиная с
выборки ОСТ, исправленной за нормальное прираще-
ние (изображение а), получаем зону обнуления (b).
Крайняя правая трасса в этой выборке – такая же, что и
на первоначальной выборке (а). Вторая справа – сумма
двух ближайших трасс первоначальной выборки.
Крайняя левая трасса – сумма полной кратности, полу-
ченная по первоначальной выборке. Участок над пунк-
тирной линией на изображении (b) – зона обнуления.	Рис.3.17 Геометрические построения для наклонной
Изображение (с) – результат неудачного выбора обну-	плоскости поверхности, используемые при выводе
ления, основанный на селекции из первоначальной	скорости нормального приращения в трехмерном про-
выборки (а). Сравните (b) и (с).	странстве [см. уравнение (3.9)], где φ = угол наклона, θ
	- азимут угла (Levin, 1971).

15

Рис.3.18 Графическое представление уравнения приращения в 3-D пространстве, выведенное по рис.3.17, где ϕ = угол падения, θ = азимут. Ско- рость приращения идентична скорости в среде, если направление отстрела совпадает с простира- нием (θ = 90°). Наибольшее различие между ско-

ростью приращения и скоростью в среде имеет место в направлении падения (θ = 0°) при больших углах падения (Levin, 1971).

Рис.3.19 Графическое представление уравнения приращения в 3-D пространстве, выведенное по рис.3.17 для нулевого азимута (θ = 0°) и малых углов наклона (ϕ = 0°-15°) (Levin, 1971).

Рис.3.20 Приращение для низкоскоростного сигнала (а) больше, чем для высокоскоростного сигнала (b). Прира- щение для низкоскоростного сигнала вызванного наклон- ной поверхностью (с), может быть таким же, как для вы- сокоскоростного сигнала, вызванного горизонтальной поверхностью (b). Эти наблюдения являются прямым следствием уравнения (3.7).

Рис.3.21 Геометрические построения для приращения в случае наклонной границы раздела в модели разреза с произвольно наклонными слоями [см. уравнение (3.12)] (Hubral и Krey, 1980).