Chast_10_TV

При рассмотрении следующих ниже схем выбора и получении соответствующих формул используются два важных правила сложения

и умножения.

Пусть множество A , aО A содержит n элементов, множество В, bОB, — m элементов. Тогда выбор «a или b » можно осуществить n + m способами, выбор «a и b » — nґm способами.

Действительно, если мы выбираем один элемент из объединения двух множеств A и B , то существует n + m различных возможностей. Если мы выбираем один элемент из A и один элемент из B , то для первого выбора имеется n возможностей, для второго — m возможностей и число различных пар (a,b) равно nґm.

Эти формулы допускают обобщение. Так, если имеется три множества A , aО A , B , bОB , C , c ОC , содержащие соответственно n , m и k элементов, то выбор «a или b или c » осуществляется n + m + k способами, выбор «a и b и c « — nґmґk способами, и т. д.

Пример: Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?

Решение: Используем правило сложения: N (A) = 17,

N (B) = 13, N (A B) = 17 +13 = 30 .

Пример: Переплетчик должен переплести 12 различных книг в переплеты красного, зеленого или коричневого цвета. Сколькими способами он может это сделать?

Решение:	Используем правило умножения:Nкниг = 12,
Nцветов = 12,	Nвариантов = 12ґ3 = 36 .

Выборки без возвращения

Пусть имеется множество A , состоящее из n элементов. Подмножество множества A (упорядоченное или неупоря-

доченное), состоящее из m элементов, где m Ј n, называется m –элементной выборкой из n –элементного множества (соответственно упорядоченной или неупорядоченной).

Рассмотрим основные возникающие ситуации.

1) Вычислим число способов упорядочения n — элементного неупорядоченного множества. Первый элемент можно выбрать n различными способами, второй — n -1 способами, третий — n - 2

11

способами,ит. д.Врезультатеполучаем nЧ(n -1)Ч(n - 2)Ч...Ч3Ч 2 Ч1 = n! — факториал числа n .

Упорядоченная n –элементная выборка из n –элементного множества называется перестановкой. Число перестановок n элементов

Pn = n!.

Пример: (Квартет) «Проказница Мартышка, Осел, Козел да косолапый Мишка затеяли играть квартет…». Как известно, музыканты решили, что для надлежащего звучания необходимо рассесться надлежащим образом. Сколько существует различных вариантов размещения?

Решение: Различные выборки отличаются друг от друга только порядком следования элементов, т. е. представляют собой перестановки. Их число P4 = 4! = 24 .

2) Рассмотрим упорядоченные m –элементные выборки из n – элементного множества, где m Ј n. Первый элемент можно выбрать n различными способами, второй — n -1 способами, третий — n - 2 способами, m –й элемент — n - m +1 способом. Всего различных

способов	nЧ	(	)	Ч1			n!
nЧ(n -1)Ч...Ч(n - m +1) =			n -1 Ч...Ч 2			=		.
	1Ч 2 Ч...Ч(n - m)						(n - m)!
Упорядоченная m –элементная				выборка из n –элементного

множества называется размещением из n по m . Число размещений из n по m :

	Anm =	n!		.
		(n - m)!

Пример: Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?

Решение: Различные выборки отличаются друг от друга составом и порядком следования элементов, т. е. представляют

собой размещения. Их число A4 = ( 6! ) = 720 = 360 .

6 6 - 4 ! 2

3) Рассмотрим неупорядоченные m –элементные выборки из n–элементного множества, где m Ј n. Число упорядоченных m – элементных выборок равно Anm . С другой стороны, среди всех упорядоченных m –элементных выборок существуют такие, которые отличаются друг от друга только порядком элементов. Одному на-

12

бору из m элементов соответствует Pm = m! способов упорядочения, поэтому одной неупорядоченной выборке соответствует Pm упорядоченных выборок, следовательно, число различных неупорядоченных m –элементных выборок из n –элементного множества в Pm раз меньше, чем число упорядоченных. Всего различных неупорядоченных выборок

Am		n!
n	=		.
Pm		m! Ч (n - m)!

Неупорядоченная m –элементная выборка из n –элементного множества называется сочетанием из n по m . Число сочетаний из

	n по m :	n!
	Cnm =		.
		m! Ч(n - m)!

Числа Cnm называются также биномиальными коэффициентами. Если рассмотреть коэффициенты при различных степенях x

n

в разложении бинома (1+ x)n = еam xm , то окажется, что am =Cnm .

m=0

Пример: У одного человека 7 книг по математике, а у второго — 9. Сколькими способами они могут обменять друг у друга две книги на две книги?

Решение: Так как порядок следования отбираемых книг не имеет значения, используем сочетания. Число способов, которыми первый человек может выбрать 2 книги:

N		= C2	=	7!	= 7Ч6 = 21.
	1
		7		2! Ч5!	2

Число способов, которыми второй человек может выбрать 2 книги:

N		= C2	=	9!	= 9Ч8 = 36.
	2
		9		2! Ч7!	2

Полное количество различных способов обмена находим по правилу произведения: N = N1 Ч N2 = 21Ч36 = 756 .

13

2. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БЕЙЕСА

2.1. Теорема сложения вероятностей

Для несовместных событий А и В вероятность суммы событий определяется аксиоматически: P(A + B) = P(A) + P(B) .

Пример: На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в переплете. Библиотекарь берет наудачу 3 учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

Решение: Рассмотрим события — A = {хотя бы один учебник в переплете},B = {ровно один учебник в переплете}, C = {ровно два учебника в переплете}, D = {ровно три учебника в переплете}. Очевидно, что:

1) события B , C и D несовместны; 2) A = B +C + D ,

P	(	A	)	= P		(	B	)	+ P C				)	+ P	(	D		)		, где P		(		B	)		= C51C102	= 45 ,
											(																C3	91
																											15
	(		)	=	C2C1				=		20	, P (D) =							C53C100		=			2		.
																				3
P C						5	10															91
					C3						91									C15
							15
										45			20		2					67
Итак, P (A) =										91 +			91 +					=		91 .
															91

Рассмотрим случай совместных событий.

Теорема сложения вероятностей для совместных событий. Если события А и В совместны, A ЧB № Ж , то P(A + B) = P(A) + P(B) - P(AB).

14

Разобьем

событие

A + B

на

несовместные

слагаемые:

A + B = A Ч W + B Ч W = A Ч(B +

)+ B Ч(A +

) =

B

A

= A Ч B + A Ч

+ A Ч B +

Ч B = A Ч B + A Ч

+

Ч B.

B

A

B

A

P (A + B) = P (AB + AB + AB) =

= P (AB) + P (AB

)+ P (

AB),

A = AB + AB, P (A) = P (AB) + P (AB),

P (AB

) = P (A) - P (AB),

аналогично, P (AB) = P (B) - P (AB), отку-

да P(A + B) = P(A) + P(B) - P(AB).

Вероятность суммы трех совместных

событий А, В и С:

)

(

)

( )

(

)

(

)

(

)

(

)

(

A + B +C

)

= P

(

+ P

- P

- P

- P

+ P

P

A

B

+ P C

AB

AC

BC

ABC

.

Пример: Ученик 6 класса Костя и его приятель, заняв выгодную позицию вблизи школьных дверей, обстреливали снежками всех выходящих девчонок. Когда дверь в очередной раз открылась, два снежка полетели в голову застывшего на пороге завуча — Маргариты Викентьевны. Какова вероятность того, что цель поражена, если известно, что Костя обычно попадает 8 раз из 10, а его приятель только 7?

Решение: Рассмотрим события: A = {попал Костя}, пал приятель}, события совместны, искомое событие

P(A + B) = P(A) + P(B) - P(AB) = 0,8 + 0,7 - 0,8Ч 0,7 = 0,94.

2.2. Условная вероятность события. Теорема умножения вероятностей

B = {по-

A + B .

Условной вероятностью события В при наличии А называется величина: P (B A) = PP((ABA)),P (A) № 0. Иначе говоря, условная вероят-

15

ность P (B A) — это вероятность события В, вычисленная при условии, что событие А произошло.

На практике формулу читают так: P (AB) = P (A) Ч P (B A) , т. е. вероятность произведения (пересечения, совмещения) двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого. Это правило называется теоремой умножения вероятностей (для классической схемы она легко доказывается).

Пример: Из урны, содержащей 4 белых и 3 черных шара, вынимают 2 шара. Найти вероятность того, что оба шара будут белыми.

Решение: Событие С = {оба шара белые}; представим С как произведение 2 событий С = A Ч B , где А = {первый шар белый}, В = {второй шар белый}.

	(		)		(		)		(			) ;	Р (А) =	4
P		AB		= P		A		Ч P		B	A			7 .

Предположим, что событие А произошло, т. е. в урне осталось 6 шаров, 3 из них белые, тогда P (B A) = 36 = 12 . Þ P (C) = 47 Ч 12 = 72 .

Событие А называется независимым от события В, если его вероятность не зависит от того, произошло событие В или нет, т. е. P (A B) = P (A) . В противоположном случае, если P (A B) № P (A) , событие А зависит от В.

Для произвольного числа событий вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место.

P (A1 Ч A2 Ч...Ч An ) = P (A1 )Ч P (A2 A1 )Ч P (A3 A1 Ч A2 )Ч...Ч P (ЧAn A1 Ч A2 Ч...Ч An-1 ).

Пример: В ящике 6 белых, 8 красных и 4 синих шара. Наудачу извлекают 1 шар без возвращения. Чему равна вероятность того, что на первом шаге появится белый, на втором — красный и на третьем — синий шар?

Решение: Событие А = {на первом шаге появится белый шар}, событие В = {на втором шаге появится красный шар}, событие

С = {на третьем шаге появится синий шар}.

P (A) = 186 = 13; P (B A) = 178 ; P (C AB) = 164 = 14 ;

16

P (ABC ) = 13 Ч 178 Ч 14 = 0,039.

Для независимых событий правило умножения вероятностей принимает простой вид: P (A Ч B) = P ( A) Ч P (B) , т. е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий. Для нескольких независимых событий

P (A1 Ч A2 Ч...Ч An ) = P (A1 ) Ч P (A2 ) Ч...Ч P ( An )	или	ж	n	ц	n
		P з	Х Ai ч		= ХP (Ai ) , т.е.
		и	i=1	ш	i=1

вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий.

Если события A и B независимы, то также независимы события A и B , A и B , A и B .

Пример: Фирма «ХаХаХа» выпустила акции и обещает своим вкладчикам несусветные дивиденды. Котировки акций каждый день меняются так, что стоимость одной акции возрастает в два раза. В понедельник, в первый день продажи акций, Пелагея Марковна, отстояв многочасовую очередь, втайне от мужа Ивана Кузьмича вложила в фирму 200 рублей из своей пенсии, надеясь к концу недели получить 12 тысяч 600 рублей чистой прибыли.

Сбудутся ли ее чаяния, если вероятность того, что лавочка не закроется, в день открытия составляла 1/10 и каждый день уменьшается в 10 раз? Найти вероятность указанного события.

Решение: Вероятность того, что фирма не	закроется
в первый день P1 = 10-1 , во второй день — P2 = 10-2	и т. д. Ве-

роятность того, что фирма просуществует целую неделю, рав-

на P = P1 Ч P2 Ч P3 Ч P4 Ч P5 Ч P6 Ч P7Ч = 10-(1+2+3+4+5+6+7) = 10-28 .

2.3. Вероятность появления хотя бы одного события

Пусть в результате опыта могут появиться n независимых в совокупности событий А1, А2,…, Аn, вероятности которых Р (А1), Р (А2),…, Р (Аn) — известны.

А—событие,заключающеесявпоявлениихотябыодногоизсобытий

А1, А2,…, Аn, А=А1+А2+ …+Аn.

A — событие, заключающееся в том, что ни одно из событий A1, A2,..., An не наступило: A = A1 Ч A2 Ч Ч An .

17

A + A = W, P (A + A) = P (W) = 1 , P (A)+ P (A) = 1 Ю P (A) = 1 - P (A),

P(A) = 1- P (A1 Ч A2 Ч Ч An ), P (A) = 1- P (A1 )Ч P (A2 )Ч Ч P (An ),

P(A1 ) = 1 - P (A1 ) = q1 ; P (A2 ) = 1- P (A2 ) = q2 ; P (An ) = 1 - P (An ) = qn ;

P(A) = 1 - q1q2...qn .

Пример: Ослик Иа-Иа к словам песенки «и-а» пытается угадать мелодию. Какова вероятность того, что это ему удастся хотя бы на 40 й раз?

Указание: а) ослиному крику соответствует сочетание нот ля-до; б) ослик пользуется основной октавой и уже проверенные парные сочетания не запоминает, но безошибочно отреагирует на подходящую.

Решение: Вероятность выбрать правильную комбинацию при одной случайной попытке p = (1 7)2 . Вероятность противоположного события q = 1- p = 48 49 . Вероятность того, что со-

четание не будет подобрано за 40 попыток P40 (A) = (48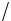49)40 . Искомая вероятность равна 1 - (4849)40 = 0,56166.

2.4. Формула полной вероятности

Следствием правил сложения и умножения вероятностей является формула полной вероятности.

Пусть проведен опыт, об условиях которого можно сделать n взаимоисключающих предположений (гипотез) H1,H2,...,Hn , образующих полную группу: H1 + H2 +... + Hn = W , Hi H j = Ж (i № j ).

Каждая гипотеза представляет собой некоторое событие. Вероятности реализации гипотез известны: Р (H1), Р (H2),…, Р

(Hn).

Результат опыта — событие А, которое может появиться только вместе с одной из гипотез, условные вероятности события А при каждой из гипотез заданы: P (A/H1), P (A/H2),…, P (A/Hn). Найдем вероятность события А, для чего представим А как сумму n несовместных событий:

n

A = H1 A + H2 A + + Hn A = еHi A.

i

18

По правилу сложения вероятностей

	ж n	ц	n
			= еP (Hi A) , P(Hi A) = P(Hi )Ч P(A	Hi ).
	P (A) = P з еHi A ч
	и i	ш	i

n

Следовательно, P (A) = еP (Hi )Ч P (A Hi ).

i

Таким образом, вероятность события А в опыте с гипотетическими условиями равна сумме произведений вероятности каждой гипотезы на условную вероятность события при условии — гипотезе.

Пример: Любимое занятие двухлетней девочки Кати — срезать пуговицы с одежды. Пока мама готовила кашу, Кате удалось отстричь все 5 белых пуговиц с папиной пижамы и 3 черные пуговицы с маминого вечернего платья. Одну пуговицу Катя проглотила, а остальные засунула в глубокую щель между полом и плинтусом. За этим занятием ее и застала мама. С большим трудом мама сумела выковырять из щели 2 пуговицы. Какова вероятность того, что платье можно привести в порядок, если одна запасная пуговица у мамы есть?

Решение: Событие A = {мама достала 2 черные пуговицы}.

Возможны две гипотезы: H1 = {проглочена белая пуговица} и

H2

= {проглочена черная пуговица}. P (H1 ) = 5 8 , P (H2 ) = 3 8 .

2

= 3Ч 2

Условные

вероятности

P (A

H1 )

= C32

= 1 ,

2

2

1

C7

7Ч 6

7

P (A

H2 ) = C22 =

=

.

7Ч 6

C

7

21

По

формуле

полной

вероятности

находим

P (A) = P (H1 )Ч P (A

H1 ) + P (H2 )Ч P (A

H2 ) = 5

Ч 1

+ 3 Ч

1

=

3

.

8

7

8

21

28

2.5. Формула Бейеса (теорема гипотез)

Формула Бейеса позволяет переоценить вероятности гипотез на основании результатов опыта. Пусть до опыта об его условиях сде-

лан ряд предположений (гипотез) H1, H2,…, Hn, гипотезы образуют
n
полную группу: еHi = W, Hi ЧH j = Ж,i № j , и известны «априорные»
i=1
(доопытные, от латинского	«a priori») вероятности:
n
P(H1 ),P(H2 ),...,P(Hn ) , еP(Hi ) =1	. В результате проведения опыта

i=1

19

произошло событие А. Найдем «апостериорные» (послеопытные, от латинского «a posteriori») вероятности гипотез: P (H1 A) , P (H2 A) ,…,

P (Hn A).

Решение: т. к. событие А может появиться только вместе

с одной из гипотез, то: P (Hi A) = P (Hi )P (A

Hi ) = P (A)P (Hi

A)

, P (Hi )P (A

Hi ) = P (A)P (Hi

A).

Разделим

на Р (А): P(Hi

A) =

P(Hi )P(A

Hi )

.

P(A)

n

По формуле полной

вероятности

P(A) = еP(Hi )P(A

Hi ),

P (Hi )P (A

Hi )

i=1

P (Hi

A) =

i = 1,2...,n.

n

еP (Hi )P (A

Hi ) ,

i=1

С помощью этой формулы возможен пересчет вероятностей гипотез после получения дополнительной информации о том, что опыт дал результат A.

Пример: Имеются три урны; в первой 1 черный и 3 белых шара, во второй — 2 белых и 3 черных, в третьей — 3 белых шара. Некто подходит наугад к одной из урн и вынимает из нее один шар. Этот шар оказался белым. Найти апостериорные («послеопытные») вероятности того, что шар вынут из 1-й, 2-й, 3 й урны.

Решение: Н1= {выбрана 1 я урна}; Н2= {выбрана 2 я урна}; Н3= {выбрана 3 я урна}. Априорные вероятности гипотез: Р

(H1) 1 = =Р (H2) = Р (H3) = 3 .

В результате опыта появляется событие А= {вынут белый шар}.

Условные вероятности события А при гипотезах Н1, Н2, Н3:

P (A H1 ) = 34 ; P (A H2 ) = 52 ; P (A H3 ) = 1. Апостериорные вероятности гипотез:

							1	Ч	3					15
P (H1		A) =					3		4				=		;
			1		3		1		2		1			43
				Ч		+		Ч		+		Ч1
			3		4		3		5		3

20