Chast_10_TV

									1	Ч	2						8
P (H2			A) =						3		5					=		;
					1		3		1		2		1				43
						Ч		+		Ч		+		Ч1
					3		4		3		5		3
									1	Ч1							20
P (H3			A) =						3						=			.
					1		3		1		2		1				43
						Ч		+		Ч		+		Ч1
					3		4		3		5		3

Таким образом, после свершения опыта и появления события А вероятности гипотез изменились. Самой вероятной оказалась гипотеза H3, наименее вероятной гипотеза H2.

21

3. ПОВТОРЕНИЕ ОПЫТОВ. ФОРМУЛА БЕРНУЛЛИ.

ПРЕДЕЛЬНЫЕ СЛУЧАИ ФОРМУЛЫ БЕРНУЛЛИ

3.1. Повторение опытов. Формула Бернулли

Рассмотрим сложный опыт, состоящий из нескольких более простых независимых опытов. В каждом из них может появиться или не появиться событие А. Опыты называются независимыми, если вероятность события А в каждом опыте не зависит от результатов других опытов.

Найдем Pn (m) — вероятность появления события A m раз в серии из n опытов. Вероятность появления события A при единичном испытании равна p , вероятность наступления противоположного события A при единичном испытании q = 1 - p . Исход серии испытаний, состоящий в том, что событие A наступило m раз и не наступило n - m раз, может реализоваться несколькими способами. Вероятность каждого такого исхода серии равна pmqn-m .

Поскольку порядок, в котором в серии появляются события A и A не существенен, число различных способов реализации m успе-

хов	в серии из n			опытов есть число сочетаний из n по m :
Cnm =		n!	.
		m!(n - m)!

Таким образом, вероятность того, что в результате n опытов событие А произойдет m раз, равна:

	Pn(m) =Cnm pmq(n-m) =	n!	pm(1	- p)n-m .
		m!(n - m)!

22

Это соотношение носит название формулы Бернулли. С ее помощью можно выразить вероятности более сложных событий: вероятность того, что в n испытаниях событие А наступит

менее m раз: Pn(0) + Pn(1) +... + Pn(m -1) ,

более m раз: Pn(m +1) + Pn(m + 2) +... + Pn(n) ,

не менее m раз: Pn(m) + Pn(m +1) +... + Pn(n) ,

не более m раз: Pn(0) + Pn(1) +... + Pn(m) .

Пример: Какова вероятность того, что при 10 бросаниях игральной кости два раза выпадут два очка?

Решение:

p= 16 , n=10, m=2, q = 1- p= 56 .

2	ж 1		ц2	ж	5	ц10-2		10!		58
P10 (2) = C10	з		ч	з		ч	=		Ч		= 0,29 .
		6			6			8!Ч 2!		10
	и		ш	и		ш				6

Пример: В мастерской 4 мотора. Вероятность нормальной работы каждого 0,9. Чему равна вероятность нормальной работы в данный момент только: a) 4 моторов; b) 3 моторов; с) 2 моторов?

Решение:

	а) P4 (4) = C44 p4q4-4 =				4!	Ч 0,94 Ч 0,10 = 0,6561	,
					4!Ч 0!
b) P4	(3) = C43 p3q4-3 =	4!	Ч 0,93 Ч 0,11 = 0,2916 ,
		3!Ч1!
c) P4	(2) = C42 p2q4-2 =	4!		Ч 0,92 Ч 0,12 = 0,0486 .
		2!Ч 2!

Если рассмотреть разложение по степеням x функции ( px + q)n , то по формуле бинома Ньютона

n

( px + q)n = еCnm pmqn-m xm = qn +Cn1 pqn-1x +Cn2 p2qn-2 x2 + ... + pn xn ,

m=0

т.е. вероятности Pn (m) являются коэффициентами при xm в разложении бинома ( px + q)n . В связи с этим совокупность вероятностей Pn

(m) называют биномиальным законом распределения вероятностей (это понятие будет обсуждаться при рассмотрении случайных величин).

23

Формула Бернулли допускает следующее обобщение. Пусть в результатеединичногоопытавозможныэлементарныеисходы A1, A2, , Ak , образующие полную группу событий и происходящие с вероятно-

стями p1, p2, , pk , p1 + p2 + + pk = 1. Вероятность того, что в серии из
n независимых испытаний событие A1 произойдет m1									раз, событие
A2 — m2 раз,…, событие Ak					— mk раз, m1 + m2 + + mk = n				, равна
P (m ,m ,...m ) =				n!		p m1	p m2	...p mk .
			m
n	1 2	k		!m ! ... m ! 1			2	k
			1	2	k

Совокупность величин Pn(m1,m2,...mk ) называют полиномиальным распределением.

3.2. Предельные случаи формулы Бернулли

Если серия состоит из большого числа испытаний, пользоваться формулой Бернулли достаточно трудно, отношение факториалов сложно вычислить с достаточной точностью. Для упрощения вычислений используются формулы, полученные из формулы Бернулли в результате предельных переходов.

3.2.1. Локальная предельная теорема Муавра — Лапласа

Если вероятность p появления события А в каждом испытании отлична от нуля и единицы (0<p<1), то вероятность P n (m) того, что при n независимых испытаниях событие А появляется m раз при n ® Ґ, удовлетворяет соотношению

Pn (m)

ѕѕѕ®1, где x = m - np ,

1

Че-

x2

j(x) =

— функция Гаусса.

2

1

2p

j(x)

n®Ґ

npq

npq

Таким образом, при больших n P n (m) »

1

j(x) .

npq

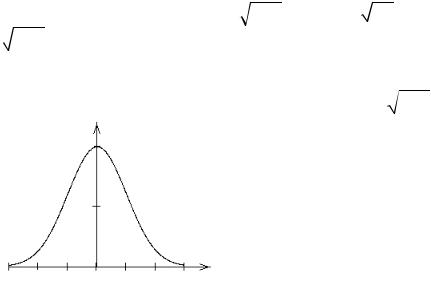
0,4

График функции Гаусса приведен на

рисунке.

Функция достаточно быстро

( )

убывает по мере удаления от начала коор-

0,2

динат — j(5) » 10-6 .

На практике локальную теорему Му-

авра-Лапласа используют, если p и q не

–3 –2 –1

0 1 2 3 малы, а npq > 9 Так, при n = 40 , m = 20 ,

p = q = 0,5 погрешность приближения со-

ставляет 0,6  %.

24

Пример: Найти вероятность того, что при 10 выстрелах мишень будет поражена 8 раз, если вероятность попадания при одном выстреле p =0,75.

Решение: P10(8) » 1 Чj(x) , npq

n = 10, p = 0,75,q = 1- 0,75 = 0,25,m = 8,

	1	=	1	= 0,730 ; x = m - np	=	8 -10 Ч 0,75	= 0,360;
	npq		10 Ч 0,75Ч 0,25			10 Ч 0,75Ч 0,25
				npq

j(0,360) = 0,374 ; P10(8) = 0,730 Ч 0,374 = 0,273 . Отметим, что даже

в таких условиях (npq<2) ошибка приближения около 3  %.

3.2.2. Интегральная предельная теорема Муавра – Лапласа

Если вероятность p события А в каждом испытании отлична от 0

	и 1 (0<p<1), то при n ® Ґ вероятность того, что событие А наступит
	в n испытаниях не менее m1 раз, но не более m2 раз,yудовлетворяет
	соотношению:						z2	( )
			1		x2
	Pn (m1,m2 ) ®				xтe	- 2 dz =Ф (x2 ) -Ф (x1 ),		–3 –2 –1 0 1 2 3 x
			2p
	1							–0,5
	где x1 = m1 - np ,						x2 = m2 - np ,
			npq				npq
		1			x		z2
	а Ф (x) =			т0 e-			2 dz — функция Лапласа.
		2p

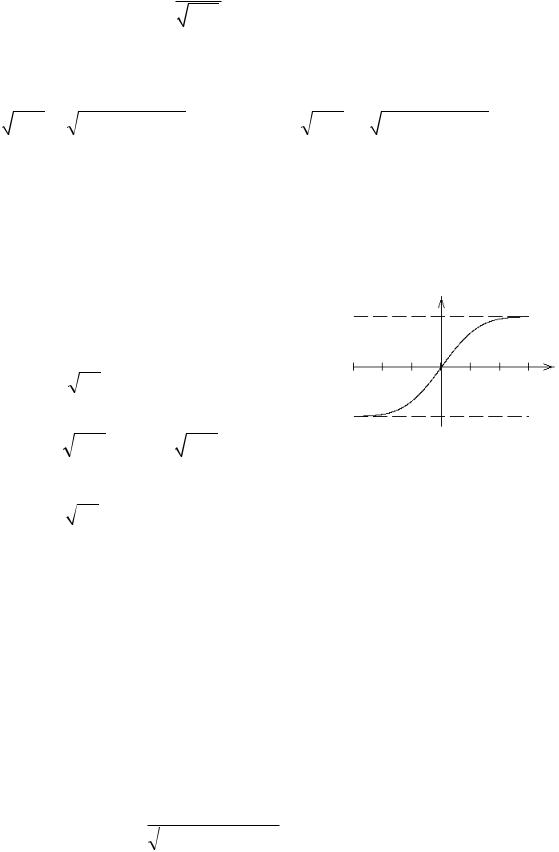
График функции Лапласа приведен на рисунке. Функция доста-

точно быстро приближается к своим асимптотам зж y = ±	1	чц	по мере
и	2	ш

2-Ф (5) » 10-6 .

Вприложении приведены таблицы значений функций Гаусса

иЛапласа. Так как первая — четная, а вторая — нечетная, значения приведены только для неотрицательных значений аргумента.

Пример: Вероятность поражения мишени при одном выстреле 0,75. Чему равна вероятность того, что при 100 выстрелах мишень1

будет поражена не менее 70 и не более 80 раз?

Решение: x1 = 70 -100 Ч 0,75 = -1,15 ; 100 Ч 0,75Ч 0,25

25

x		=	80 -100 Ч 0,75	= 1,15.Ф(x ) =Ф(-1,15) = -Ф(1,15) = -0,3749
	2
			100 Ч 0,75Ч 0,25	1

(функция Лапласа нечётна). Ф(x2 ) =Ф(1,15) = 0,3749 .

P100 (70,80) » Ф(1,15) -Ф(-1,15) = 2Ф(1,15) = 0,7498 .

3.2.3. Формула Пуассона

Если n велико, а p мало, мы имеем дело с редкими событиями, та

же вероятность	P n (m)	вычисляется приближенно по формуле
Пуассона: P n (m)	» lme-l	, где l = np . Формула Пуассона получается
	m!
из формулы Бернулли при n ® Ґ, p ® 0 , np = l = const .
На практике	пользуются распределением Пуассона, если
n і100, p Ј 0,01.

Пример: Вероятность того, что раковина содержит жемчужину, равна p = 0,01. Какова вероятность того, что в 200 раковинах най-

дется хотя бы 3 жемчужины?

Решение:

n = 200 , p = 0,01, l = np = 2 , P200 (m) = lme-l ; m!

P (A) = 1- P200 (0) - P200 (1) - P200 (2) ,

P (A) = 1- 20 e-2 - 21e-2 - 22 e-2 = 1- 5e-2 » 0,323 . 0! 1! 2!

Пуассоновское распределение возникает при рассмотрении потоков событий. Потоком событий называется последовательность однородных событий, наступающих одно за другим в случайные моменты времени (вызовы на телефонной станции, приходы покупателей в магазины и т. п.).

Среднее число событий l , приходящихся на единицу времени, называется интенсивностью потока.

1. Поток событий называется потоком без последействия, если вероятность попадания того или другого числа событий на какойто промежуток времени не зависит от того, сколько событий попало на любой другой непересекающийся с ним промежуток.

26

2. Поток событий называется ординарным, если вероятность появления на элементарном участке Dt двух или более событий пре-

небрежимо мала по сравнению с вероятностью появления одного события.

3. Если интенсивность l = const , поток называется стационарным.

Поток событий, удовлетворяющий приведенным выше трем требованиям, называется стационарным пуассоновским, или простейшим. Вероятность того, что за промежуток времени (t0,t0 + t) произойдет m событий, для простейшего потока равна

P (m,t) = (lt)m e-lt .

m!

Пример: При работе ЭВМ время от времени возникают неисправности (сбои). Поток сбоев можно считать простейшим. Среднее число сбоев за сутки равно 1,5. Найти вероятность того, что за двое суток произойдет хотя бы один сбой.

Решение: Противоположное событие — ни одного сбоя, его вероятность

P (A) = P (0,t) = (1,5Ч 2)0 e-3 = 0,05 . 0!

P (A) = 1 - P (A) = 0,95 .

27

4. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

4.1. Случайные величины. Виды случайных величин. Закон распределения случайной величины

Под случайной величиной (в дальнейшем — с. в.) понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение.

Возможные значения с. в. образуют множество X (кси), которое называется множеством возможных значений с.в.

Пример: Опыт — бросание игральной кости; с. в. Х — число выпавших очков. Множество возможных значений Ξ = {1,2,3,4,5,6}. Опыт — работа электрического устройства после ремонта; с. в. Т — время работы устройства до первого сбоя. Множество возможных значений Ξ: вся правая половина оси Оt (т.е. t³0). На практике этот участок ограничен справа, но эта граница не определена. X в этом случае несчетно. Опыт — тестирование изделий до появления первого исправного изделия. С.в. Х — число тестов, которое было проведено. Ξ = {1,2,3,…, n,…} — бесконечно, но счетно.

Если множество Ξ конечно (пр.1) или счетно (пр.3), с. в. называется дискретной (д. с.в.), если несчетно (пр.2) — непрерывной (н.с.в.).

Таким образом, с. в. Х — функция элементарного события: Х = j (w), где wЄΩ. При этом множество X возможных значений с. в. Х состоит из всех значений, которые принимает функция j (w).

28

Законом распределения с.в. Х называют правило, позволяющее находить вероятности всевозможных событий, связанных со с. в. Х (например, вероятность того, что с. в. Х примет какое-то значение или попадет на какой-то интервал).

Возможны различные способы задания закона распределения. Рассмотрим наиболее типичные.

Закон распределения д. с.в. может быть задан в виде таблицы,

n
{X = xn}… несовместны и образуют полную группу, т. о. еpi =1	. Та-
i =1	, x2 ,
первая строка которой содержит возможные значения с. в. Х: x1
…, xn , …, а вторая — вероятность этих значений p1 , p2 , …, pn …, где
pi = P (X = xi ) — вероятность того, что в результате опыта с. в. Х при-
мет значение xi (i = 1,2,...,n,...) . События {X = x1}, {X = x2}, …,

кой закон распределения называется рядом распределения. Пример: Имеется 3 независимо работающих прибора. Вероят-

ность нормальной работы 1-го равна 0,2, 2-го — 0,4, 3-го — 0,5. С.в. Х — число работающих приборов. Построить ряд распределения с.в. Х.

Решение: Возможные значения с. в. Х: 0,1,2,3. Событие «i -й

прибор работает» обозначим Ai , противоположное — Ai .

				Соответствующие вероятности:
P1 = P (X = 0) = P (A1A						2 A3 ) = 0,8Ч 0,6Ч 0,5 = 0,24,
P2 = P (X = 1) = P (A1A					2 A3 )+ P (A1A2 A3 )+ P (A1A							2 A3 ) =
= 0,2Ч 0,6Ч 0,5 + 0,8Ч 0,4 Ч 0,5 + 0,8Ч 0,6Ч 0,5 = 0,46,
P3 = P (X = 2) = P (A1A2 A3 )+ P (A1A2 A3 )+ P (A1A													2 A3 ) = 0,26,
							4								Pi
P4 = P (X = 3) = P (A1A2 A3 )
							= 0,04. еPi			=1.
								i =1
	X	0		1				2		3
	P	0,24		0,46				0,26		0,04
																	1		2		3 xi
																0
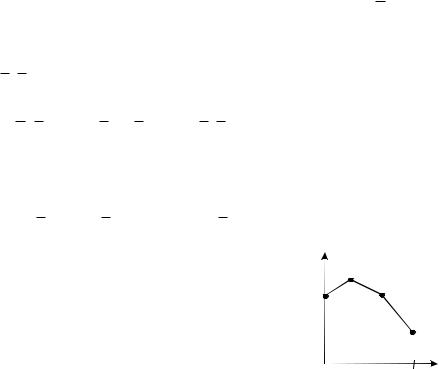
Закон распределения д. с.в. можно задать гра-

фически. Это форма задания закона называется многоугольником (полигоном) распределения. В прямоугольной системе координат строят

29

точки M1 (x1;P1 ) , M2 (x2;P2 ) ,…, Mn (xn;Pn ) , где хi — возможные значения с.в. Х, Рi — соответствующие вероятности, и их соединяют

отрезками прямых.

4.2. Функция распределения случайной величины

Общей формой закона распределения, пригодной для всех случайных величин (и дискретных и непрерывных), является функция распределения.

Функцией распределения с.в. X называется вероятность того, что с.в. X примет значение, меньшее, чем заданное х, F (x) = P (X < x). Употребляется также название интегральная функция распределе-

ния.

Геометрическая интерпретация:

	X<x	Вероятность того, что случай-
		ная точка Х попадает левее задан-
0	x	x ной точки х.

Основные свойства функции распределения:

1. F (x2 ) і F (x1 ) при x2 > x1 ;

2. F (-Ґ) = lim F (x) = 0 ;

x®-Ґ

3.F (+Ґ) = lim F (x) =1.

x®+Ґ

Функция распределения является неубывающей функцией и ее значения заключены между 0 и 1.

Вероятность того, что с. в. Х в результате опыта попадает на участок от х1 до х2 (включая х1) равна приращению функции распреде-

ления на этом участке, т. е. P {х1≤Х<х2} =F (х2) — F (х1).

Пусть точка х2 неограниченно приближается к точке х1. В преде-

ле имеем P(X = x1) = lim (F (x2 ) - F (x1)).

x ®x

Таким образом,2 1вероятность того, что с. в. Х примет значение х1, равна скачку ее функции распределения в точке х1 (если функция F (x) разрывна). Если же функция распределения непрерывна в точке х1, то эта вероятность равна 0. Если функция F (х) везде непрерывна, то вероятность каждого отдельного значения с. в. X равна 0.

Функция распределения дискретной случайной величины

Зная ряд распределения д. с.в., построим ее функцию распреде-

30