
- •А.М. Попов
- •1.1. Комбинаторика.
- •1.2. Бином Ньютона.
- •3.1. Соответствия. Функции. Отношения.
- •3.2. Подстановки.
- •3.3. Отношение эквивалентности.
- •4.1. Определения.
- •4.2. Элементарные преобразования.
- •4.3. Решение и исследование систем линейных уравнений по Гауссу.
- •4.4. Решение систем линейных уравнений по Жордану.
- •5.1. Определения. Свойства.
- •5.2. Вычисление определителей.
- •5.3. Обратная теорема об определителях.
- •5.4. Разложение определителя по столбцам.
- •5.5. Полилинейность и кососимметричность определителя по столбцам.
- •5.6. Определитель транспонированной матрицы.
- •5.7. Разложение определителя по строкам.
- •5.8. Определитель матрицы с углом нулей.
- •5.8. Теорема о полном разложении определителя.
- •5.9. Решение слу по Крамеру.
- •5.10. Теорема Лапласа.
- •6.1. Определения, примеры.
- •6.2. Простейшие свойства колец.
- •6.3. Делители нуля.
- •6.4. Кольцо классов вычетов.
- •6.5. Поля.
- •7. Линейные пространства
- •7.1. Определения, примеры.
- •7.2. Теоремы о базисах.
- •7.3. Изоморфизм линейных пространств.
- •7.4. Подпространства.
- •7.5. Теорема Кронекера-Капелли.
- •7.6. Решение однородных систем линейных уравнений.
- •8. Системы линейных уравнений
- •8.1. Определение ранга матрицы через миноры.
- •8.2. Решение систем линейных уравнений (продолжение).
- •8.3. Необходимые и достаточные условия равенства нулю определителя.
- •8.4. Общее решение неоднородной системы линейных уравнений.
- •9. Матрицы
- •9.1. Операции над матрицами, их свойства.
- •9.2. Элементарные матрицы.
- •9.3. Определитель произведения матриц.
- •9.4. Обратная матрица.
- •9.5. Решение матричных уравнений.
- •9.6. Ранг произведения матриц.
- •10.1. Построение алгебры многочленов.
- •10.2. Деление многочленов с остатком. Теорема Безу.
- •10.3. Наименьшее общее кратное и наибольший общий делитель многочленов.
- •10.4. Алгоритм Евклида.
- •10.6. Производная.
- •10.7. Кратные корни многочлена.
- •10.8. Основная теорема алгебры.
- •10.10. Разложение многочлена на простые множители
- •11. Поле рациональных функций
- •11.1. Построение поля отношений.
- •11.2. Поле рациональных функций.
- •12. Прямые суммы подпространств
- •13.1. Линейное отображение и его матрица.
- •13.2. Матрица композиции линейных отображений.
- •13.3. Сумма линейных отображений и её матрица.
- •13.4. Умножение линейного отображения на элемент
- •13.5. Изоморфизм алгебры линейных операторов и
- •14. Матрица перехода от одного базиса к другому
- •14.1. Изменение координат вектора при изменении
- •14.2. Изменение матрицы линейного отображения
- •14.3. Эквивалентные матрицы.
- •15. Образ и ядро линейного отображения Пусть : l l - линейное отображение.
- •16. Инвариантные подпространства
- •16.1. Свойства инвариантных подпространств.
- •16.2. Прямая сумма инвариантных подпространств.
- •16.3. Прямая сумма линейных операторов.
- •16.4. Собственные векторы и собственные значения
- •16.6. Минимальный многочлен линейного оператора и матрицы.
- •16.7. Инвариантные подпространства линейных операторов, действующих в векторных пространствах над r и над с.
- •17. Диагонализируемые линейные операторы
- •18. Евклидовы векторные пространства
- •18.1. Определения, примеры.
- •18.2. Свойства евклидовых пространств.
- •19. Ортогональные линейные операторы
- •19.1. Определение. Свойства.
- •19.2. Ортогональная группа.
- •19.3. Структура ортогонального оператора.
- •20. Самосопряженные линейные операторы
- •20.1. Сопряженные линейные пространства.
- •20.2. Сопряженные линейные операторы.
- •20.3. Самосопряженные линейные операторы.
- •20.4. Структура самосопряженного оператора.
- •21. Унитарные векторные пространства
- •21.1. Определения, примеры.
- •22. Унитарные линейные операторы
- •22.1. Определение. Свойства.
- •22.2. Унитарная группа.
- •22.3. Структура унитарного оператора.
- •23. Эрмитовы линейные операторы
- •23.1. Сопряженное линейное пространство.
- •23.2. Сопряженные линейные операторы.
- •23.3. Эрмитовы линейные операторы.
- •23.4. Структура эрмитова оператора.
- •24. Билинейные и квадратичные формы
- •24.1. Определение билинейной функции. Общие свойства.
- •24.3. Изменение матрицы билинейной формы при изменении базисов. Ранг билинейной формы.
- •24.4. Определение квадратичной формы. Связь билинейных и квадратичных форм. Матрица и ранг квадратичной формы.
- •24.5. Эквивалентность билинейных форм и квадратичных форм.
- •24.6. Канонический и нормальный вид квадратичных и симметричных билинейных форм.
- •24.7. Закон инерции для квадратичных форм.
- •24.8. Критерий Сильвестра.
- •25. Квадратичные формы в евклидовом пространстве
- •25.1. Приведение формы ортогональным преобразова-
- •25.2. Приведение пары форм.
- •26. Эрмитовы формы
- •26.1. Определение и основные свойства эрмитовых форм.
- •26.2. Нормальный вид эрмитовых форм.
- •27. Эрмитовы формы в унитарном пространстве
- •27.1. Приведение эрмитовой формы унитарным преобразованием координат.
- •27.2. Приведение пары форм.
- •28.1. Теорема Лагранжа.
- •28.2. Факторгруппы.
- •28.3. Морфизмы групп.
- •28.4. Теорема о разложении морфизма.
- •28.5. Циклические группы.
5.9. Решение слу по Крамеру.
Рассмотрим систему п линейных уравнений с п неизвестными:
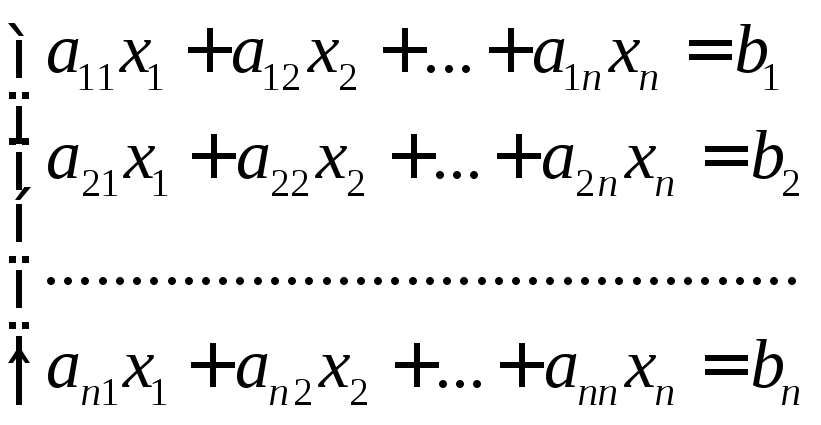 (5.1)
(5.1)
Домножим левые и правые части уравнений на алгебраические дополнения Аik основной матрицы А системы (5.1):
1-е уравнение
домножим на А1k,
второе – на А2k,
и т.д., п-е
– на Апk.
Затем домноженные уравнения сложим. У
полученного уравнения коэффициент при
хk
будет
равен
![]() =
|A|.
А коэффициент
при хs
, s
k,
равен
=
|A|.
А коэффициент
при хs
, s
k,
равен
![]() - это определитель, у которого k-й
столбец в матрице А
заменен на
s-й
столбец, то есть это определитель с
двумя одинаковыми столбцами – k-м
и s-м,
и, значит, этот определитель равен нулю.
Таким образом, коэффициенты при всех
хs
, s
k,
равны нулю. А правая часть полученного
уравнения имеет вид
- это определитель, у которого k-й
столбец в матрице А
заменен на
s-й
столбец, то есть это определитель с
двумя одинаковыми столбцами – k-м
и s-м,
и, значит, этот определитель равен нулю.
Таким образом, коэффициенты при всех
хs
, s
k,
равны нулю. А правая часть полученного
уравнения имеет вид
![]() - это определитель матрицы, которая
получается из матрицы А
заменой k-го
столбца на столбец из правых частей
системы (5.1). Этот определитель мы
будем обозначать k
=
- это определитель матрицы, которая
получается из матрицы А
заменой k-го
столбца на столбец из правых частей
системы (5.1). Этот определитель мы
будем обозначать k
=![]() .
Следовательно, после сложения домноженных
уравнений мы получим уравнение вида
|A|
хk=
k
. Это уравнение
– следствие системы (5.1).
.
Следовательно, после сложения домноженных
уравнений мы получим уравнение вида
|A|
хk=
k
. Это уравнение
– следствие системы (5.1).
Если |A|= 0 и k 0, то уравнение |A| хk= k не имеет решений, и, следовательно, система (5.1) несовместна.
Если |A| 0, то из решения по Гауссу система (5.1) - совместная и определенная, и её решения являются решениями уравнений |A| хk= k , которые имеют единственное решение хk = k / |A|. Следовательно, набор хk = k / |A|, k = 1,…,п, является единственным решением системы (5.1). Это решение и называется решением по Крамеру.
Если |A|= 0 и все k= 0, то по Крамеру систему решать нельзя. Можно решать её, например, по Гауссу. В этом случае система (5.1) либо имеет больше одного решения, либо несовместна.
Упражнение. Привести примеры систем с |A|= 0, которые имеют более одного решения, и систем, которые несовместны.
Лекция 10.
5.10. Теорема Лапласа.
Для любых s1
s2
…
sm
и t1
t2
…
tm
будем
обозначать через
![]() минор (определитель) матрицыА,
стоящий на
пересечении столбцов с номерами s1,
s2
,…, sm
и строк с
номерами t1,
t2
,…, tm
.
минор (определитель) матрицыА,
стоящий на
пересечении столбцов с номерами s1,
s2
,…, sm
и строк с
номерами t1,
t2
,…, tm
.
Пусть k1 k2 … kp - номера фиксированных столбцов (пп)-матрицы А, kp+1 kp+2 … kn – номера дополнительных (фиксированных) столбцов матрицы А.
Теорема Лапласа.
|A|
=
![]() ,
(5.2)
,
(5.2)
где i1 i2 … ip – (переменные) номера всевозможных строк, по которым ведется суммирование, ip+1 ip+2 … in - номера дополнительных строк.
Доказательство.
Очевидно, сумма в теореме Лапласа состоит
из
![]() слагаемых. По теореме о полном разложении
определителя минор
слагаемых. По теореме о полном разложении
определителя минор
![]() содержит р!
слагаемых, а минор
содержит р!
слагаемых, а минор
![]() содержит (п
– р)! слагаемых.
Если все эти слагаемые перемножить в
каждом из
содержит (п
– р)! слагаемых.
Если все эти слагаемые перемножить в
каждом из
![]() произведений миноров, то получим всего
произведений миноров, то получим всего![]() р!(п
– р)! = п!
слагаемых – ровно столько же, сколько
содержится в теореме о полном разложении
определителя |A|.
Кроме того, после перемножения все
полученные слагаемые – это одночлены,
множителями которых являются элементы
матрицы А,
выбранные по одному из каждого столбца
с номерами k1,
k2
,…, kp
и с номерами
kp+1,
kp+2,…,
kn
, то есть
элементы матрицы А,
выбранные по одному из всех столбцов,
и аналогично по одному из всех строк.
Это значит, что 1) среди этих одночленов
нет подобных членов, и 2) эти одночлены
в точности такие же, как одночлены,
которые получаются при разложении |A|
по теореме о полном разложении
определителя. Последнее, что осталось
проверить – это то, что все эти одночлены
в правой части равенства (5.2) имеют такие
же знаки, как и одночлены в разложении
определителя |A|,
или, как мы будем говорить – правильные
знаки.
р!(п
– р)! = п!
слагаемых – ровно столько же, сколько
содержится в теореме о полном разложении
определителя |A|.
Кроме того, после перемножения все
полученные слагаемые – это одночлены,
множителями которых являются элементы
матрицы А,
выбранные по одному из каждого столбца
с номерами k1,
k2
,…, kp
и с номерами
kp+1,
kp+2,…,
kn
, то есть
элементы матрицы А,
выбранные по одному из всех столбцов,
и аналогично по одному из всех строк.
Это значит, что 1) среди этих одночленов
нет подобных членов, и 2) эти одночлены
в точности такие же, как одночлены,
которые получаются при разложении |A|
по теореме о полном разложении
определителя. Последнее, что осталось
проверить – это то, что все эти одночлены
в правой части равенства (5.2) имеют такие
же знаки, как и одночлены в разложении
определителя |A|,
или, как мы будем говорить – правильные
знаки.
Лемма. Пусть k1=1, k2 =2,…, kp= р, и, следовательно,
kp+1=
р+1, kp+2=р+2,…,kn=п.
Запишем правую часть равенства (5.2) в
виде
![]()
![]() +
все остальные слагаемые.
Докажем, что все одночлены из
+
все остальные слагаемые.
Докажем, что все одночлены из
![]()
![]() имеют
правильные знаки.
имеют
правильные знаки.
Доказательство
леммы.
Произвольный одночлен из
![]()
![]() имеет вид
имеет вид
![]() ,
где
,
где
1= ,(1)=
(- 1)r,
2=
,(1)=
(- 1)r,
2=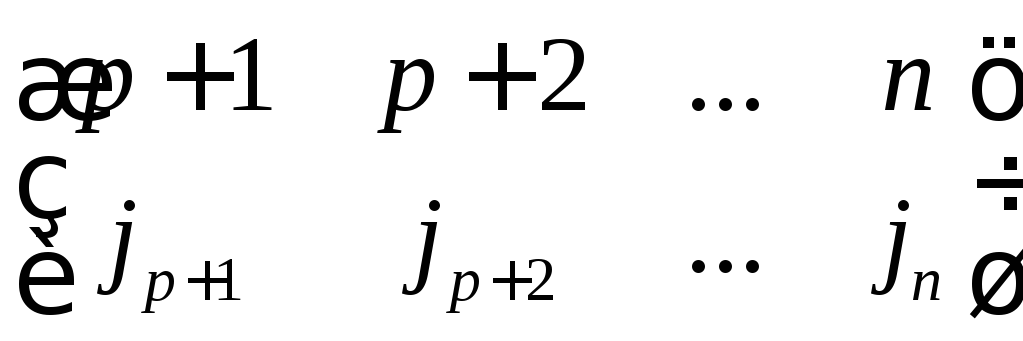 , (2)
= (- 1)s,
r
– число
инверсий подстановки 1
, s
- число
инверсий подстановки 2.
Таким образом, в правой части формулы
(5.2) одночлен
, (2)
= (- 1)s,
r
– число
инверсий подстановки 1
, s
- число
инверсий подстановки 2.
Таким образом, в правой части формулы
(5.2) одночлен
![]() имеет знак(-
1)r+s.
А в левой части формулы (5.2) в разложении
|A|
одночлен
имеет знак(-
1)r+s.
А в левой части формулы (5.2) в разложении
|A|
одночлен
![]() имеет знак
имеет знак
()= (- 1)t, где
=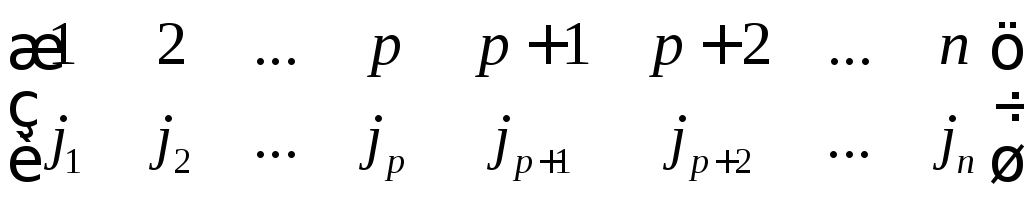 ,
а t
- число
инверсий подстановки .
Но, очевидно, t
= r
+ s,
так как у подстановки
инверсии образуют лишь элементы j1,
j2,…,
jp
между собой и элементы jр+1,
jр+2,…,
jп
между собой, а между элементами из
подмножеств j1,
j2,…,
jp
и jр+1,
jр+2,…,
jп
инверсий нет, так все элементы второго
подмножества больше элементов первого
подмножества и расположены правее.
,
а t
- число
инверсий подстановки .
Но, очевидно, t
= r
+ s,
так как у подстановки
инверсии образуют лишь элементы j1,
j2,…,
jp
между собой и элементы jр+1,
jр+2,…,
jп
между собой, а между элементами из
подмножеств j1,
j2,…,
jp
и jр+1,
jр+2,…,
jп
инверсий нет, так все элементы второго
подмножества больше элементов первого
подмножества и расположены правее.
Таким образом,
в правой части формулы (5.2) все одночлены
![]() из
из
![]()
![]() имеют правильные знаки.
имеют правильные знаки.
Лемма доказана.
Продолжим доказательство теоремы. Докажем теперь, что все одночлены в (5.2) из слагаемого
![]()
![]() имеют правильные
знаки. В матрице A
переставим k1-й
столбец на 1-е место, меняя местами его
каждый раз с соседними предыдущими
столбцами, за (k1–1)
шагов; затем
k2-й
столбец на 2-е место за (k2–2)
шагов и т.д.;
и наконец, kр-й
столбец на р-е
место за (kр–р)
шагов. После
этого столбцы с номерами kp+1,
kp+2,…,kn
займут
в матрице места с номерами р
+1, р +2,…,п .
Теперь такую же процедуру проделаем со
строками матрицы А:
строки с номерами i1,
i2,…,
ip
переставим на 1-е места за (i1
– 1)+(i2
- 2)+ +…+(
ip
– р)
шагов. После этого строки с номерами
iр+1,
iр+2,…,iп
займут места с
номерами р+1,
р +2,…,п .
Полученную матрицу обозначим А.
Её определитель
имеют правильные
знаки. В матрице A
переставим k1-й
столбец на 1-е место, меняя местами его
каждый раз с соседними предыдущими
столбцами, за (k1–1)
шагов; затем
k2-й
столбец на 2-е место за (k2–2)
шагов и т.д.;
и наконец, kр-й
столбец на р-е
место за (kр–р)
шагов. После
этого столбцы с номерами kp+1,
kp+2,…,kn
займут
в матрице места с номерами р
+1, р +2,…,п .
Теперь такую же процедуру проделаем со
строками матрицы А:
строки с номерами i1,
i2,…,
ip
переставим на 1-е места за (i1
– 1)+(i2
- 2)+ +…+(
ip
– р)
шагов. После этого строки с номерами
iр+1,
iр+2,…,iп
займут места с
номерами р+1,
р +2,…,п .
Полученную матрицу обозначим А.
Её определитель
|A|
=
![]() |A|.
По лемме все
одночлены из
|A|.
По лемме все
одночлены из
![]()
![]() для|A|
имеют
правильные знаки. Но |A|=
для|A|
имеют
правильные знаки. Но |A|=![]() |A|,
|A|,
![]() =
=
![]() ,
,
![]() =
=
![]() ,
и значит, все одночлены из
,
и значит, все одночлены из
![]()
![]() имеют правильные
имеют правильные
знаки для |A|.
Замечания.
1. Как и для разложения определителя по фиксированным р столбцам в формуле (5.2), имеет место аналогичное разложение по фиксированным р строкам, которое получается из (5.2) транспонированием.
2. Разложения определителя по произвольному столбцу (или произвольной строке) является частным случаем разложения (5.2) при р = 1.
3. Теорема об определителе с углом нулей также является частным случаем теоремы Лапласа.
Лекция 11.
ГРУППЫ, КОЛЬЦА, ПОЛЯ
