24. Билинейные и квадратичные формы

24.1. Определение билинейной функции. Общие свойства.

Определение. Билинейной функцией f на линейном пространстве L над полем P называется функция от двух векторных аргументов f: L L  P, (x, y)  f(x, y)  P, удовлетворяющая условию линейности по каждому аргументу:

1. f(x+y, z) = f(x, z)+ f(y, z) x, y, z  L, ,  P,

2. f(x, y+z) = f(x, y)+ f(x, z)  x, y, zL, ,P .

Следствия. Для билинейной функции f выполняются свойства

1. f(0_L , y) = f(x, 0_L ) = 0 x, y  L.

2.  m, n  N,

_i, _j  P, u_i, v_j L.

Упражнение. Доказать следствия.

Примеры.

1. Скалярное произведение (x,y) на евклидовом пространстве является билинейной функцей.

2. Если f₁, f₂ - линейные функции на L, то f(x, y)= f₁(х)f₂(у) – билинейная функция на L.

2. Матрица билинейной формы.

Пусть f - билинейная функция на n-мерном пространстве

L=Lⁿ над полем P, e={e₁,…,e_n} - произвольный базис в L. Для

любых x, y L имеем где все x_i ,y_j P.

Тогда

f(x, y) = f 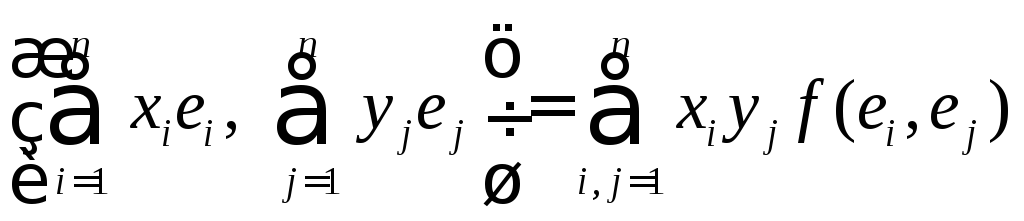. (24.1)

Формула (24.1) показывает, что функция f(x, y) является многочленом от координат х, у, все одночлены которого – первой степени по х и первой степени по у. Такой многочлен называется формой первой степени (то есть линейной) по х, и первой степени (то есть линейной) по у, то есть билинейной формой. Такие билинейные формы мы и будем изучать.

Очевидно, значение билинейной формы f(x,y) для произвольных x, y L полностью и однозначно определяется n² значениями f(e_i,e_j) на упорядоченных парах базисных векторов e_i, e_j.

Определим квадратную матрицу = (f_ij ) порядка n, где f_ij = f(e_i, e_j ), i,j = 1,…,n. Матрица называется матрицей билинейной формы f в базисе e.

Из формулы (24.1) f(x, y)== = = = .

Упражнение. Доказать обратное утверждение: если функция f задается формулой f(x, y)= , то f – билинейная функция, и матрица = (f_ij ).

24.3. Изменение матрицы билинейной формы при изменении базисов. Ранг билинейной формы.

Пусть e = {e₁,…,e_n} – ещё один базис в L, и = T =

= ( t_ij ) - матрица перехода от базиса e к базису e:

. Тогда  x, y L имеем , и

f(x ,y) = ==

= . Следовательно, из единственности матрицы билинейной формы,=.

Следствие. det = det (det T)².

Определение. Пусть f(x, y) - билинейная форма на L. Рангом билинейной формы f называется ранг ее матрицы в каком-либо базисе пространства L: rg f = rg.

Корректность определения следует из того, что ранг матрицы билинейной формы не зависит от выбора базиса: rg= rg для любых базисов e и e, так как умножение матрицы на невырожденные матрицыT ^t и T слева и справа соответственно не меняет ранга матрицы билинейной формы.

24.4. Определение квадратичной формы. Связь билинейных и квадратичных форм. Матрица и ранг квадратичной формы.

Определение. Пусть f - билинейная функция на линейном пространстве L над P. Функция F: L  P, заданная формулой F(x) = f(x, x)  x  L, называется квадратичной функцией, определяемой билинейной функцией f .

Если f(x, y)=, то F(x) = - многочлен, все одночлены которого имеют вторую степень по координатам х, то есть это форма второй степени, или же квадратичная форма. Таким образом, квадратичная функция F(x) задается квадратичной формой от координат х.

Упражнение. Доказать, что соответствие f  F не инъ-

ективно.

Определение. Билиненая форма (функция) f называется симметричной, если f(x, y) = f(y, x)  x, y  L.

Упражнение. Доказать, что f – симметрична  f(e_i, e_j) = = f(e_j, e_i)  i, j  (для некоторого) базиса e  =^t .

Утверждение. Если charP  2, то соответствие f  F между симметричными билинейными и квадратичными формами является биекцией.

Доказательство. Пусть f - симметричная билинейная форма, и f  F. Тогда  x, y L F(x + y) = f(x + y, х + у)= = f(x, х) + f(y, у) + f(x, y)+ f(y, x) = F(x) + F(y) + 2 f(x, y) 

f(x, y)=(F(x + y) - F(x) - F(y)).(24.2)

Следовательно, билинейная форма f однозначно восстанавливается по определенной ею квадратичной форме F, и значит, соответствие f  F является инъекцией.

Упражнения.

1. Пусть F – некоторая квадратичная форма (полученная, например, из билинейной не обязательно симметричной формы g). Проверить в координатах, что форма f , получен-

ная из F по формуле (24.2) будет билинейной.

2. Проверить, что эта форма f будет симметричной, и что

f  F.

Из упражнений следует, что соответствие f  F является сюръекцией и, следовательно, биекцией.



Определение. Матрицей квадратичной формы F в базисе е называется матрица соответствующей симметричной билинейной формы f : =.

Следовательно, [F] ^t = [F], и в другом базисе е

=^t. Кроме того, F(x) = ,и по определению rg F = rg f.