7.5. Теорема Кронекера-Капелли.

Запишем систему линейных уравнений (4.1) в векторном

виде 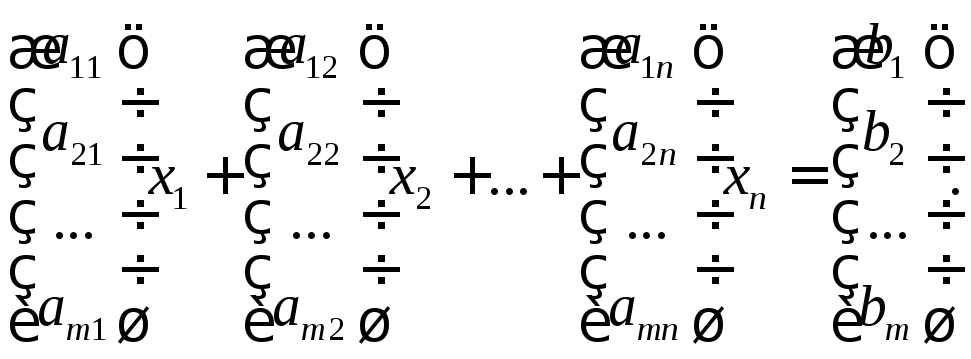ПустьАⁱ=-i-й вектор-столбец нашей системы, i = 1,…,n, B = - вектор из правой части системы. Тогда наша система может быть записана в виде одного векторного уравнения

А¹х₁ + А²х₂ +…+ А^пх_п= В. Очевидно, решение этого векторного уравнения существует тогда и только тогда, когда вектор В является линейной комбинацией векторов А¹,…,А^п  В  <А¹,…, А^п>  <В, А¹,…, А^п> <А¹,…, А^п> 

<В,А¹,…,А^п>=<А¹,…,А^п> dim<В, А¹,…,А^п>= dim<А¹,…,А^п>  rg{В,А¹,…,А^п} = rg{А¹,…,А^п}  rg A = rg - ранг основной матрицы системы (4.1) по столбцам равен рангу расширенной матрицы. Этим мы закончили ещё одно продвинутое (сравните с 4.3) доказательство теоремы Кронекера-Капелли. Далее мы увидим, что ранги матрицы по столбцам и по строкам совпадают.

7.6. Решение однородных систем линейных уравнений.

Мы рассматривали задание подпространств в L в виде линейных оболочек систем векторов. Рассмотрим второй способ задания подпространств. Пусть е = {e₁,…,е_n} – базис пространства L, ₁,…,_п фиксированные элементы из P.

Утверждение. Подмножество

L₁ = {x = x₁e₁+…+ x_nе_n  L |₁x₁ +…+_nx_n = 0} является

подпространством в L.

Доказательство. I. Пусть x = x₁e₁+…+ x_nе_n, у = у₁e₁+…+ + у_nе_n  L₁  ₁x₁ +…+_nx_n = 0, ₁у₁ +…+_nу_n = 0 

₁(x₁+у₁)+…+_n(x_п+у_п)=0, ₁x₁+…+_nx_n=0  х+у, xL₁.

II. 2. Очевидно, 0_L= 0e₁+…+ 0е_n L₁, так как ₁0 +…+_n0= 0.



Упражнение. Доказать, что не является подпространством в L подмножество {x= x₁e₁+…+x_nе_nL |₁x₁+…+_nx_n=1}.

Пусть L_i={x=x₁e₁+…+x_nе_nL|_i1x₁+…+_inx_n=0}, i =1,…,m. Тогда подпространство ∩L_i задается однородной системой линейных уравнений

. (7.1)

Это второй способ задания подпространств в L.

Пусть L=Pⁿ. Тогда множество решений системы (7.1) является подпространством в P ^п. Найдем базис и размерность этого подпространства. С помощью элементарных преобразований приведем систему (7.1) к ступенчатому виду. Для простоты будем считать, что x₁,…, x_r – главные неизвестные, а x_r+1,…, x_т – свободные неизвестные, то есть матрица системы имеет следующий ступенчатый вид:

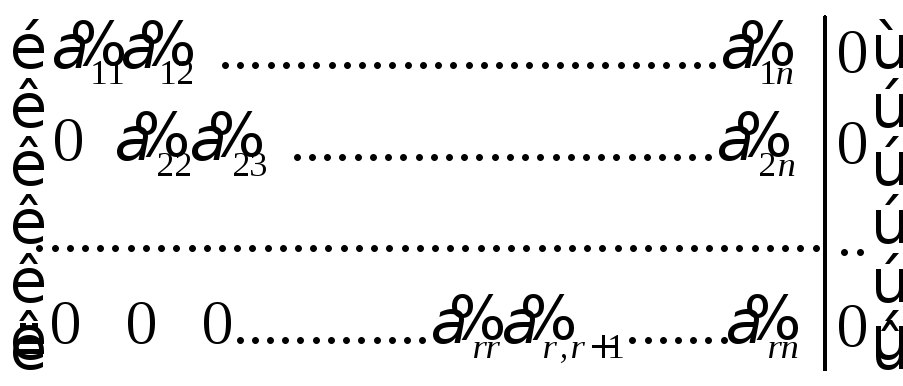. (7.2)

Будем придавать набору (п – r) свободных неизвестных значения (1,0,0,...,0,0), (0,1,0,…,0,0),…,(0,0,0,…,1,0), (0,0,0,…,0,1). После этого главные неизвестные находятся однозначно, и мы получим набор из (п – r) частных решений однородной

СЛУ f₁ = (*,*,…,*,1,0,0,...,0,0), f₂ = (*,*,…,*,0,1,0,...,0,0),…, f_n-r= (*,*,…,*,0,0,...,0,0,1), где звездочкой * обозначены какие-то значения главных неизвестных. Покажем, что f₁, f₂ ,…,f_n-r - базис в пространстве решений СЛУ (7.1). Во-первых, строки f₁, f₂,…,f_n-r – линейно независимы. Это доказывается так же, как линейная независимость строк матрицы из7.4. Во-вторых, любое решение СЛУ (7.1) является линейной комбинацией решений f₁, f₂ ,…, f_n-r . В самом деле, если решение системы f = (с₁,…,с_r+1,..., с_n), то линейная комбинация решений f₀ = f - с_r+1 f₁ - ... - с_n f_n-r принадлежит пространству решений, причем f₀ = (*,…,*,0,…,0), то есть у f₀ все свободные неизвестные равны нулю. Тогда, решая СЛУ (7.2), получим, что все главные неизвестные у f₀ также равны нулю, то есть f₀ = 0, f - с_r+1 f₁ - ...- с_n f_n-r = 0  f = с_r+1 f₁ +...+с_n f_n-r . Таким образом, f₁, f₂ ,…,f_n-r - базис в пространстве решений СЛУ (7.1), и размерность пространства решений равна (п – r).

Определение. Базис в пространстве решений однородной системы линейных уравнений называется фундаментальной системой решений (сокращенно ФСР).

Так как базисы в пространствах выбираются неоднозначно, то и ФСР выбираются неоднозначно. Мы показали, что

f₁, f₂ ,…,f_n-r – ФСР для СЛУ (7.1). Любое линейно независимое семейство из (п – r) решений также является фундаментальной системой решений.

Лекция 16.