1

2. ЦИФРОВЫЕ ФИЛЬТРЫ НА ОСНОВЕ РАЗНОСТНЫХ УРАВНЕНИЙ И ДИСКРЕТНОЙ ВРЕМЕННОЙ СВЕРТКИ

2.1.ОПРЕДЕЛЕНИЕ И КЛАССИФИКАЦИЯ ДИСКРЕТНЫХ

СИСТЕМ

Дискретной по определению называется система, осуществляющая обработку дискретных сигналов. В данном случае понятия дискретная система и дискретный сигнал используются как синонимы и математические модели цифровой системы и цифрового сигнала с

неограниченной разрядностью и точностью обработки.

Дискретная система, как и аналоговая, полностью определяется математическим оператором, устанавливающим связь между ее выходным и входным сигналами или последовательностями: y(n) = Ф[x(n)], y(t) =

Фа[x(t)]. Оператор системы, реализуемый аппаратными или программными средствами, называют алгоритмом обработки системы.

По виду оператора дискретные системы классифицируются на линейные и нелинейные, инвариантные и неинвариантные ко времени. В данном

учебном пособии рассматриваются алгоритмы цифровой фильтрации, которым соответствуют линейные дискретные системы с постоянными параметрами (или коэффициентами). Они удовлетворяют принципам суперпозиции:

y(n) = Ф[a1x1(n) + a2x2(n)] = a1Ф[x1(n)] + a2Ф[x2(n)]

(отклик системы на сумму воздействий равен сумме откликов на каждое воздействие) и инвариантности к временному сдвигу, т. е. независимости отклика от момента приложения воздействия:

y(n − m) = Ф[x(n − m)],

где x(n − m), y(n − m) − последовательности, задержанные (или сдвинутые вправо) относительно x(n) и y(n) на m отсчетов или периодов дискретизации Тд.

2

2.2. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ЛИНЕЙНЫХ ДИСКРЕТНЫХ СИСТЕМ ВО ВРЕМЕННОЙ ОБЛАСТИ

И АЛГОРИТМЫ ЦИФРОВОЙ ФИЛЬТРАЦИИ НА ИХ ОСНОВЕ

Аналоговые линейные системы во временной области математически описываются дифференциальными уравнениями и интегралом свертки [1]:

∑M	ak [ d k y( t ) / dt k ] = ∑ N bl [ d l x( t ) / dtl ],
k =	0	l=	0
(2.1)
	∞		∞
y( t ) = ∫ h(τ )x( t − τ )dτ		=	∫ x(τ )h( t − τ )dτ	(2.2)
	− ∞		− ∞

где h(t) – импульсная характеристика, являющаяся реакцией аналоговой системы на сигнал типа дельта-импульс: h( t ) = Фa [δ ( t )] .

В дискретных системах аналогом дифференциального уравнения (2.1)

является разностное уравнение:

	∑M	ak y( n − k ) =∑ N		bl x( n − l ).
	k =	0	l= 0		(2.3)
В нем, как и в	дифференциальном уравнении (2.1), M обозначает порядок
уравнения (M ≥	N), ak, bl – его весовые коэффициенты; x(n −				l), y(n − k) −
входной и выходной сигналы системы, задержанные на			l и k		отсчетов или

периодов дискретизации.

Разностное уравнение может быть получено, в частности, дискретизацией по времени дифференциального уравнения с помощью замен вида:

dx → x(n) − x(n − 1) – первая разность и т. д. [50].

При a0 = 1 разностное уравнение (2.3) приводится к виду:

y( n ) = ∑N	bl x( n − l ) −∑ M	ak y( n − k ).
l = 0	k=	1

(2.4)

Устройство или программа, реализующие разностное уравнение (2.4) (т. е. выполняющие обработку сигнала в соответствии с разностным уравнением), называются дискретным или цифровым фильтром (ЦФ).

3

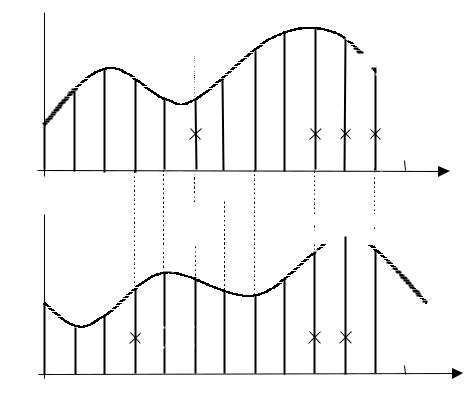
Сигнал на выходе цифрового фильтра равен сумме текущего отсчета входного сигнала x(n) и предыдущих (N и M) отсчетов входного и выходного

сигналов x(n −	l),	y(n	−	k), взвешенных (или взятых)	с весовыми
коэффициентами	bl ,	−	ak	(рис. 2.1). Достигаемое в	результате

целенаправленное изменение формы, а следовательно, и спектра сигнала отвечает общей задаче частотной фильтрации сигналов.

При значениях коэффициентов ak ≠ 0 ЦФ называется рекурсивным (РФ). Рекурсия означает наличие в фильтре обратной связи, т. е. зависимости выходного сигнала y(n) от его предыдущих отсчетов y(n − k) (рис. 2.1).

x(n)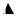

x(n-N)

bN…

n-N

y(n)

y(n-M)

aM….

n-M

x(n-2)

x(n-1)

x(n)

b2 b1 b0

n

n-2n-1 n

y(n-1) y(n-2) y(n)

a2 a1

n

n-2 n-1 n

Рис. 2.1. Графическая иллюстрация обработки сигнала в соответствии с разностным уравнением

Разностному уравнению (2.4) с коэффициентами ak = 0 соответствует

нерекурсивный фильтр (НФ):

4

y( n ) = ∑N	bl x( n − l ).
l = 0
	(2.5)

Это фильтр без обратной связи, его выходной сигнал определяется взвешенной с весами bl суммой текущего и N предыдущих отсчетов входного сигнала (рис. 2.1, верхний график). Уравнение (2.5) называют также алгоритмом скользящего весового усреднения (с нормирующим или без нормирующего множителя перед знаком суммы).

Аналогом интеграла свертки (2.2) в дискретных системах является

дискретная временная свертка (ДВС). Ее выражение получают с помощью

замен: t → nТд, τ	→	mТд, dτ → 1, ∫ → ∑	, т. е. дискретизацией (2.2):
y( n ) =	∑∞	h( m )x( n − m ) = ∑ ∞	x( m )h( n − m ).	(2.6)
	m= −∞	m=	−∞

Входящая в (2.6) дискретная функция h(m) (или h(n)) называется

импульсной характеристикой дискретной системы. Она определяется как отклик дискретной системы на сигнал типа единичный импульс u0(m) = 1, m = 0 и u0(m) = 0 при m > 0: h(m) = Ф[u0(m)]. Для физически реализуемой системы h(m) = 0 при m < 0 (отклик не может опережать воздействие); поэтому ДВС обычно представляют в виде:

y( n ) = ∑∞	h( m )x( n − m ).
m= 0
	(2.7)

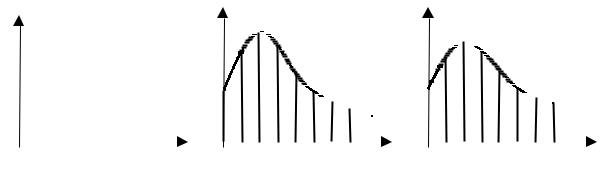
Возможны два вида импульсных характеристик ЦФ: бесконечной и конечной длительности (рис. 2.2).

5

u0(m)

h(m)

h(m)

в)

а)

б)

1

m

m

m

0 1 2 3 ……

0 1 2 3 ……

0 1 2 3 ……

N-1

Рис. 2.2. Единичный импульс (а) и импульсные характеристики цифровых фильтров БИХ-типа (б) и КИХ-типа (в)

Бесконечную импульсную характеристику имеют рекурсивные фильтры, поэтому их часто называют также БИХ-фильтрами [15]. По импульсной характеристике можно судить об устойчивости РФ. Устойчивому РФ отвечает затухающая со временем импульсная

характеристика, что математически выражается как ∑∞ | h( m )|< ∞ .

m= 0

Нерекурсивные цифровые фильтры относятся к классу КИХ-фильтров, т. е. фильтров с конечной импульсной характеристикой. Выражение ДВС

(2.7) для НФ имеет конечные пределы суммирования, определяемые длиной импульсной характеристики N:

N − 1		N − 1
y( n ) = ∑	x( m )h( n − m ) =∑	h( m )x( n − m ).
m= 0		m= 0

(2.8)

Это означает, что ДBC можно непосредственно использовать при реализации НФ в качестве алгоритма обработки, что невозможно для РФ вследствие бесконечности их импульсной характеристики и требуемого в связи с этим бесконечно большого объема вычислений.

Из сопоставления (2.5) и (2.8) следует, что значения импульсной характеристики в выражении ДВС (2.8) тождественны коэффициентам bl в разностном уравнении НФ (2.5): h(m) = bl|m=l и являются, таким образом, коэффициентами НФ. Поэтому, учитывая большое значение и

6

информативность свертки при описании дискретных сигналов и систем,

принято говорить, что НФ реализуют алгоритм цифровой фильтрации на основе ДBC (2.8), а РФ – алгоритм на основе разностного уравнения в его общей форме (2.4).

2.3. МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ СИГНАЛОВ ДИСКРЕТНЫХ СИСТЕМ НА КОМПЛЕКСНОЙ ПЛОСКОСТИ

(В ЧАСТОТНОЙ ОБЛАСТИ)

Наиболее общим для аналоговых сигналов является операторный метод их описания на комплексной плоскости:

∞	− pt dt,
X a ( p ) = ∫ x( t )e		(2.9)
0

где p = σ + jω − комплексный оператор Лапласа или комплексная частота [1]. Преобразованию Лапласа на мнимой оси jω (оси частот) соответствует

преобразование Фурье аналогового сигнала, определяющее его спектр:

∞

X a ( jω ) = X a ( p ) p= jω = ∫ x( t )e− jω t dt.

0

Для дискретных сигналов преобразование Лапласа получается из (2.9) с

помощью замен: t→	nTд , ∫ → ∑ , dt→		1, т. е. дискретизацией (2.9) по
времени:
X ( р ) =	∑∞	x( n )e− pnTд .	(2.9′)
	n= 0

Однако в отличие от аналоговых сигналов и систем преобразование (2.9′) не приводит к рациональным функциям при математическом описании дискретных сигналов и систем на комплексной Р-плоскости. Этому важнейшему условию отвечает Z-преобразование дискретных сигналов, определяемое соотношением

z = eσ Tд e

7

Z{ x( n )} = X ( z ) = ∑∞	x( n )z − n .
n= 0
(2.10)

Комплексная переменная z в (2.10) связана с переменной p (оператором Лапласа):

z = e pTд = a + jb = eσ Tд e jω Tд .

(2.11)

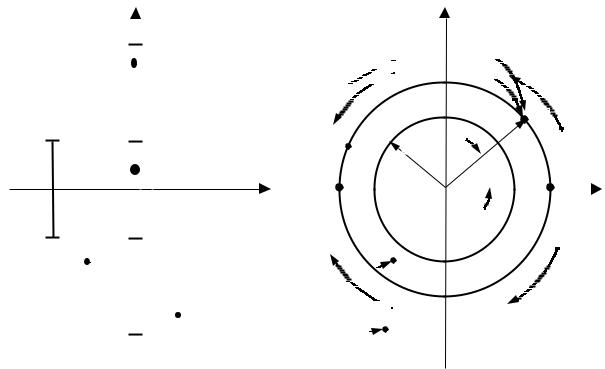
Эта связь иллюстрируется отображениями точек из комплексной P-плоскости на комплексную Z-плоскость (рис. 2.3). Особенность этих отображений заключается в их цикличности по переменной ω , обусловленой периодичностью комплексной экспоненты ejω Tд с периодом ω д:

j[ ω + kω д ]Tд , k = 0, ± 1, ± 2 и т. д.

8

Р

-

jω

Z - плоскость

jb

ПЛОСКОСТ

3ω

д/2

ω

ω д/2

e-σ 1Tд

ω 1

-σ 1

ω

1

σ

ω д/2

ω 1Tд

ω = а

0

-1

0

1

-ω

д/2

-ω д/2

-ω

-3ω д/2

Рис. 2.3. Отображения точек с комплексной Р-плоскости на Z-плоскость

Так, точки мнимой оси jω Р-плоскости (σ = 0) циклически переносятся на окружность единичного радиуса Z-плоскости; каждой полосе частот шириной ω д при этом соответствует один обход этой окружности. Однозначное отображение точек имеет место в основной полосе частот

± ω д/2. Левая P-полуплоскость (σ < 0) свертывается внутрь круга единичного радиуса Z-плоскости, а правая Р-полуплоскость (σ > 0)отображается за его пределы.

Z-преобразование, вычисленное на единичной окружности, приводит к преобразованию Фурье дискретного сигнала (1.2), определяющему его

спектр:
X ( z )| jω T		= X ( jω ) =	∑∞	x( n )e− jω nTд .	(2.12)
z= e	д		n= 0

9

Следует отметить, что Z-преобразование, как и преобразование Лапласа, может быть односторонним – для последовательностей x(n) = 0 при n < 0, так

и двусторонним, если x(n) ≠ 0	при n	< 0; в этом случае пределы
суммирования по n берутся от −	до +	[17].

К наиболее важным относятся следующие свойства Z-преобразования:

линейности:

Z{ a1 x1( n ) + a2 x2 ( n )} = a1 X1( z ) + a2 X 2 ( z )

(2.13)

(Z-преобразование суммы равно сумме Z-преобразований);

задержки:	m )} = ∑∞
Z{ x( n −		x( n −	m )z− ( n− m ) z− m = z−	m X ( z )	(2.14)
(Z-преобразование	n= 0		на m отсчетов
	задержанного			дискретного	сигнала

x(n – m) равно произведению Z-образа X(z) незадержанного сигнала х(n) на множитель задержки z-m. Этим объясняется использование символа z-m для

обозначения элемента задержки на структурных схемах систем ЦОС:
	x(n)			x(n-m)				В частности, элемент задержки на один отсчет,
		Z-m
								т. е. период дискретизации, обозначается как z-1:
					-m
	X(Z)			Z		X(Z)
						Z{ x( n − 1)} = z − 1 X ( z ));
cвертки:				y( n ) = x1( n )* x2 ( n ) = ∑∞
									x1( m )x2 ( n − m );
								m= 0
	Y( z ) =			∑∞ ∑		∞	x1( m )x2 ( n − m )z − ( n− m ) z− m = X1( z )X 2 ( z )			(2.15)
				n= 0m= 0

(Z-преобразование свертки двух последовательностей равно произведению Z- преобразований этих последовательностей);

произведения:			1		X1( v )X 2 ( v ) dv
y( n )	= x1( n )x2 ( n ); Y( z )	=		∫
(2.16)			2π	j c	v
(Z-преобразование произведения двух последовательностей равно
комплексной свертке	Z-образов этих	последовательностей, где v –

10

переменная интегрирования, С – контур интегрирования, охватывающий все особые точки подынтегральной функции).

На основе свойства (2.16) Z-преобразования произведения дискретных последовательностей доказывается важное для практики равенство Парсеваля, имеющее тот же смысл, что и для аналоговых сигналов:

∑∞	| x( nTД )|2 =			∫ X ( z )X ( z− 1 )z− 1dz =	ω	д / 2
		1	j		TД	∫ | X ( jω )|2 dω .
n= 0		2π		C	π	0

Оно означает тождественность временной и частотной оценок энергии сигнала.

Аналогичными свойствами обладает и преобразование Фурье дискретного сигнала.

Обратные Z и Фурье преобразования определяются выражениями:

Tд

ω

д / 2

)e jω

nTд dω

1

π

x( n ) =

∫

X ( jω

=

∫ X ( jλ )e jλ n dλ ,

(2.17)

2π

2π

−

ω

д

/ 2

− π

x( n ) =

1

∫ X ( z )z n− 1dz =

∑ resi [X ( z )zn− 1 ]z= z .

(2.18)

2π

j C

i

pi

Здесь обозначены:

λ = ωΤ

д =

2π f/fд

–

относительная частота, называемая

также цифровой частотой; res – вычеты подынтегральной функции F(z) = X(z)zn-1 в особых точках, охватываемых контуром С, по которому ведется интегрирование. Для дробно-рациональных функций X(z) = P(z)/Q(z) такими особыми точками являются корни полинома Q(z), называемые полюсами zpi функции X(z). Полюсы могут быть вещественными, комплексносопряженными, простыми и кратными. Вычеты в полюсах находятся с помощью выражений [17]:

для простого полюса

resi [F( z )]z= z	pi	= limz→ z	[( z − z pi )F( z )],	(2.19)
			pi

для полюса кратностью r

res	[F( z )]	=	1	lim		d r− 1	[( z −	z		)r F( z )] .	(2.20)
			( r − 1)!		z→ z pi dz r− 1
i		z= z pi							pi