14

Коэффициенты РЦФ параллельной формы реализации Количество звеньев = 5

----------------------------------------------

b0[1]=-25.009829 b1[1]=24.160216 b2[1]= 0 a1[1]=-1.7277538 a2[1]= 0.96391909 b0[2]=-17.752916 b1[2]=28.668925 b2[2]= 0 a1[2]=-1.5922191 a2[2]= 0.95609201 b0[3]= 1.6675599 b1[3]=-6.678022 b2[3]= 0 a1[3]=-1.5814839 a2[3]= 0.98708834 b0[4]= 6.6073541 b1[4]=-5.108268 b2[4]= 0 a1[4]=-1.7730814 a2[4]= 0.99029674 b0[5]= 36.197792 b1[5]=-42.57829 b2[5]= 0 a1[5]=-1.6490809 a2[5]= 0.93976056

3.3. СИНТЕЗ НЕРЕКУРСИВНЫХ ФИЛЬТРОВ МЕТОДОМ ВЕСОВЫХ ФУНКЦИЙ

3.3.1. ОСНОВЫ МЕТОДА

Синтез НФ (КИХ-фильтров) выполняется по заданной идеализированной частотной характеристике фильтра Hd(jω ) с нулевым запаздыванием и допустимым погрешностям ее аппроксимации (рис. 3.1). Он

заключается в поиске импульсной характеристики фильтра h(n)N

конечной длины N, являющейся коэффициентами его передаточной

N	− 1
функции H( z ) = ∑	h( m )z − m .
m= 0
Учитывая, что частотная характеристика и импульсная характеристика

связаны парой преобразований Фурье, с помощью обратного преобразования Фурье может быть найдена импульсная характеристика hd(n), которая соответствует заданной идеализированной частотной характеристике:

	h ( n ) =	Tд	ω	д / 2		)e jω nTд dω .
				H	( jω		(3.4)
	d	2π − ω		∫ d
				д / 2

Однако импульсная характеристика (3.4) идеального фильтра имеет

бесконечную длину и не отвечает условию физической реализуемости: при n < 0 hd(n) ≠ 0 – отклик фильтра опережает входное воздействие.

Поэтому она не может быть непосредственно использована в качестве импульсной характеристики НФ.

Например, для цифрового ФНЧ в основной полосе частот ± ω д/2.
H d ( jω ) =	1,	-ω		≤ ω ≤ ω		,
			c		c
	0,	для других			ω

Tд

ω

с

jω mT

ω сTд sinω

с mTд

λ

c

sin λ

c

m

h ( m ) =

H

( jω

)e

д dω =

=

( рис. 3.5 ).

2π

π

ω

mT

π

λ

m

d

∫ d

с

c

− ω с

д

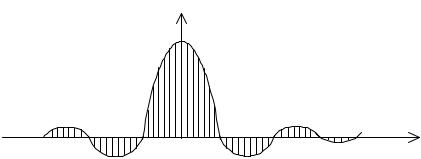
15

hd(m)

ω сТд/π

m

	2π		π	0	π	2π
−	ω сТд	−	ω сТд	ω−сТд		ω−сТд

Рис. 3.5. Импульсная характеристика идеального ФНЧ

Аналитические описания импульсных характеристик других типов ЦФ приведены в п. 3.3.6.

Получить на основе импульсной характеристики (3.4) физически реализуемый КИХ-фильтр с частотной характеристикой, близкой к заданной, можно путем сдвига hd(n) вправо на (N – 1)/2 отсчетов и усечения ее за пределами n < 0 и n ≥ N. При этом частотная характеристика фильтра аппроксимируется усеченным рядом Фурье с коэффициентами hd[n – (N –

1)/2]:

	N	− 1	− jω mTд .
H( jω	) = ∑	hd [ m − ( N − 1) / 2]e

m= 0

Известно, что простое усечение ряда Фурье сопровождается колебаниями Гиббса, возникающими при аппроксимации разрывных функций.

Для улучшения качества аппроксимации в методе весовых функций импульсную характеристику НФ конструируют ограничением длины импульсной характеристики hd[n – (N – 1)/2] с помощью специальных весовых функций или окон w(n) конечной длины N:

h( n ) = h ( n −

N − 1

)w( n ) .

(3.5)

d	2

Простое усечение эквивалентно умножению на прямоугольную весовую функцию wR(n) = 1, n = 0,..N – 1.

Полученной таким образом импульсной характеристике соответствует

	N	− 1	− jω mTд , определяемая
частотная характеристика фильтра H( jω	) = ∑	h( m )e

m= 0

сверткой в частотной области заданной частотной характеристики Hd(jω ) с частотной характеристикой (Фурье− образом) весовой функции W(jω ):

16

				ω	д / 2
	H( jω ) = W( jω ) Hd ( jω ) =		Tд		∫W( jθ )H d [ j(ω − θ )]dθ ,
			2π − ω
					д / 2
где – символ свертки, θ – переменная интегрирования,
	N	− 1
W( jω	) = ∑	w( n )e− jω nTд – частотная характеристика весовой функции.
	n=	0

Данные преобразования во временной и частотной области иллюстрируются графиками рис. 3.6, достаточно наглядно отражающими влияние весового усечения на качество аппроксимации заданной частотной характеристики усеченным рядом Фурье.

Частотная характеристика весовой функции на рис. 3.6 имеет главный лепесток шириной ∆ω гл и боковые лепестки, уровень которых характеризуется максимальным по модулю значением δ блmax и площадью под боковыми лепестками. Свертка в частотной области осуществляется графически путем смещения по частоте в пределах ± ω Д/2 зеркально отображенной частотной характеристики весовой функции и вычисления площади перекрытия ее с заданной частотной характеристикой Hd(jω ).

	|Hd(jω )|					λ c π	hd(m)
	1
− ω c	0	ω c	ω	− π λ	c		π λ	c	m
						-2 -1 0 1 2
	|W(jω	)|		w(m)			1
	δ бл.max
	∆ω гл		ω	0 1 2 3				N-1	m
H(jω )	1+δ 1max			h(m)
			δ 2 max
δ 2 max	∆ω пер		ω	0 1 2			N-1/2	N-1 m
	ω ’c	ω ’з
Рис. 3.6. Графическая иллюстрация синтеза НФ методом весовых функций

17

Из рисунка следует, что переходная полоса частотной характеристики

фильтра H(jω ) определяется шириной главного лепестка частотной характеристики весовой функции: Äùnep ≈ Äùгл , а погрешности

аппроксимации (пульсации) в полосе пропускания и задерживания δ 1, δ 2 связаны с уровнем ее боковых лепестков. Это определяет требования к весовой функции, которая должна иметь:

минимальную ширину главного лепестка ∆ω гл;

минимальный уровень боковых лепестков δ блmax и минимальную площадь под боковыми лепестками;

минимальную длину N.

Требования эти достаточно противоречивы. Так, более гладкие весовые функции имеют меньший уровень боковых лепестков, но большую ширину главного лепестка, уменьшающуюся с увеличением длины весовой функции N. Этим объясняется многообразие используемых на практике типов весовых функций. Рассмотрим параметры и математические описания некоторых из них.

3.3.2.ПАРАМЕТРЫ ВЕСОВЫХ ФУНКЦИЙ

Втабл. 3.3 приведены используемые при синтезе ЦФ параметры весовых функций прямоугольной, треугольной, Ханна, Хэмминга и Блэкмана. Кроме

значений ширины главного лепестка ∆ω гл =Dω д/N, где D − так называемый D-фактор, и максимального уровня боковых лепестков δ бл max они включают в себя также оценочные значения погрешности аппроксимации частотной характеристики в полосе задерживания (максимальные пульсации частотной характеристики) |δ 2max|, дБ, рассчитанные для цифрового ФНЧ с частотой среза λ с = π /4 [14]. Такие же погрешности имеют место и при синтезе ФВЧ. Для ЦФ с двумя и более частотами среза (ППФ, ПЗФ, МПФ) в зависимости от конкретных данных погрешность аппроксимации может быть больше ее оценочного значения, но не более чем на 6 дБ.

				Таблица 3.3.
№	Тип	∆ω гл	δ бл max, дБ	δ 2max , дБ
1	Прямоугольная	2ω д/N	− 13,6	− 21
2	Треугольная	4ω д/N	− 27	− 26
3	Ханна	4ω д/N	− 31	− 44
4	Хэмминга	4ω д/N	− 41	− 53
5	Блэкмана	6ω д/N	− 57	− 74

Руководствуясь данными табл. 3.3, можно по требуемому затуханию частотной характеристики в полосе задерживания аз сделать выбор типа весовой функции.