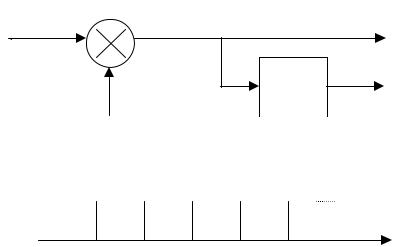
8

x(t)	xд(t)

∫

fδ (t)		x(nTд)

-2

-1

0

1

2

nTд

Рис. 1.4. Эквивалентная схема дискретизации сигнала по времени

В математике дискретные сигналы относятся к классу так называемых

решетчатых функций или временных рядов.

1.3. СПЕКТР ДИСКРЕТНОГО СИГНАЛА

Спектральную плотность дискретного сигнала X(jω ), для упрощения называемую в дальнейшем спектром, можно найти, дискретизировав по времени преобразование Фурье соответствующего ему аналогового сигнала

∞
X a ( jω ) = ∫ x( t )e− jω t dt . Заменив	t	на nТд, интеграл	на сумму и dt на Тд,
− ∞
получим	∑∞
X ( jω ) = Tд		x( nTд )e− jω nTд .	(1.2)
	n=	−∞

С другой стороны, он может быть найден и прямым преобразованием Фурье дискретного сигнала, представленного функцией непрерывного времени (1.1):

X д ( jω ) = ∫ xд ( t )e− jω t dt =	∑∞	∫ x( t )δ	( t− nTд )e− jω	t dt = ∑∞	x( nTд )e− jω nTд 1.3)
∞		∞
− ∞	n= −∞	− ∞		n=	−∞

(при выводе использовано фильтрующее свойство δ -функции [1]). Выражения (1.2) и (1.3) отличаются только масштабным (и размерным)

множителем Тд, который при односкоростной обработке обычно опускают.

д ) nTд

9

В силу периодичности комплексной экспоненты e− jω nTд = e− j(ω + kω

спектр дискретного сигнала в отличие от аналогового периодичен по частоте с периодом ω д: Х(jω ) = X[j(ω + kω д)], k = 0, ± 1, ± 2,… (рис.1.5).

Периодизация спектра обусловлена дискретизацией сигнала по времени.

Справедливо и обратное утверждение о периодичности сигналов с дискретным по частоте (или линейчатым) спектром. Оба эти свойства отвечают фундаментальному положению о взаимосвязи дискретизации и периодизации сигналов во временной и частотной области [1].

Определяют спектр дискретного сигнала в основной полосе частот

(0 ± ω д/2).

1.4. СВЯЗЬ МЕЖДУ СПЕКТРАМИ ДИСКРЕТНОГО И АНАЛОГОВОГО СИГНАЛОВ. ЯВЛЕНИЕ НАЛОЖЕНИЯ СПЕКТРОВ

Связь между спектрами дискретного и аналогового сигналов получается на основе определения дискретного сигнала (1.1), в котором дискретизирующая функция fδ (t) представляется или заменяется

аппроксимирующим ее рядом Фурье fδ ( t ) = ∑∞					Ck e jkω дt :
хд(t) = x( t ) ∑∞				k = −∞
				Ck e jkω дt .				(1.4)
			k = −∞
		1	nTд	+ Tд / 2		1	e− jkω дnTд =	1
Коэффициенты ряда Ck =				∫δ ( t − nTд )e− jkω	дt dt =				,
	Tд nT
				− T / 2		Tд		Tд
			д	д

как и следовало ожидать, соответствуют равномерному дискретному (или линейчатому) спектру этой периодической функции. Такой спектр может быть описан также непрерывным преобразованием Фурье с помощью частотной дискретизирующей функции

Fδ (jω ) =

1

∑∞

δ (ω − kω д).

Tд k =

−∞

Преобразование Фурье (1.4) при Сk =1/ Тд приводит к выражению

1

∞

∞

jkω

t

− jω

t

1

∞

Хд(jω ) =

∑

−∫∞

x( t )e

д

e

dt =

∑ X a [ j(ω − kω

д )].

(1.5)

Tд k = −∞

Tд k = −∞

Этот же результат дает свертка спектра аналогового сигнала и частотной дискретизирующей функции, соответствующая произведению (1.1) во временной области:

10

Хд(jω ) =

1

∞

X a (jϑ ) Fδ [j(ω −ϑ )]dϑ =

1

∑∞

∞

X a (jϑ )δ (ω − kω д− ϑ )dϑ =

2π −

∫∞

− ∫∞

Tд k = −∞

=

1

∑∞

X a [j(ω − kω д)].

T

−∞

д k =

Из (1.5) следует, что спектр дискретного сигнала с точностью до

постоянного множителя равен сумме спектров аналогового сигнала

Ха(jω ), смещенных по частоте на kω д. Перенос спектра Ха(jω ) на частоты kω д вызван умножением аналогового сигнала на множество комплексных

экспонент e jkω дt , являющихся гармониками дискретизирующей функции fδ (t) (см. (1.4) и рис. 1.4). Он физически объясняет явление размножения или периодизации спектров при дискретизации, которое математически обосновано в 1.3.

Выражение (1.5) может быть проиллюстрировано для различных случаев дискретизации аналоговых сигналов с ограниченным (финитным) и неограниченным спектрами, которые во временной области имеют соответственно бесконечную и конечную длительности.

Первый случай соответствует аналоговому сигналу с финитным спектром, ограниченным максимальной частотой ω m , отвечающей условию: ω m ≤ ω д/2. При этом условии (рис.1.5) спектр дискретного сигнала в основной полосе частот ± ω д/2 (при ω ≤ ω д/2) точно совпадает (до постоянного

множителя Тд) со спектром аналогового сигнала: ТдХд(jω ) = Ха(jω ).
Дискретизация не сопровождается здесь искажениями. Условие ω m ≤ ω д/2 или
ω д ≥ 2ω	m отвечает теореме отсчетов Котельникова. В этом случае возможно
точное	восстановление аналогового сигнала по его дискретным

выборкам с помощью		идеального ФНЧ с		прямоугольной частотной
характеристикой Пω	( jω	), равной Тд при ω	≤	ω д/2 и равной нулю при
	m

ω > ω д/2 (рис. 1.5).

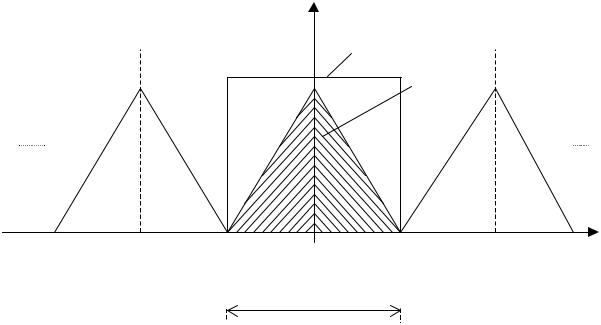
11

Tд Xд(jω )

Пω m (jω )

Xа(jω )

-ω д	-ω	m		0		ω	m	ω д	ω
	-ω	д/2				ω	д/2
				Основная	полоса

Рис. 1.5. Спектральные преобразования при дискретизации аналогового сигнала с финитным спектром в случае ω д ≥ 2ω m

Сигнал на выходе ФНЧ соответствует обратному преобразованию Фурье

	депериодизированного спектра дискретного сигнала Пω							m (jω	)Хд(jω ):
			ω	д / 2	= ∑∞		sin[ω	д ( t −	nTд ) / 2]
	x(t)=	Tд		∫ Пω m (jω ) Хд(jω ) e jω t dω		x (nTд)				. (1.6)
		2π − ω					ω д ( t − nTд ) / 2 )
				д / 2	n=−∞

Выражение (1.6) является разложением аналогового сигнала x(t) в ряд по базисным интерполирующим функциям sinx/x с весовыми коэффициентами x(nTд) (ряд Котельникова), в соответствии с которым и осуществляется его восстановление [1].

Восстановление аналогового сигнала может быть представлено также сверткой дискретного сигнала хд(t) с импульсной характеристикой идеального ФНЧ h(t), связанной обратным преобразованием Фурье с его частотной характеристикой:

			ω	д / 2
	h(t) =	Tд		∫ Пω m (jω ) e jω t dω		= (sin ω дt/2)/(ω	дt/2).	(1.7)
		2π − ω
				д	/ 2
						∞
	Подстановка (1.7) в интеграл свертки х(t) =						и его вычисление
						∫ x д(τ )h(t − τ )dτ
						− ∞

приводят к интерполяционному ряду (1.6).

12

Частота, определяемая как ω д/2 = ω m, носит известное по зарубежной литературе название частоты Найквиста.

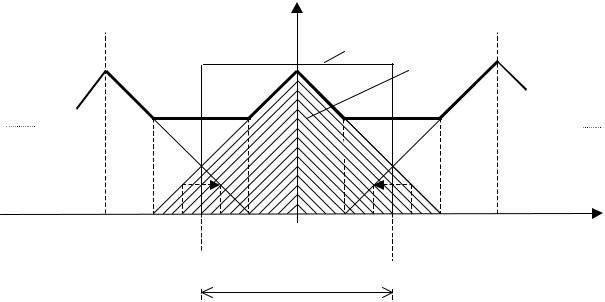
Во втором случае, когда сигнал с финитным спектром дискретизируется

с частотой ω д < 2ω m (рис.1.6,					а) спектр дискретного сигнала в основной
полосе	частот	ω	≤ ω д/2		отличается	от	спектра	аналогового
сигнала:
TдХд(jω ) ≠	Ха(jω ). Периодизация спектра Ха(jω ) здесь приводит к перекрытию
и суммированию			его	с	соседними	смещенными		по	частоте
спектрами Ха[j(ω		−	kω д)]	(на рис.1.6, а k		= ± 1). Это явление называют

наложением спектров при дискретизации. Связанные с ним погрешности дискретизации также называют погрешностями или искажениями наложения. При наложении невозможно точное восстановление аналогового сигнала по его дискретным выборкам.

					Tд Xд(jω	)
					Пω m (jω	)
						Xа(jω	)
-ω д	-ω m -ω 1	-ω′ 1		0	ω′ 1 ω 1 ω m		ω д	ω
	-ω	д/2	Основная полоса			ω д/2

Рис. 1.6 а. Спектральные преобразования при дискретизации аналогового сигнала с финитным спектром в случае ω д < 2ω m

Третий случай соответствует сигналу x(t) конечной длительности Tс с неограниченным по частоте, но затухающим спектром. Такой сигнал можно представить произведением соответствующего ему сигнала бесконечной длительности x∞ (t) и прямоугольной весовой функции ПТс(t) конечной длины Tс: x(t) = x∞ (t)ПТс(t) (так называемый временной фильтр [4]). В частотной области это соответствует свертке спектра Xa∞ (jω ) сигнала x∞ (t) с частотной

характеристикой ПТс(jω ) = sin(ω Tс/2)/(ω Tс/2) весовой функции	Xa(jω ) =
= Xa∞ (jω ) ПТс(jω ), которая и приводит к размыванию по частоте	спектра

сигнала конечной длительности. Это относится, в частности, и к простому гармоническому колебанию, спектр которого при конечной длине сигнала

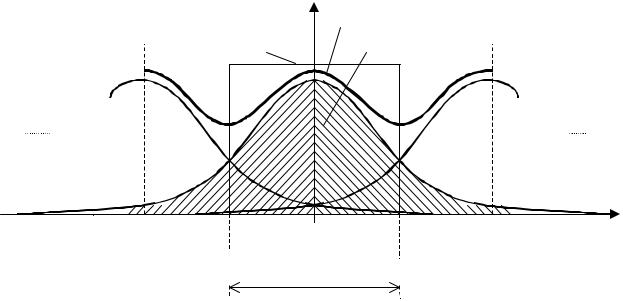
13

является теоретически бесконечным. Наложение спектров в данном случае (рис.1.6, б) имеет место при любом значении частоты дискретизации, но уровни смещенных по частоте спектров, перекрывающиеся в основной полосе, уменьшаются с ростом частоты дискретизации.

				Tд Xд(jω		)
	Пω m (jω		)	Xa(jω			)
-ω д	-ω m		0		ω m		ω д	ω
-ω	д/2	Основная полоса			ω		д/2

Рис. 1.6 б. Спектральные преобразования при дискретизации аналогового сигнала конечной длительности

Восстановленный с помощью идеального ФНЧ или интерполяционного

!	N − 1		sin[ω д ( t − nTд ) / 2	]
	∑	x (nTд)			отличается по
ряда Котельникова сигнал x(t) =			ω д ( t − nTд ) / 2 )
	n= o

форме от сигнала x(t) и имеет бесконечную длительность. Частота дискретизации сигнала конечной длительности fд = 2fm и число его отсчетов или выборок N = fдTc = 2fmTc, называемое базой сигнала x(t) [1], связываются в данном случае с некоторой частотой его спектра fm, условно принимаемой за максимальную. Она является граничной частотой финитного спектра аппроксимирующего сигнала x!(t) , совпадающего со спектром дискретного

сигнала х(nTд) в основной полосе частот ± fд/2.

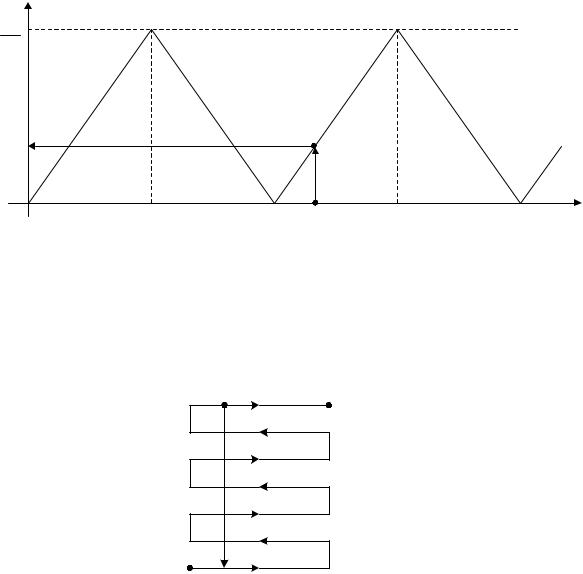
С наложением спектров при дискретизации реальных сигналов связано также явление подмены или маскирования частот, в результате которого частотный состав дискретного сигнала в основной полосе частот ± fд/2 может отличаться от состава частот аналогового сигнала в той же полосе частот. Это обусловлено тем, что высокочастотные составляющие сигнала, а также внешние шумы или помехи с частотами ω вч >ω д/2 при дискретизации трансформируются или преобразуются в основную полосу частот дискретного сигнала, создавая помехи наложения на частотах ω ’вч = |ω вч−

14

kω д| ≤ ω д/2. В общем случае такие частотные составляющие либо отсутствуют во входном сигнале, либо накладываются на существующие, искажая исходный спектр. Например, частота ω 1 на рис.1.6, а преобразуется в частоту ω ’1= ω д − ω 1. Говорят, что она подменяет частоту ω ’1 или маскируется под частоту ω ’1, которой во входном сигнале могло и не быть. График преобразования частот аналогового сигнала fАС и дискретного сигнала fДС показан на рис. 1.7.

f Д	fдс
2
f1'
					fАС
0	f Д / 2	f Д	f1	3 f Д / 2	2 f Д

Рис. 1.7. График преобразования частот при дискретизации сигнала

Другой наглядный способ анализа преобразования частот (подмены частот) [35] при дискретизации дает также диаграмма рис. 1.8.

fВЧ

3 f Д

5 f Д / 2

2 f Д

3 f Д / 2

f Д

f Д / 2

fВ'Ч

Рис. 1.8. Диаграмма подмены частот при дискретизации сигнала

Ослабить уровень помех наложения	можно, только ограничив
полосу частот дискретизируемого сигнала,	приведя ее в соответствие с

частотой дискретизации сигнала. В этом и заключается роль аналогового

15

ФНЧ на входе	системы ЦОС, как и его название −
противомаскировочный.

1.5. ОПРЕДЕЛЕНИЕ И ОЦЕНКА МЕТОДИЧЕСКОЙ ПОГРЕШНОСТИ, ВЫЗЫВАЕМОЙ ДИСКРЕТИЗАЦИЕЙ СИГНАЛА ПО ВРЕМЕНИ

Как показано выше, дискретизация сигналов с неограниченным по

частоте спектром, как и сигналов с финитным, но	не отвечающим
условию	∆ x(t) = x(t) −	x(t),
ω д ≤ ω m/2 , сопровождается методической погрешностью
	!

равной разности восстановленного и исходного аналоговых сигналов. Количественно погрешность оценивают предельным значением ∆ x(t) max

или интегральным (среднеквадратичным). Последнее определяют в виде корня квадратного из отношения энергий разностного сигнала (ошибки) Е[∆ x(t)] и исходного Е[x(t)]:

ε

= {Е[∆

x(t)]/Е[x(t)]}1/2,

∞

1

∞

2

где Е[∆ x(t)] =

∫ ∆ x2( t )dt =

∫

X a ( jω ) − X

д ( jω

)Пω д/2 ( jω )

dω ,

2π

−

∞

− ∞

∞

1

∞

2dω .

Е[x(t)] =

∫ x2( t )dt =

∫

X а( jω )

(1.8)

2π

−

∞

− ∞

Двум способам выражения энергии сигналов в (1.8) соответствуют временной и спектральный способы оценки относительной среднеквадратичной погрешности дискретизации, причем спектральный способ оценки во многих случаях оказывается эффективнее [3].

В качестве примера в соответствии с (1.8) рассчитаны погрешности дискретизации прямоугольного импульса длительностью Ти= NTд при различных значениях N = Ти/Tд = Ти fд . Результаты расчета, выполненного с

помощью программы MathCad (рис. 1.9, а) характеризуют зависимость погрешности от частоты дискретизации fд = N/Ти = N∆ fгл/2, где ∆ fгл = 2/Ти –

ширина главного лепестка спектральной плотности прямоугольного импульса. На рис. 1.9, б показан также график восстановленного сигнала x!(t) , вычисленного в моменты времени t = 0,1TД l, l = 0, 1, 2,… для случая N

=16 или fд = 16/Ти .

Опорядке погрешности дискретизации сигналов конечной длительности Tc можно судить также по соотношению [4]: ε = 1/(fmTc). При fд = 2fm и

Tc = NTд оно принимает вид: ε = 2/N. Например, при N = 100 ε = 2%.