18

3.3.3. ОПИСАНИЯ ВЕСОВЫХ ФУНКЦИЙ

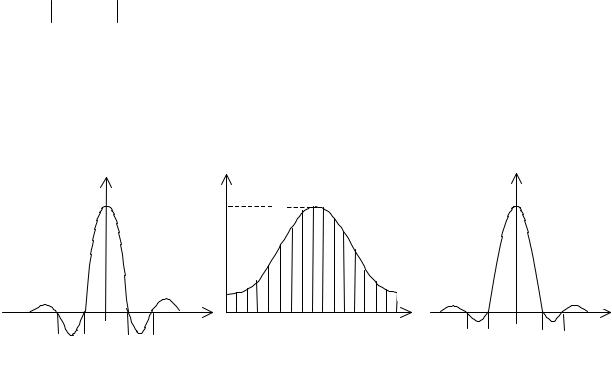
Простейшая весовая функция – прямоугольная − имеет минимальную ширину главного лепестка и максимальный уровень боковых лепестков. Частотная характеристика ее (рис. 3.7а) определяется выражением

	− jω	N −	1	Tд		sin(ω	NTд / 2 )
WR (	jω ) = e	2							.
						sin(ω	Tд / 2 )
Боковые лепестки весовой функции					имеют ширину ∆ω бл = ω д/N или

∆λ бл = 2π /N. При λ = 0 |WR(jλ )| = N.

Треугольная весовая функция является сверткой двух прямоугольных

весовых функций длиной N/2:
w T(n) = wR(n)*wR(n)={2n /( N − 1),			0 ≤ n ≤ ( N −	<	1) / 2	1)	.
2	−	2n /( N − 1),	( N − 1) / 2		n ≤ ( N −

У нее вдвое большая ширина главного лепестка при достаточно большом уровне боковых лепестков.

Частотная характеристика треугольной весовой функции равна квадрату частотной характеристики прямоугольной весовой функции половинной длины:

WT ( jω ) = sin2 (ω Tд N / 4) / sin2(ω Tд / 2) .

Боковые лепестки ее имеют ширину ∆ω бл = 2ω д/N или ∆λ бл = 4π /N. Обобщенная весовая функция Хэмминга описывается выражением

wH ( n ) = α − (1− α )cos[2π n /( N − 1)] .

При α = 0.5 она соответствует весовая функция Ханна, при α = 0.54 – весовой функции Хэмминга (рис. 3.7, б).

|WR(jλ )|	wH(n)	|WH(jλ )|
	1

			λ			n			λ
	2π 0		0 1	2		N-1		0 4π	6π
4π		2π	4π			6π	4π
− — − —		— —				− — − —		— —
N	N	N	N			N	N	N	N
	a)				б)			в)

Рис. 3.7. Частотная характеристика прямоугольной весовой функции (а),

19

весовая функция Хэмминга (б) и ее частотная характеристика (в) Уровень боковых лепестков весовой функции Хэмминга оказывается приемлемым для многих приложений НФ.

Частотную характеристику весовой функции Хэмминга (рис. 3.7, в) можно представить суммой трех частотных характеристик прямоугольных

весовых функций с центральными частотами ω 0 = 0 и ω

0 = ±ω д/N:

WH ( jω Tд ) = α WR ( jω Tд ) +

1− α

ω Tд −

2π

+

1− α

Tд +

2π

WR j

WR j

ω

.

2

2

N

N

Боковые лепестки частотной характеристики имеют ширину ∆ω

бл = ω д/N или

∆λ бл = 2π /N. Площадь под боковыми лепестками составляет 0,04 % от площади квадрата частотной характеристики весовой функции.

Весовая функция Блэкмана имеет вид

wB ( n ) = 0,42 − 0,5cos[2π n / (N − 1)] + 0,08cos[4π n / (N − 1)] .

По сравнению с весовой функцией Хэмминга у нее более широкий главный лепесток (в 1,5 раза) при очень малом уровне боковых лепестков.

Частотная характеристика весовой функции Блэкмана по сравнению с весовой функцией Хэмминга содержит два дополнительных слагаемых

0.04WR[j(ω ± 2ω д/N)]. Ширина боковых лепестков этой весовой функции

∆ω бл = ω д/N или ∆λ бл = 2π /N.

При синтезе НФ используются также эффективные весовые функции Ланцоша, Дольфа-Чебышева, Каппелини, и др. [20, 34], среди которых особое значение имеет класс весовых функций или окон Кайзера.

3.3.4.ВЕСОВЫЕ ФУНКЦИИ КАЙЗЕРА

Вотличие от других весовых функций, характеризующихся постоянными

значениями уровня боковых лепестков δ блmax и отношения D = N/(fд/∆fгл) = N/(fд/∆fпер) (D-фактор), у весовых функций Кайзера эти параметры могут широко варьироваться с помощью коэффициента β , входящего в математическое выражение этой функции:

w ( n ) =	I	0	(β	1− [2n / (N − 1)]2 )/ I	0	(β ) ,
c

где I0(x) − функция Бесселя нулевого порядка.

Благодаря этому обеспечивается наилучшее для данного метода синтеза качество аппроксимации заданной частотной характеристики или наименьший порядок фильтра при заданном качестве аппроксимации.

Кайзером путем численного интегрирования свертки составлена таблица (табл. 3.4) и получены эмпирические формулы, которые позволяют непосредственно по заданному затуханию аз = |δ 2max| (дБ) частотной

20

характеристики

H(jω ), аппроксимирующей идеальный ФНЧ,

выбрать или

рассчитать значения D-фактора и коэффициенты β

[15]:

D ≈ (аз − 7,95)/14,36 при аз>21 дБ;

D = 0,9222 при аз < 21 дБ;

0,1102 (аз − 8,7),

− 21) ,

при аз

≥

50 дБ

β =

0,5842 (а

з

−

21)0,4 + 0,07886( а

з

при 21

<

а

з

< 50 дБ .

0,

при аз

≤ 21 дБ

По вычисленному или взятому из таблицы значению D определяется необходимый порядок фильтра N ≈ Dfд/∆fпер, который округляется затем до ближайшего большего нечетного числа.

Как и для других весовых функций, в случае аппроксимации идеальных фильтров типа ППФ, ПЗФ, МПФ затухание частотной характеристики в полосе задерживания может быть меньше его табличного значения, но не более чем на 6 дБ.

				Таблица 3.4.
Aз, дБ	β	D	аз, дБ		β	D
25	1,333	1,187	65		6,204	3,973
30	2,117	1,536	70		6,755	4,321
35	2,783	1,884	75		7,306	4,669
40	3,395	2,232	80		7,857	5,017
45	3,975	2,580	85		8,408	5,366
50	4,551	2,928	90		8,959	5,714
55	5,102	3,261	95		9,501	6,062
60	5,653	3,625	100		10,061	6,410

В табл. 3.5 приведены также расчетные значения уровня пульсаций частотной характеристики в полосе пропускания, соответствующие различным значениям затухания в полосе задерживания [15].

				Таблица 3.5
аз, дБ	1 ± δ 1max, дБ	аз, дБ	1 ±	δ 1max, дБ
30	± 0.27	70	± 0.0027
40	± 0.086	80	±	0.00086
50	± 0.027	90	±	0.00027
60	± 0.0086	100	± 0.000086

3.3.5. ИМПУЛЬСНЫЕ ХАРАКТЕРИСТИКИ ИДЕАЛЬНЫХ ЦФ РАЗЛИЧНОГО ТИПА

Аналитические описания импульсных характеристик ЦФ различного типа получаются в общем случае путем выполнения обратного преобразования Фурье их идеализированных частотных характеристик ЧХ

Hd(jω ).

Для идеального цифрового ФНЧ, как показано выше, импульсная характеристика определяется выражением

21

h ( 0 ) =	λ c	;	h ( n ) =	λ c		sinλ c n	,	n = ± 1, ± 2, … .
d	π		d	π		λ c n

Импульсные характеристики ЦФ типов ФВЧ, ППФ, ПЗФ и МПФ могут быть выражены также через импульсную характеристику цифрового ФНЧ и так называемого всепропускающего фильтра ( ВПФ ). Для такого идеального фильтра сигнал на выходе совпадает с сигналом на входе:

y(n) = x (n);hd(0) = 1; hd(n) = 0 при n ≠ 0;

Hd(jω ) = 1 при |ω | ≤ ω д/2.

Частотные характеристики ФВЧ, ППФ и ПЗФ связаны с частотной характеристикой ФНЧ и ВПФ соотношениями:

H d ( jω H d ( jω H d ( jω

)ФВЧ = H d ( jω

)ППФ = H d ( jω

)ПЗФ = H d ( jω

)ВПФ −	H d ( jω	)ФНЧ ;
)ФНЧ 2	− H d ( jω	)ФНЧ1 ;
)ВПФ −	H d ( jω	)ФНЧ 2 + H d ( jω )ФНЧ1 ,

где Hd(jω )ФНЧ, Hd(jω )ФНЧ1 и Hd(jω )ФНЧ2 – частотные характеристики идеальных ФНЧ с частотами среза λ c, λ c1, λ c2, (λ c2>λ c1), соответствующими частотам среза ФВЧ, ППФ и ПЗФ. Такая же связь справедлива и для импульсных характеристик, что позволяет непосредственно записать соответствующие им аналитические выражения:

hd ( 0 )ФВЧ

hd ( 0 )ППФ

hd ( 0 )ПЗФ

=

1−

λ

c

;

h ( n ) =

−

λ c

sinλ

c n

,

n = ± 1, ±

2, .. ;

π

d

π

λ c n

=

λ

c2

−

λ

c1

;

h ( n )

=

λ

c2

sinλ

c2 n

−

λ

c1

sinλ c1n

, n = ± 1, ± 2, .. ;

π

π

d

ППФ

π

λ c2 n

π

λ c1n

=

1−

λ

c2

+

λ c1

;

h ( n )

=

λ

c1

sinλ c1n

−

λ

c2

sinλ c2 n

,

n = ± 1, ± 2, … .

π

π

d

ПЗФ

π

λ c1n

π

λ c2 n

Аналогичным образом находятся соотношения и для конкретного МПФ. К ЦФ с нестандартными частотными характеристиками относятся

цифровой дифференциатор (ЦД) и преобразователь Гильберта (ПГ).

Идеальный ЦД имеет отличную от нуля частотную характеристику

H d ( jω ) = jω

/(ω

д / 2 )

в полосе − ω с ≤ω

≤ω

с, ограниченной частотой среза ω с.

Относительно цифровых частот λ

= ω Tд частотная характеристика принимает

вид H d ( jλ ) =

jλ

/ π ,

− λ с ≤

λ

≤

λ с.

Частотной

характеристике

ЦД

1

λ

c

соответствует

импульсная

характеристика hd ( n ) =

∫

jλ

e jλ n dλ .

С

2π −

λ

π

c

помощью интегрирования по частям она приводится к следующему аналитическому выражению: