1.5. Задача квантовой механики о движении свободной частицы

Рассмотрим движение свободной частицы. Это означает, что ее потенциальная энергия.

Пусть частица движется вдоль оси . Тогдаи уравнение Шредингера для стационарных состояний будет иметь вид

. (1.5.1)

Обозначим . (1.5.2)

Здесь k- волновое число, или модуль волнового вектора. Тогда уравнение (1.5.1) будет иметь вид

. (1.5.3)

Решением уравнения (1.5.3) является функция вида

. (1.5.4)

Её можно записать также в виде

. (1.5.5)

Функция , определяемая выражениями (1.5.4) и (1.5.5) представляет собой только координатную часть волновой функции. Зависящая от времени и координат волновая функция, описывающая движение свободной частицы будет иметь вид

(1.5.6)

Уравнение (1.5.6) есть не что иное, как уравнение плоской волны в комплексной форме. Волновая функция (1.5.6) описывает плоскую монохроматическую волну де Бройля.

Проведем анализ полученного решения.

Решение уравнения Шредингера для свободной частицы существует при любых значениях энергии и волнового числа. Это означает, что Eиkмогут изменяться непрерывно.Свободная частица имеет сплошной спектр энергии.

Найдем плотность вероятности обнаружения частицы

(1.5.6)

(1.5.6)

Вероятность обнаружить свободную частицу не зависит от координат и во всех точках пространства одинакова.

1.6. Задача квантовой механики о частице в одномерной прямоугольной потенциальной яме

Рассмотрим микроскопическую частицу, движение которой ограничено вдоль оси x непроницаемыми для нее стенками при x=0 и при x=l.

Потенциальная энергия частицы может быть представлена в этом случае в следующем виде:

(1.6.1)

Граничные условия вытекают из условий непрерывности волновой функции:

и(1.6.2)

.(1.6.3)

Решение дифференциального уравнения (1.6.7) будем искать в виде

. (1.6.4)

Волновые функции должны удовлетворять граничным условиям(1.6.2) .

,

.(1.6.5)

Отсюда

.(1.6.6)

Тогда

.(1.6.7)

Условие (1.6.7)выполняется, если аргумент синуса равен

,(1.6.8)

где параметр nможет принимать целочисленные значения:n= 1,2,3…

Из условия (1.6.12) следует, что волновое числоkможет принимать только дискретные значения

.(1.6.9)

Дискретным значениям волнового числа соответствуют дискретные значения энергии

.(1.6.10)

Из выражения (1.6.14)следует, чтоэнергия частицы в потенциальной яме не может быть произвольной. Она принимает определенные дискретные значения.

Значения энергии называютсясобственными значениями. Соответствующие этим значениям волновые функции называютсясобственными функциями. Собственными функциями для частицы в потенциальной яме будут

.(1.6.11)

Коэффициент Аможет быть найден из условия нормировки волновой функции (1.3.4). Запишем это условие применительно к данной задаче

. (1.6.12)

Для интегрирования выражения (1.6.16) и нахождения коэффициентаAможно воспользоваться соотношением . Расчет приводит к следующей формуле для нормировочного множителя

. (1.6.13)

Окончательно получим

. (1.6.14)

Плотность вероятности обнаружения частицы в различных точках ямы равна

. (1.6.15)

На рис.1.4. приведены волновые функции и распределение плотности вероятности обнаружения частицы вдоль координатыxдля различныхn.

Из формулы (1.6.9) и рис.1.4 следует, чтовероятность обнаружения частицы в различных местах ямы неодинакова.Необходимо отметить, что такое поведение частицы несовместимо с представлениями о траекториях.

Используя формулу (1.6.9)и соотношение между длиной волны и волновым числом, можно рассчитать число длин волн де Бройля, укладывающихся на ширине потенциальной ямы. Получим

; .(1.6.16)

Из выражения(1.6.16)следует, что на ширине ямы укладывается целое число длин полуволн, равное значению квантового числаn (рис.1.4)

Физические величины, которые могут принимать лишь определенные дискретные значения, называют квантованными. Квантованные значения энергии называют уровнями энергии, они образуют энергетический спектр частицы.Числа n, определяющие энергетические уровни, называют квантовыми числами.

Определим энергетический интервал между двумя соседними уровнями энергии (рис.1.5). Он равен

.(1.6.17)

При достаточно больших n

.(1.6.18)

Исследуем влияние линейных размеров потенциальной ямы на квантование энергии частицы. Для этого проведем некоторые оценки. Рассмотрим движение электрона (его масса равна кг).

1. Пусть размер ямы соизмерим с размерами атома, то есть м. Тогда

Дж эВ

Сравним это значение с энергией теплового движения (величиной порядка kT), которая при комнатной температуре составляет примерно 0,025 эВ. В этом случаеE_n >> kT, и дискретность энергетических уровней будет проявляться весьма заметно.

2. Пусть размер ямы велик, то есть 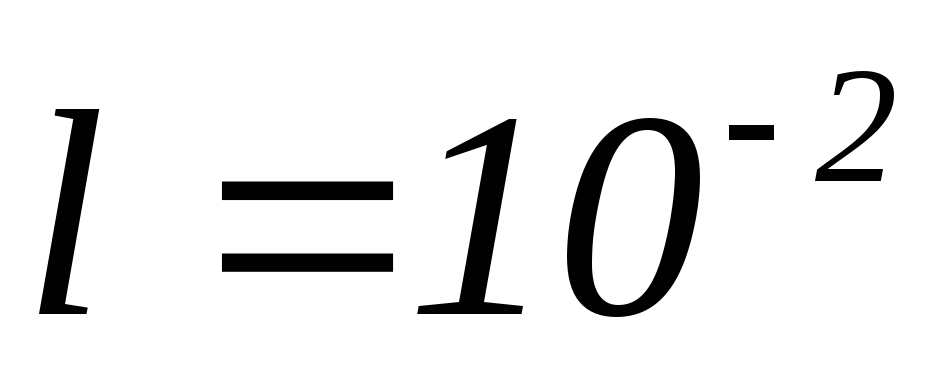м (свободные электроны в металле). Тогда

Дж эВ.

Получили E_n << kT . Энергетические уровни расположены очень густо, и энергетический спектр можно считатьквазинепрерывным.

Найдем отношение энергетического интервала между уровнями к соответствующему значению энергии . Оно будет равно

(1.6.19)

При увеличении квантового числа nотношение уменьшается. Происходит относительное сближение энергетических уровней частицы в потенциальной яме. Еслиnвелико (n>>1), то энергетический спектр можно считать квазинепрерывным.

Данный результат является частным случаем принципа соответствия Бора, согласно которому выводы и результаты квантовой механики при больших квантовых числах должны соответствовать классическим результатам.