Загальна фізика / Теоретичні курси / Коливання хвилі та оптичні явища

З врахуванням (1.55) закон руху для пружинного маятника (1.49) запишеться у виглядi

	d2x		dx
m			= −kx − r		+ F0 cos ωt.
	dt2			dt

Використовуючи (1.17) i (1.50), одержимо рiвняння

d2x			dx
		+ 2δ		+ ω02x = (F0	/m) cos ωt.	(1.56)
dt2
			dt

Якщо розглядати електричний коливальний контур, то роль X(t) вiдiграє зовнiшня е.р.с., що перiодично змiнюється за гармонiчним законом, яка пiдводиться до контуру, або змiнна напруга

U = Um cos ωt.

(1.57)

Тодi рiвняння (1.26) з врахуванням (1.57) можна записати у виглядi

d2Q			R dQ				1			Um
		+					+		Q =		cos ωt.
dt2			L dt							L
							LC

Використовуючи (1.28) i (1.51), одержимо рiвняння

d2Q		+ 2δ	dQ		+ ω02Q =	Um	cos ωt.	(1.58)
dt2			dt
						L

Коливання, що виникають пiд дiєю зовнiшньої сили або зовнiшньої е.р.с, якi перiодично змiнюються з часом, називаються вiдповiдно вимушеними механiчними i вимушеними електромагнiтними коливаннями.

Рiвняння (1.56) та (1.58) можна звести до лiнiйного неоднорiдного диференцiального рiвняння

d2s		+ 2δ	ds	+ ω2s = x		cos ωt,	(1.59)
					0
dt2			dt	0

застосовуючи згодом його розв’язок для вимушених коливань конкретної фiзичної природи (x0 у разi механiчних коливань дорiвнює F0/m, у разi електромагнiтних U/L).

Розв’язок рiвняння (1.59) дорiвнює сумi загального розв’язку (1.45) однорiдного рiвняння (1.41) i часткового розв’язку неоднорiдного рiвняння. Частковий розв’язок знайдемо в комплекснiй формi. Замiнимо праву частину рiвняння (1.59) на комплексну величину x0eiωt :

d2s		+ 2δ	ds	+ ω2s = x eiωt.		(1.60)
dt2			dt	0	0

Частковий розв’язок цього рiвняння шукатимемо у виглядi s0iηt. Пiдставляючи вираз для s i його

похiдних (	ds	= iηs0eiηt,	d2s		= −η2s0eiηt) у рiвняння (1.60), одержуємо
	dt		dt2
					s0eiηt(−η2+2iδη+ω02) = x0eiωt.	(1.61)

Оскiльки ця рiвнiсть має бути справедливою для всiх моментiв часу, то час t з нього слiд виключити. Звiдси виходить, що η = ω. Враховуючи це, з рiвняння (1.61) знайдемо величину s0 i помножимо її чисельник i знаменник на (ω02 − ω2 − 2iδω):

	s0 =	x0	= xo	(ω02 − ω2) − 2iδω	.
		(ω02 − ω2) + 2iδω		(ω02 − ω2)2 + 4δ2ω2

Це комплексне число зручно представити в експоненцiальнiй формi:

s0 = Ae−iϕ,

де

x0

A =

,

(1.62)

p(ω0

− ω

)2δω

2

2

2

+ 4δ2ω2

ϕ = arctg

.

(1.63)

(ω02 − ω2)

Отже, розв’язок рiвняння (1.60) в комплекснiй формi набуде вигля-

ду

s = Ae(iωt−ϕ).

Його дiйсна частина, що є розв’язком рiвняння (1.59), дорiвнює

s = A cos (ωt − ϕ),

(1.64)

де A i ϕ задаються вiдповiдно формулами (1.62) i (1.63).

Отже, частинний розв’язок неоднорiдного рiвняння (1.59) має вигляд

x0

2δω

Рис. 1.12.

s =

cos(ωt − arctg

).

(1.65)

q

ω02 − ω2

(ω02 − ω2)2 + 4δ2ω2

Розв’язок рiвняння (1.59) дорiвнює сумi загального розв’язку однорiдного рiвняння

s1 = A0e−δt cos(ω1t + ϕ1)

(1.66)

(див. (1.45)) i частинного розв’язку (1.65). Доданок (1.66) виконує iстотну роль тiльки на початковiй стадiї процесу (при встановленнi коливань) до тих пiр, поки амплiтуда вимушених коливань не досягне значення, яке визначається рiвнiстю (1.62).

Графiчно вимушенi коливання представленi на рис.1.12. Отже, в сталому режимi вимушенi коливання вiдбуваються на частотi ω i є гармонiчними; амплiтуда i фаза коливань, якi визначаються виразами (1.62) i (1.63), також залежать вiд ω.

Запишемо формули (1.64), (1.62) i (1.63) для електромагнiтних коливань, враховуючи, що ω2 = 1/(LC)(див. (1.28)) i δ = R/(2L)(див. (1.51)):

	Qm =					Um				;
			ωsR2 + ωL −				1		2
									(1.67)
							ωC
	tgα =				R	.
			1		− ωL
			ωC

Продиференцiювавши Q = Qm cos(ωt − α)) по t, знайдемо силу струму в контурi при сталих коливаннях:

I = −Qm sin(ωt − α) = Im cos(ωt − α + π/2),							(1.68)
де		Um
Im = ωQm =						.	(1.69)
	rR2 + (ωL − ωC )2
			1

Вираз (1.68) може бути записаний у виглядi

I = −Im cos(ωt − ϕ),

де ϕ = α − π/2 зсув за фазою мiж струмом i прикладеною напругою (див. (1.57)).

Вiдповiдно до виразу (1.67)
tgϕ= tg(α	−	π/2) =	−	1/tgα =	ωL − 1/(ωC)	.	(1.70)
					R

З формули (1.70) виходить, що струм вiдстає за фазою вiд напруги (ϕ > 0), якщо L > 1/(ωC), i випереджає напругу ( ϕ < 0), якщо L < 1/(ωC). Формули (1.69) i (1.70) можна також одержати за допомогою векторної дiаграми (див. 1.10 для змiнних струмiв).

1.9.Амплiтуда i фаза вимушених коливань (механiчних i електромагнiтних). Резонанс

Розглянемо залежнiсть амплiтуди A вимушених коливань вiд частоти ω. Механiчнi i електромагнiтнi коливання розглядатимемо одночасно, називаючи величину, що коливається, або змiщенням (x) коливного тiла з положення рiвноваги або зарядом (Q) конденсатора.

З формули (1.62) виходить, що амплiтуда заряду має максимум. Щоб визначити резонансну частоту ωрез частоту, при якiй амплiтуда A заряду досягає максимуму, потрiбно знайти максимум функцiї (1.62), або, що те ж саме, мiнiмум пiдкорiнного виразу. Продиференцiювавши пiдкорiнний вираз по ω i прирiвнявши його нулю, одержимо умову, що визначає ωрез:

−4(ω02 − ω2)ω + 8δ2ω = 0.

p

Ця рiвнiсть виконується при ω=0, ω02 − 2δ2, де тiльки позитивне значення має фiзичний змiст. Отже, резонансна частота

q

ωрез = ω02 − 2δ2. (1.71)

Явище рiзкого зростання амплiтуди вимушених коливань при наближеннi частоти змушуючої сили (частоти змушуючої змiнної напруги) до частоти, що дорiвнює або близька власнiй частотi коливальної

системи, називається резонансом (вiдповiдно механiчним або електричним). При δ2 ω02

значення ωрез, практично збiгається з власною частотою ω0 коливальної системи. Пiдставляючи (1.71) у формулу (1.62), одержимо

					x0
				Aрез =		qω02 − δ2.			(1.72)
					2δ
	На рис. 1.13 наведенi залежностi амплiтуди вимушених коливань
вiд частоги при рiзних значеннях δ. З (1.71) i (1.72) виходить: що
менше δ, то вище i правiше лежить максимум даної кривої. Якщо
ω	→	0	, то всi кривi (див.1.62)	досягають одного i того ж, вiдмiнно-
				2
го вiд нуля, граничного значення x0/ω0, яке називають статичним

вiдхиленням. У разi механiчних коливань x0 / ω02 = F0/(mω02), у разi електромагнiтних Um/(Lω2). Якщо ω → ∞, то всi кривi асимптотично прямують до нуля. Наведена сукупнiсть кривих називається

резонансними кривими.

З формули (1.72) виходить, що при малому загасаннi (δ2 ω02 )

резонансна амплiтуда змiщення (заряду)								Рис. 1.13.
Aрез =	x0	=	ω0		x0	= Q	x0	,
	2δω0				2		2
			2δ ω0				ω0

де Q добротнiсть коливальної системи (див. (1.48)), x0/ω02 розглянуте вище статичне вiдхилення. Звiдси виходить, що добротнiсть Q характеризує резонанснi властивостi коливальної системи: що бiльше Q, то бiльше Aрез.

На рис. ?? поданi резонанснi кривi для амплiтуди швидкостi (струму). Амплiтуда швидкостi (струму)

ωA =				x0ω	=				x0
	q		−			r			ω2	+ 4δ
		(ω02		ω2)2 + 4δ2ω2				(ω02	−ω2)2		2

максимальна при ω=0 i дорiвнює x0/(2δ), тобто що бiльше коефiцiєнт загасання δ, то нижчий максимум резонансної кривої. Використовуючи формули (1.17), (1.50) i (1.28), (1.51), одержимо, що амплiтуда швидкостi при механiчному резонансi дорiвнює

(Aυ)макс = x0/(2δ) = F 0/r,

а амплiтуда струму при електричному резонансi

(AI )макс = x0/(2δ) = Um/R.

З виразу tg ϕ = 2δω(ω02 − ω2) (див. (1.63)) виходить, що якщо загасання в системi вiдсутнє (δ = 0), то тiльки в цьому випадку коливання i змушуюча сила (прикладена змiнна напруга) мають однаковi фази; у всiх iнших випадках ϕ 6= 0.

Залежнiсть ϕ вiд ω при рiзних коефiцiєнтах δ графiчно подана на рис. 1.15, з якого виходить, що при змiнi ω змiнюється i зсув фаз ϕ. З формули (1.63) виходить, що при ω = 0 ϕ =0, а при ω = ω0 незалежно вiд значення коефiцiєнту загасання ϕ = π/2, тобто сила (напруга) випереджає по фазi коливання на π/2. При подальшому збiльшеннi ω зсув фаз зростає, i при ω ω0 ϕ → π, тобто фаза коливань майже протилежна фазi зовнiшньої сили (змiнної напруги). Сукупнiсть кривих, зображених на рис. 1.15, називається фазовими резонансними кривими.

Явища резонансу можуть бути як шкiдливими, так i корисними. Примiром, при конструюваннi машин та рiзного роду споруд необхiдно, щоб власна частота коливань їх не збiгалася з частотою можливих зовнiшнiх дiй, iнакше виникнуть вiбрацiї, якi можуть призвести до серйозних руйнувань. Водночас, наявнiсть резонансу дає змогу знайти навiть дуже слабкi коливання, якщо їх частота збiгається з частотою власних коливань приладу. Так, радiотехнiка, прикладна акустика, електротехнiка використовують явище резонансу.

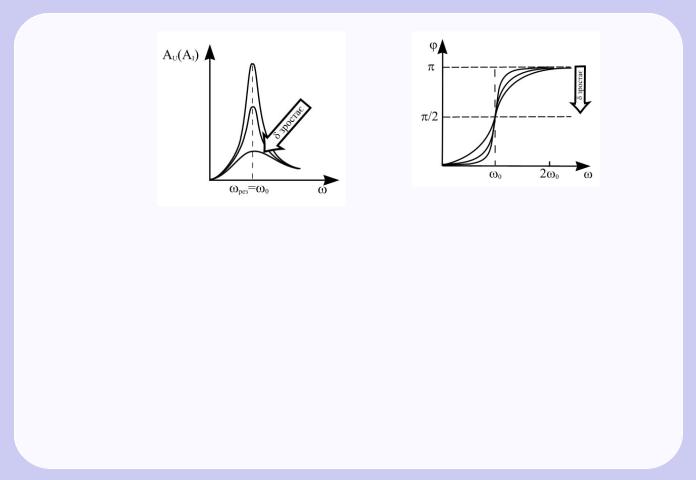
Рис. 1.14.

Рис. 1.15.

1.10.Змiнний струм

Усталенi вимушенi електромагнiтнi коливання (див. 1.8) можна розглядати як протiкання в колi, що мiстить резистор, котушку iндуктивностi i конденсатор, змiнного струму. Змiнний струм можна вважати квазiстацiонарним, тобто для нього миттєвi значення сили струму у всiх перетинах кола практично однаковi, оскiльки їх змiни вiдбуваються досить поволi, а електромагнiтнi збурення поширюються по колу з швидкiстю, що дорiвнює швидкостi свiтла. Для миттєвих значень квазiстацiонарних струмiв виконуються закон Ома i правила Кiрхгофа, якi будуть використанi стосовно змiнних струмiв (цi закони вже використовувалися при розглядi електромагнiтних коливань).

Розглянемо послiдовно процеси, якi вiдбуваються на дiлянцi кола, що мiстить резистор, котушку iндуктивностi i конденсатор, до кiнцiв якого прикладена змiнна напруга

U = Umcosωt.

(1.73)

де Um амплiтуда напруги.

1. Змiнний струм, що протiкає через резистор з опором R (L → 0, C → 0) (рис. 1.16, a). При виконаннi умови квазiстацiонарностi струм через резистор

визначається законом Ома:
I = U/R = (Um/R) cos ωt = Im cos ωt,
де амплiтуда сили струму Im = Um/R.
Для наочного зображення спiввiдношень мiж змiнними струмами
i напругами скористаємося методом векторних дiаграм. На рис. 1.16,б
показана векторна дiаграма амплiтудних значень струму Im i напруги
Um на резисторi (зсув фаз мiж Im i Um дорiвнює нулю).
2. Змiнний струм, що протiкає через котушку iндуктив-
ностi L (R → 0, C → 0) (рис. 1.17,a). Якщо в колi прикладена змiнна
напруга (1.73), то в ньому потече змiнний струм, внаслiдок чого ви-
никне е. р. с. самоiндукцiї (див. ч.2, (126.3)) Ei = −L					dI				. Тодi закон
					dt
Ома (див.ч.2, (100.3)) для даної дiлянки кола має вигляд										Рис. 1.16.
			dI
Um cos ωt − L									= 0,
				dt
звiдки
L	dI	= Um cos ωt.								(1.74)
	dt
Оскiльки зовнiшня напруга прикладена до котушки iндуктивностi, то
	UL = L		dI			,				(1.75)
			dt

є падiння напруги на котушцi. З рiвняння (1.74) виходить, що dI = (Um/L) cos ωt.

Рис. 1.17.

Рис. 1.18.