
- •Часть II
- •I.Функции нескольких переменных
- •Функция двух переменных
- •Предел функции
- •Непрерывность функции двух переменных
- •Производные и дифференциалы функции нескольких переменных
- •Частные производные высших порядков
- •Дифференцируемость и полный дифференциал функции
- •Дифференциалы высших порядков
- •Производная сложной функции. Полная производная
- •8.Инвариантность формы полного дифференциала
- •Дифференцирование неявной функции
- •Производная по направлению
- •Градиент
- •Экстремум функции двух переменных
- •Необходимые и достаточные условия экстремума
- •II. Неопределенный интеграл
- •Понятие неопределенного интеграла
- •2. Свойства неопределенного интеграла
- •3. Таблица основных неопределенных интегралов
- •4. Основные методы интегрирования
- •5. Интегрирование рациональных функций.
- •6. Интегрирование тригонометрических функций
- •7. Интегрирование иррациональных функций
- •III. Определенный интеграл
- •Определение определенного интеграла
- •Геометрический смысл определенного интеграла
- •3) Работа переменной силы
- •Формулы Ньютона-Лейбница
- •Основные свойства определенного интеграла
- •Вычисление определенного интеграла
- •Несобственные интегралы
- •7. Применение определенных интегралов для расчета геометрических и физических величин различного рода
- •7.1. Вычисление площадей плоских фигур
- •7.2 Вычисление длины дуги плоской кривой
- •7.3 Вычисление объема тела
- •8. Приближенное вычисление определенного интеграла
- •8.1. Формулы прямоугольников
- •8.2. Формула трапеций
- •8.3. Формула парабол (Симпсона)
- •IV. Кратные интегралы
- •4.1. Двойной интеграл. Основные понятия
- •4.2. Геометрический смысл двойного интеграла
- •4.3. Основные свойства двойного интеграла
- •4.4.Вычисление двойного интеграла
- •4.5. Приложения двойного интеграла
- •Статические моменты и центр тяжести плоской фигуры
- •4.6. Тройной интеграл. Основные понятия
- •4.7. Вычисление тройного интеграла.
- •4.8. Приложения тройного интеграла
- •V. Числовые ряды
- •5.1. Основные понятия
- •5.2. Необходимый признак сходимости числового ряда
- •5.3. Достаточные признаки сходимости знакопостоянных рядов
- •5.4. Признак Даламбера
- •5.5. Радикальный признак Коши
- •5.6. Интегральный признак Коши. Обобщенный гармонический ряд
- •5.7. Знакочередующиеся и знакопеременные ряды Признак Лейбница
- •5.8. Абсолютная и условная сходимость числовых рядов
- •VI.Степенные ряды
- •1 Функциональные ряды
- •1.1 Основные понятия
- •2. Некоторые приложения степенных рядов
- •2.1. Приближенное вычисление значений функций
- •2.2. Приближенное вычисление определенных интегралов
- •VII. Ряды Фурье
- •7.1. Основные понятия
- •7.2. Тригонометрический ряд Фурье
- •7.3 Разложение в ряд Фурье 2π-периодических функций. Теорема Дирихле
- •7.4. Разложение в ряд Фурье четных и нечетных функций
- •7.5. Разложение в ряд Фурье функций произвольного периода
- •VIII. Дифференциальные уравнения (д.У.)
- •8.1. Общие сведения на основании понятия о д.У.
- •8.2. Дифференциальное уравнение первого порядка
- •3. Линейные уравнения
- •Метод Бернулли
- •8.3.Дифференциальные уравнения высших порядков
- •1.Решение путем понижения порядка уравнения.
- •2.Линейные дифференциальные уравнения высших порядков.
- •8.4. Решение ду второго порядка с постоянными коэффициентами.
- •1.Решение лоду второго порядка с постоянными коэффициентами.
- •2. Решение лоду n –го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения (лнду)
- •1.Структура общего решения лнду второго порядка.
- •2.Метод вариации произвольных постоянных.
- •3.Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.
- •4.Решение лнду n- го порядка с постоянными коэффициентами и правой специальной частью.
- •Системы дифференциальных уравнений
- •Решение нормальных систем.
- •2.Системы линейных ду с постоянными коэффициентами.
4.2. Геометрический смысл двойного интеграла
Р ассмотрим
задачу по определению объема цилиндрического
тела. Пусть это тело ограничено сверху
поверхностью
ассмотрим
задачу по определению объема цилиндрического
тела. Пусть это тело ограничено сверху
поверхностью
![]() ≥0.
Снизу замкнутой областью
≥0.
Снизу замкнутой областью
![]() плоскости XOY, с боков
цилиндрической поверхностью, образующая
которой параллельна оси OZ,
а направляющей служит граница области
плоскости XOY, с боков
цилиндрической поверхностью, образующая
которой параллельна оси OZ,
а направляющей служит граница области
![]() (рис.2.).
Такое тело называется цилиндрическим.
Найдем его объем V. Для этого разобьем
область
(рис.2.).
Такое тело называется цилиндрическим.
Найдем его объем V. Для этого разобьем
область
![]() (проекция поверхности
(проекция поверхности
![]() на плоскости XOY) произвольным
образом на
на плоскости XOY) произвольным
образом на
![]() областей
областей
![]() ,
площади которых равны
,
площади которых равны
![]() .
Рассмотрим цилиндрические столбцы с
основаниями
.
Рассмотрим цилиндрические столбцы с
основаниями
![]() ,
ограниченные сверху кусками поверхности
,
ограниченные сверху кусками поверхности
![]() .
На рис.2. один из них выделен. В своей
совокупности они составляют тело
.
На рис.2. один из них выделен. В своей
совокупности они составляют тело
![]() .
Обозначив объем столбика через
.
Обозначив объем столбика через
![]() ,
получим:
,
получим:
![]() .
.
Возьмем на каждой площади
![]() произвольную точку
произвольную точку
![]() и заменим каждый столбик прямым цилиндром
с тем же основанием
и заменим каждый столбик прямым цилиндром
с тем же основанием
![]() и высотой
и высотой
![]() .
Объем этого цилиндра приближено равен
объему
.
Объем этого цилиндра приближено равен
объему
![]() цилиндрического столбика, т.е.
цилиндрического столбика, т.е.
![]() .
Тогда получим
.
Тогда получим
![]() .
Это равенство тем точнее, чем больше
число
.
Это равенство тем точнее, чем больше
число
![]() и чем меньше размеры элементарных
областей
и чем меньше размеры элементарных
областей
![]() .
Естественно принять предел этой суммы
при условии, что
.
Естественно принять предел этой суммы
при условии, что
![]() ,
а
,
а
![]() за объем
за объем
![]() цилиндрического тела, т.е.
цилиндрического тела, т.е.
![]() или записать эту сумму
или записать эту сумму
![]() .
.
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом и состоит геометрический смысл двойного интеграла.
4.3. Основные свойства двойного интеграла
С войства
двойных интегралов аналогичны свойствам
интеграла от функции одной переменной.
Поэтому мы просто ограничимся перечислением
этих свойств.
войства
двойных интегралов аналогичны свойствам
интеграла от функции одной переменной.
Поэтому мы просто ограничимся перечислением
этих свойств.
1)
![]() ,
с-const
,
с-const
2)
![]()
3) Если область
![]() разбить линией на две области D1
и D2 такие, что
разбить линией на две области D1
и D2 такие, что
![]() ,
а пересечение D1
и D2 состоит лишь из
линии их разделяющей (рис.3), то
,
а пересечение D1
и D2 состоит лишь из
линии их разделяющей (рис.3), то
![]() .
.
4) Если в области
![]() имеет место неравенство
имеет место неравенство
![]() ≥0
то и
≥0
то и
![]() .
Если в области
.
Если в области
![]() функция
функция
![]() и
и
![]() удовлетворяют неравенству
удовлетворяют неравенству
![]() ≥
≥![]() ,
то и
,
то и
![]() .
.
5)
![]() ,
так как
,
так как
![]() .
.
6) Если функция
![]() непрерывна в замкнутой области
непрерывна в замкнутой области
![]() ,
площадь которой S, то
,
площадь которой S, то
![]() ,
где
,
где
![]() и
и
![]() - соответственно D наименьшее
и наибольшее значение подинтегральной
функции в области D.
- соответственно D наименьшее
и наибольшее значение подинтегральной
функции в области D.
7) Если функция
![]() непрерывна в замкнутой области D,
площадь которой S, то в
этой области существует такая точка
непрерывна в замкнутой области D,
площадь которой S, то в
этой области существует такая точка
![]() ,
что
,
что
![]() .
Величину
.
Величину
![]() называют средним значением функции
называют средним значением функции
![]() в области
в области
![]() .
.
4.4.Вычисление двойного интеграла
Покажем, что вычисление двойного
интеграла сводится к последовательному
вычислению двух определенных интегралов.
Пусть требуется вычислить двойной
интеграл
Рис.4.![]() ,
где
,
где
![]() непрерывна в
непрерывна в
![]() .
Тогда, как это было показано выше, двойной
интеграл выражает объем цилиндрического
тела, ограниченного сверху поверхностью
.
Тогда, как это было показано выше, двойной
интеграл выражает объем цилиндрического
тела, ограниченного сверху поверхностью
![]() .
Найдем этот объем используя метод
параллельных сечений. Ранее мы п
.
Найдем этот объем используя метод
параллельных сечений. Ранее мы п оказали,
что
оказали,
что
![]() ,
где
,
где
![]() - площадь сечения плоскостью,
перпендикулярной оси ОХ, а
- площадь сечения плоскостью,
перпендикулярной оси ОХ, а
![]() ,
,
![]() - уравнения плоскостей, ограничивающих
данное тело. Положим сначала, что область
- уравнения плоскостей, ограничивающих
данное тело. Положим сначала, что область
![]() представляет собой криволинейную
трапецию, ограниченную прямыми
представляет собой криволинейную
трапецию, ограниченную прямыми
![]() и
и
![]() и кривыми
и кривыми
![]() и
и
![]() ,
причем функции
,
причем функции
![]() и
и
![]() непрерывны и таковы, что
непрерывны и таковы, что
![]() ≤
≤![]() для всех Х (Рис.4.). Такая область называется
правильной в направлении оси оу. Любая
прямая, параллельная оси OY,
пересекает границу области не более,
чем в двух точках. Построим сечение
цилиндрического тела плоскостью,
перпендикулярной оси ох.
для всех Х (Рис.4.). Такая область называется
правильной в направлении оси оу. Любая
прямая, параллельная оси OY,
пересекает границу области не более,
чем в двух точках. Построим сечение
цилиндрического тела плоскостью,
перпендикулярной оси ох.
![]() .
В сечении получим криволинейную трапецию
АВС
.
В сечении получим криволинейную трапецию
АВС![]() ,
ограниченную линиями
,
ограниченную линиями
![]() ,
где
,
где
![]() ,
Z=0,
,
Z=0,
![]() и
и
![]() (рис.5). Площадь S(x)
этой трапеции находим с помощью
определенного интеграла
(рис.5). Площадь S(x)
этой трапеции находим с помощью
определенного интеграла .
Теперь согласно методу параллельных
сечений искомый объем цилиндрического
тела может быть найден так:
.
Теперь согласно методу параллельных
сечений искомый объем цилиндрического
тела может быть найден так:
 .
С другой стороны, выше мы показали, что
объем цилиндрического тела определяется
как двойной интеграл от функции
.
С другой стороны, выше мы показали, что
объем цилиндрического тела определяется
как двойной интеграл от функции
![]() ≥0
по области
≥0
по области
![]() .
Следовательно
.
Следовательно
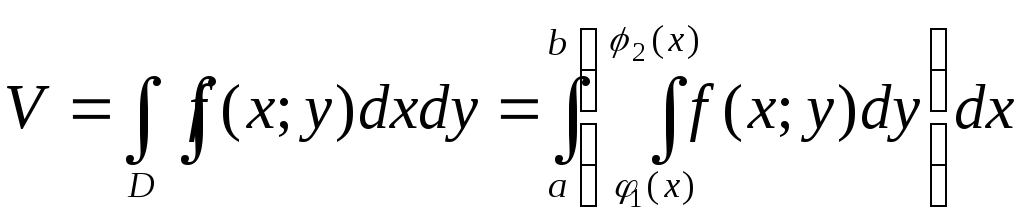 .
Это равенство обычно записывают в виде
:
.
Это равенство обычно записывают в виде
:

 .
Полученная формула представляет собой
способ вычисления двойного интеграла.
Правую часть называют двукратным или
повторным интегралом функции
.
Полученная формула представляет собой
способ вычисления двойного интеграла.
Правую часть называют двукратным или
повторным интегралом функции
![]() по области
по области
![]() .
При этом
.
При этом
 называют внутренним интегралом. Для
вычисления двукратного интеграла
сначала берем внутренний интеграл,
затем берем внешний. Т.е. результат
первого интегрирования интегрируем по
х в пределах от
называют внутренним интегралом. Для
вычисления двукратного интеграла
сначала берем внутренний интеграл,
затем берем внешний. Т.е. результат
первого интегрирования интегрируем по
х в пределах от
![]() а
до b.
а
до b.
Если же область
![]() ограничена прямыми
ограничена прямыми
![]() ,
,
![]()
![]() ,
кривыми
,
кривыми
![]() ,
,
![]() (
(![]() )
для всех у. Т.е. область
)
для всех у. Т.е. область
![]() правильна в направлении оси ох, то
рассекая тело плоскостью
правильна в направлении оси ох, то
рассекая тело плоскостью
![]() получим
получим
 .
Здесь при вычислении внутреннего
интеграла, считаем
.
Здесь при вычислении внутреннего
интеграла, считаем
![]() .
.
Пример. Вычислить
![]() ,
где
,
где
![]() ограничена линиями
ограничена линиями
![]() ,
,
![]() ,
,
![]() .
.
![]()
 ;
;
