8.4. Решение ду второго порядка с постоянными коэффициентами.
1.Решение лоду второго порядка с постоянными коэффициентами.
Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений является ЛОДУ с постоянными коэффициентами. Пусть дано ЛОДУ второго порядка.
(14)
Где p и g – const величины.
Для нахождения общего решения этого уравнения достаточно найти два его частных решения, образующих фундаментальную систему (Теорема 4).
Будем искать частные решения этого
уравнения в виде
где
k – некоторое число.
Дифференцируя эту функцию два раза и
подставляя выражения для
и
в наше уравнение получим
т.е.
или
.
Это уравнение называется характеристическим
уравнением ДУ (14).Для его составления
достаточно заменить в уравнении (14)
соответственно на
и 1.
При решении характеристического уравнения возможны следующие три случая:
-
корни
и
уравнения
действительны и различны
.
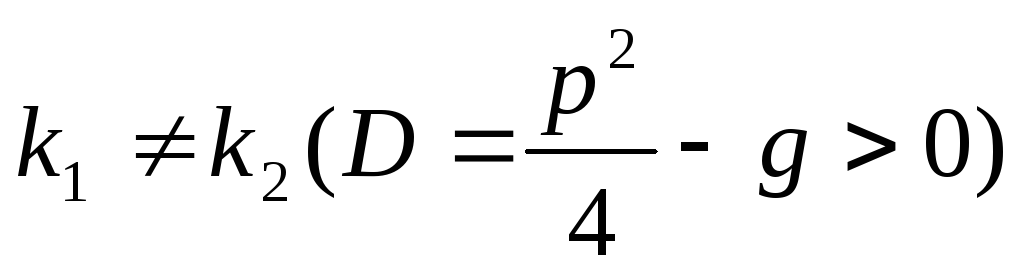В этом случае частными решениями
уравнения (14) является функция
.
Они образуют фундаментальную систему решений (линейно независимы) ,следовательно общее решение уравнения (14)в соответствии с формулой (12) имеет вид :
(15)
Пример: Решить уравнение
Составим характеристическое уравнение
,
решая его получим
.Запишем
общее решение данного уравнения
,
где
-
произвольные const.
-
корни
и
характеристического уравнения
действительные и равные
.В
этом случае имеем лишь одно частное
решение
.Кроме
того можно показать ,что наряду с
решением (14) будет и
.
Действительно, подставив
в (14)получим:
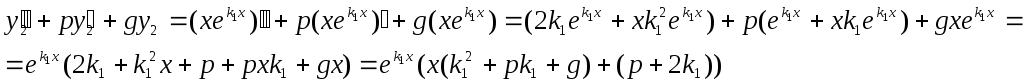
Но
т.к.
- корень этого характеристического
уравнения ,
т.к. по условию
.
Поэтому
т.е.
является решением уравнения (14).Частные
решения
и
образуют
фундаментальную систему решений
,следовательно в этом случае общее
решение ЛОДУ (14) имеет вид
(16)
-
корни
и
комплексные
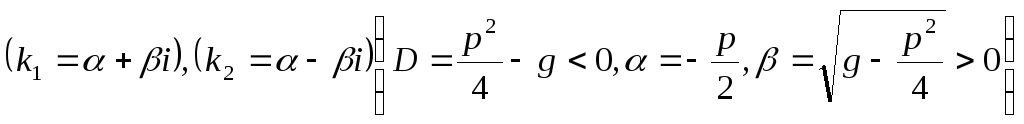В
этом случае частными решениями уравнения
(14)являются
и
.По
формуле Эйлера
тогда имеем
(14)
Найдем два действительно частных решения
уравнения, для этого составим две
линейных комбинации решений
и
.
и
Функции
и
являются решениями уравнения (14),что
следует из свойств решений ЛОДУ второго
порядка (Теорема 3).Эти решения образуют
фундаментальную систему решений, так
как они являются линейно независимыми.
Поэтому общее решение уравнения (14)
запишется в виде
(17)
Пример:
Запишем характеристическое уравнение
,
здесь
,
тогда общее решение уравнения примет
вид
Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами (14) сводится к нахождению корней характеристического уравнения и выше полученных формул для общих решений (15),(16),(17) уравнений, не прибегая к вычислению интегралов.
2. Решение лоду n –го порядка с постоянными коэффициентами.
Задача нахождения общего решения ЛОДУ
n-го порядка
с
постоянными коэффициентами
(18)
Где
- числа ,решается аналогично случаю
уравнения второго порядка с постоянными
коэффициентами.
Покажем как это делается.
Частные решения уравнения (18) будем
также искать в виде
,где
k – const.Характеристическим
для этого уравнения является алгебраическое
уравнение n-го порядка
(19)
Последнее уравнение имеет, как известно,
n корней (в их числе могут
быть и комплексные).Обозначим их через
.Кстати,
не все из корней уравнения (19) обязаны
быть различными так, например, уравнение
имеет два одинаковых корня k=2.В
этом случае говорят, что корень один
k=2 и имеет кратность
.
Если
,то
такой корень называют простым.
Вариант 1. Если все корни уравнения (19) действительны и просты, то функции
являются частными решениями уравнения
(18) и образуют фундаментальную систему
решений (линейно независимых). Поэтому
общее решение уравнения (18) запишется
в виде
Пример: Решить
Характеристическое уравнение примет
вид
и имеет корни
.Следовательно
- общее решение нашего уравнения.
Вариант 2. Все корни характеристического
уравнения действительные, но не все
простые (есть корни имеющие кратность
)
Тогда каждому простому корню k
соответствует одно частное решение
вида
,а
каждому корню k кратности
соответствует m частных
решений
.
Пример:
Характеристическое уравнение
имеет корни
, следовательно
- общее решение.
Вариант 3. Среди корней уравнения
(19) есть комплексные корни. Тогда каждой
паре
простых комплексно сопряженных корней
соответствует два частных решения
и
,а
каждой паре
корней
кратности
соответствуют 2m частных
решений вида
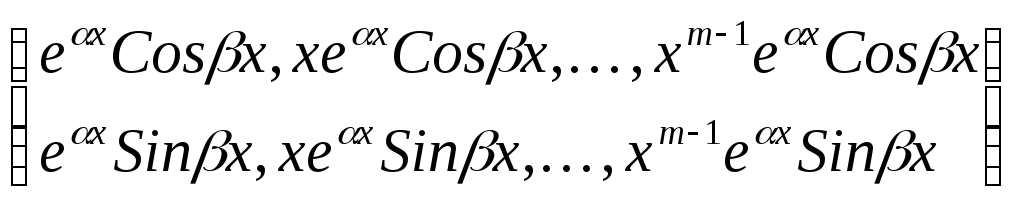
Эти решения, как можно доказать, образуют фундаментальную систему решений.
Пример:
Характеристическое уравнение
имеет корни
, следовательно
- общее решение уравнения.