1. Решение нормальных систем.

Одним из основных методов решения нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка. (Обратная задача – переход от ДУ к системе – рассмотрена ранее) Сам метод основан на следующих соображениях : Пусть задана система нормальных ДУ (1).Продифференцируем по х любое, например, первое уравнение

Подставив в это равенство значение производных из системы (1) получим

. Продолжая этот процесс (дифференцируем- подставляем- получаем ) найдем : . Соберем все уравнения в систему

(3)

Из первых (n-1) уравнений системы (3) выразим функции через , функцию и ее производные . В результате получим:

(4)

Найденные значения подставим в последнее из уравнений системы (3).Получим одно ДУ n-го порядка относительно искомой функции :

. Пусть его решение есть .

Продифференцировав его (n-1) раз и подставив значения производных в уравнения системы (4) найдем функции .

.

Пример: Решить систему уравнений

Продифференцируем первое уравнение :, подставляем в полученное равенство .

Составим систему уравнений . Из первого уравнения системы выражаем z через y и : (5)

Подставляем z во второе уравнение последней системы :

т.е.

Получили ЛОДУ второго порядка. Решаем его; характеристическое уравнение имеет вид

, - общее решение уравнения.

Найдем функцию z .Значения подставим в выражение z через (5).Получим : .

Таким образом, общее решение данной системы уравнений имеет вид:

, .

2.Системы линейных ду с постоянными коэффициентами.

Рассмотрим еще один способ решения нормальной системы уравнений (1) в случае, когда она представляет собой систему линейных однородных ДУ с постоянными коэффициентами, т .е. систему вида

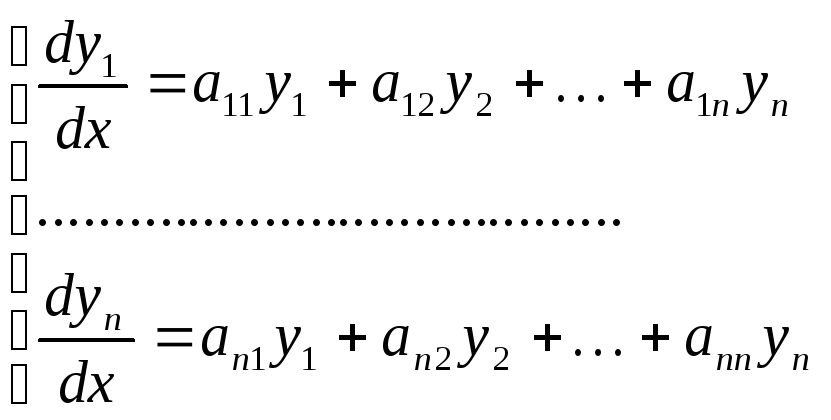
Для простоты ограничимся рассмотрением системы трех уравнений с тремя неизвестными функциями

(6)

Здесь все коэффициенты - постоянные.

Будем искать частное решение этой системы в виде

, где - постоянные, которые надо подобрать (найти) так, чтобы решение удовлетворяло нашей системе.Подставляя эти функции в систему и сокращая на множитель получим:

или (7)

Систему (7) можно рассматривать как однородную систему трех алгебраических уравнений с тремя неизвестными . Чтобы эта система имела не нулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю.

Этот определитель является характеристическим уравнением системы (6)Раскрыв определитель, получим уравнение третьей степени, относительно К. Рассмотрим все возможные случаи:

1. Корни характеристического уравнения действительны и различны : . Для каждого корня напишем систему (7)и определим коэффициенты (один из коэффициентов можно считать равным единице). Таким образом, получим:

Для корня частное решение системы (6):

Для корня

Для корня .

Можно показать, что эти функции образуют фундаментальную систему и поэтому общее решение системы (6) запишется в виде

Пример: Решить систему

Характеристическое уравнение имеет вид

или .

Частные решения системы ищем в виде

.

Найдем . При система (7) имеет вид

Последняя система имеет бесчисленное множество решений .Положив получим и получим частные решения . При система (7) имеет вид . Положив , получим .Значит корню соответствуют частные решения . Общее решение системы запишется в виде .

2. Корни характеристического уравнения различны, но среди них есть комплексные

.Вид частных решений в этой ситуации определяют также как и в 1) .

Пример: Найти частное решение системы

Составляем и решаем характеристическое уравнение

Для получим отсюда

Частное решение системы . Для получим

Отсюда находим . Частное комплексное решение системы . В полученных решениях выделим действительную и мнимую части :

Корень приведет к тем же самым решениям.

Таким образом, общее решение системы примет вид

Выделим частное решение системы. При заданных начальных условиях получим систему уравнений для определения

Следовательно, искомое решение имеет вид

3. Характеристическое уравнение имеет корень кратности .Решение системы, соответствующее кратному корню, следует искать в виде:

Это решение зависит от произвольных постоянных. Постоянные определяются методом неопределенных коэффициентов. Выразив все коэффициенты через m из них, полагаем поочередно один из них равным единице, а остальные равными нулю. Получим m линейно независимых частных решений системы (6).

Пример: Решить систему уравнений

Составим характеристическое уравнение

Корню соответствует система

Полагая, находим . Получаем первое частное решение

. Двукратному корню соответствует решение вида . Подставляя это решение в исходную систему, получим:

После сокращения на и перегруппировки

Эти равенства выполняются лишь тогда, когда

Выразим все коэффициенты через два из них (m=2) , например А и В. Из второго уравнения B=F,тогда с учетом первого уравнения получим D=B. Из четвертого уравнения находим

E=A-D, или Е=A-B. Из третьего C=E-B т.е. . Коэффициенты A и B – произвольные.

Полагая А=1,В=0, найдем : С=1,D=0, Е=1, F=0.

Полагая А=0,В=1, найдем : С=-2, D=1, E=-1, F=1.

Получим два линейно независимых частных решения, соответствующих двукратному корню .

.

И общее решение исходной системы примет вид