8.2. Дифференциальное уравнение первого порядка

Дифференциальное уравнение первого порядка в общем случае можно записать в виде:

(1)

Уравнение связывает независимую переменную х, искомую функцию у и ее производную у’, если это уравнение можно разрешить относительно у’, то его записывают в виде:

(2) и называют Д.У. первого порядка, разрешенным относительно производной. Последнее уравнение устанавливает связь между координатами точки и угловым коэффициентом у - касательной к интегральной кривой, проходящей через эту точку. Следовательно, Д.У. даст совокупность направлений (поле направлений) на плоскости ОХУ. Таково геометрическое истолкование Д.У. первого порядка.

Кривая, во всех точках которой направление поля одинаково называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить что , т.е. .

Д.У. первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме:

где и – известные функции. Последнее уравнение удобно тем, что переменные х и у в нем равноправны, т.е. любую из них можно рассматривать как функцию другой.

Интегрирование Д.У. в общем случае приводит к бесконечному множеству решений, отличающихся друг от друга на постоянные величины.

Чтобы решение Д.У. приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям. Условие, что при х=х₀ функция у должна быть равна заданному числу у₀ называется начальным условием. Начальное условие записывается в виде:

или

Общим решением Д.У. первого порядка называется функция , содержащая одну произвольную постоянную и удовлетворяющая условиям:

1. Функция является решением Д.У. при каждом фиксированном значении .

2. Каково ни было начальное условие, можно найти такое значение постоянной , что функция удовлетворяет данному начальному условию.

Частым решением Д.У. первого порядка называется любая функция , полученная из общего решения при конкретном значении постоянной .

Если общее решение Д.У. найдено в неявном виде, т.е. в виде уравнения , то такое уравнение называется общим интегралом Д.У. Уравнение в этом случае, называют частным интегралом уравнения.

С геометрической точки зрения есть семейство интегральных кривых на плоскости ХОУ, а частное решение – одна кривая из этого семейства, проходящая через точку .

Задача нахождения решения Д.У. первого порядка, удовлетворяющего заданному начальному условию, называется задачей Коши.

Теорема 8.1. Существование и единственность решения задачи Коши.

Если в уравнении (2) функция и ее частная производная непрерывны в некоторой области , содержащей точку , то существует единственное решение этого уравнения, удовлетворяющее начальным условиям.

Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая Д.У., проходящая через точку .

1. Уравнения с разделяющимися переменными

Наиболее простым Д.У. первого порядка является уравнение вида:

(3)

В этом уравнении первое слагаемое зависит от х, а второе от у. Проинтегрировав почленно это уравнение, получим:

- это общий интеграл.

Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид:

(4)

Особенности этого уравнения заключаются в том, что коэффициенты

при и представляют собой произведения двух функций, одна из которых зависит только от х, а другая от у. Уравнение (4) легко сводится к уравнению (3) путем почленного деления его на . При этом получим:

- общий интеграл.

1) При проведении почленного деления Д.У. на могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение и установить те решения Д.У., которые не могут быть получены из общего решения, так называемые – особые решения.

2) Уравнение также сводится к уравнениям, разделяющимися переменными. Для этого достаточно положить и разделить переменные.

3) Уравнение , где – числа, путем замены сводится к Д.У. с разделяющимися переменными. Дифференцируя по х, получим:

, т.е.

Откуда – интегрируя это уравнение и заменяя на , получим общий интеграл исходного уравнения.

Примеры:

1. Найти общий интеграл уравнения 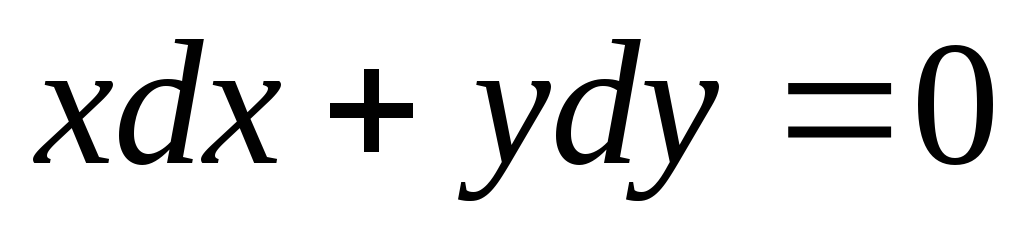. Интегрируя, получим или . Обозначив , получим – общий интеграл Д.У.

2. , преобразуем левую часть. 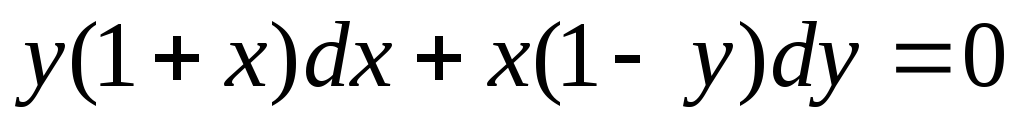. Делим на , получим . Интегрируя, получим окончательно или . Поскольку по условию решения, то решения является особыми решениями и не входят в общий интеграл.

2. Однородные дифференциальные уравнения

К уравнениям с разделяющимися переменными приводятся однородные Д.У. первого порядка.

Функция называется однородной функцией n-го порядка, если при умножении каждого ее аргумента на произвольный множитель , вся функция умножается на , т.е.

.

Например, функция есть однородная функция второго порядка, поскольку

.

Дифференциальное уравнение называется однородным, если функция есть однородная функция нулевого порядка.

Покажем, что однородное Д.У. можно записать в виде:

(4)

Если – однородная функция нулевого порядка, то по определению . Положив получим:

Однородное уравнение (4) преобразуется в уравнение с разделяющимися переменными при помощи замены переменной или, что то же самое .

Действительно, подставив и в уравнение (4), получаем или , т.е. уравнение с разделяющимися переменными. Найдя его общее решение следует заменить в нем на . Получим общее решение исходного уравнения.

Однородное уравнение часто задается в дифференциальной форме:

(5)

Это уравнение будет однородным, если и – однородные функции одинакового порядка.

Переписав (5) в виде и применив в правой части рассмотренное выше преобразование, получим уравнение . При интегрировании уравнений (5) нет необходимости предварительно приводить их к виду (4). Подстановка сразу преобразует уравнение (5) в уравнение с разделяющимися переменными.

Пример:

Найти общий интеграл уравнения.

- это однородное уравнение. Положим , тогда и получим , или после преобразований: - это уравнение с разделяющимися переменными. Делим переменные после интегрирования получим или .

Если , то , переходя к старым неизвестным, получим – решение исходного уравнения.