§6. Пучок прямых.
Пусть две несовпадающие прямые на плоскости заданы своими общими уравнениями:
l1: A1x + B1y + C1 = 0 ,
l2: A2 x + B2y + C2 = 0 .
Рассмотрим совокупность всех прямых, которые задаются различными уравнениями вида
(A1+A2) x + (B1+B2) y + C1+ C2 = 0, (20)
где и – числа не равные нулю одновременно. Это множество называется пучком прямых. Очевидно, при = 1, = 0 мы получим уравнение прямой l1, а при = 0, = 1 – уравнение прямой l2. Таким образом, прямые l1 и l2 тоже входят в пучок.
Теорема 4. 1. Если прямые l1 и l2 пересекаются в точке Mo, то определяемый ими пучок прямых, состоит из всех прямых, проходящих через Mo.
2. Если l1 l2 , то определяемый этими прямыми пучок состоит из всех параллельных им прямых.
Доказательство. 1. Перепишем (20) в виде
(A1x + B1y + C1) + (A2 x + B2 y + C2) = 0. (20)
Пусть Mo(xo, yo) = l1 l2. Тогда ее координаты удовлетворяют уравнениям обеих прямых. Подставим ее координаты в (20):
(A1xo+ B1yo+ C1) + (A2 xo+ B2 yo+ C2) = 0.
Поскольку обе скобки должны быть равны нулю, то мы получаем верное равенство независимо от и . Таким образом, все прямые пучка (20) проходят через Mo.
П
окажем,
что в пучок входят все прямые, проходящие
через Mo.
Пусть M(x1,
y1)
– произвольная точка плоскости, отличная
от Mo.
Подставим ее координаты в (20)
и обозначим
X= A1x1+ B1y1+ C1, Y = A2 x1+ B2 y1+ C2.
Получим уравнение
X + Y= 0 (*)
относительно неизвестных и . Это уравнение всегда имеет решение (o, o). При =o и =o уравнение (20) будет задавать прямую, проходящую через M.
2
.
Пусть l1
l2
. Тогда выполнено
= = k .
Пусть l – произвольная прямая из пучка (20). Применим к ней признак параллельности с прямой l2:
= + = + k + = k + ,
т.е. имеем верное равенство. Значит l l2 .
П окажем, что в пучок входят все прямые параллельные l1 и l2. Пусть M(x1, y1) – произвольная точка плоскости, не лежащая ни на l1 , ни на l2. Подставив ее координаты в (20) также получим уравнение (*) относительно неизвестных и , где X и Y оба ненулевые. При и , удовлетворяющих (*) уравнение (20) будет задавать прямую, проходящую через M.
Если все прямые пучка пересекаются в точке Mo, то точка Mo называется центром пучка, и пучок прямых называется собственным или центральным. Если все прямые пучка параллельны друг другу, то пучок называется нецентральным или несобственным.
§7. Уравнение плоскости в пространстве.
Плоскость в пространстве можно задать
а
)
с помощью точки Ao
и ненулевого
вектора n;\s\up8((
;
тогда можем
написать, что
={M
AoM;\s\up10(
–(n;\s\up8((};
(*)
б) с помощью точки Ao l и двух неколлинеарных векторов a;\s\up8(( и b;\s\up9((, параллельных ;
в) с помощью трех точек Ao, A1, A2 , не лежащих на одной прямой.
Теорема 4. 1. Плоскость , проходящая через точку Ao(xo, yo, zo), перпендикулярно вектору n;\s\up8(((A, B, C), задается в декартовой СК уравнением
A(x – xo) + B(y – yo) + C(z – zo) = 0. (21 )
2. Плоскость , проходящая через точку Ao(xo, yo, zo), параллельно двум неколлинеарным векторам a;\s\up8(( и b;\s\up9(( задается уравнением
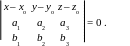
(22)
3. Плоскость , проходящая через три точки Ao(xo, yo, zo), A1(x1, y1, z1), A2(x2, y2, z2), не лежащие на одной прямой задается уравнением
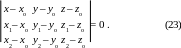
4. Плоскость , отсекающая на координатных осях ненулевые отрезки a, b, c задается уравнением
+ + = 1 (24)
(предполагается, что a, b, c могут быть отрицательными).
Доказательство. 1. Пусть M(x, y, z) – произвольная точка плоскости. Тогда AoM;\s\up10( –( n;\s\up8(( AoM;\s\up10( –( · n;\s\up8(( = 0. Поскольку AoM;\s\up10( –((x – xo, y – yo, z – zo), то последнее равенство в координатах как раз имеет вид (22).
Обратно, если координаты точки M(x, y, z) удовлетворяют (21), то AoM;\s\up10( –(n;\s\up8(( M.
2. Пусть M(x, y, z) – произвольная точка плоскости. Тогда AoM;\s\up10( –( компланарен векторам a;\s\up8(( и b;\s\up9((, а это равносильно тому, что смешанное произведение этих трех векторов равно нулю: AoM;\s\up10( –( a;\s\up8(( b;\s\up9(( = 0. В координатах последнее равенство как раз имеет вид (22).
Обратно, если координаты точки M(x, y, z) удовлетворяют (22), то векторы AoM;\s\up10( –(, a;\s\up8((, b;\s\up9(( компланарны, а значит M.
3. Если плоскость проходит через три точки Ao(xo, yo, zo), A1(x1, y1, z1), A2(x2, y2, z2), не лежащие на одной прямой, то векторы AoA1;\s\up10( –((x1– xo, y1– yo, z1– zo) и AoA2;\s\up10( –((x2 – xo, y2 – yo, z2 – zo) неколлинеарны друг другу и параллельны плоскости . Подставим их координаты в (22) вместо координат векторов a;\s\up8(( и b;\s\up9((, и получим (23).
4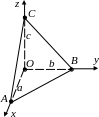
.
Условие означает, что плоскость проходит
через точки
A(a,
0,
0), B(0,
b,
0),
C(0,
0,
c).
Подставим
их координаты
в уравнение (23):
x
–
a
y
–
0
z
–
0
0 – a b – 0 0 – 0 = 0 .
0 – a 0 – 0 c – 0
Самостоятельно раскройте определитель и приведите получившееся уравнение к виду (24).
Э то уравнение называется уравнением плоскости в отрезках.
Следствие. Любая плоскость определяется уравнением вида
Ax + By + Cz + D = 0 , (25)
которое называется общим уравнением плоскости. И обратно, всякое уравнение вида (25) определяет плоскость.
Доказательство. Любая плоскость может быть задана с помощью точки и вектора нормали, а значит ее можно задать уравнением вида (21). Раскроем скобки и обозначим D = –Axo– Byo– Czo= const. Получим уравнение (25).
Обратно, пусть некоторое множество определяется уравнением (25). Пусть Ao(xo, yo, zo) – произвольная точка этого множества. Тогда ее координаты удовлетворяют (25):
Axo+ Byo+ Czo+ D = 0.
О тсюда D = –Axo– Byo– Czo , и подставляя это значение в (25) получим (21). А это уравнение, как уже известно, задает плоскость.
Рассмотрим
различные частные случаи плоскостей,
задаваемых уравнениями вида (25).
1. D = 0. Тогда уравнению
Ax + By + Cz = 0
удовлетворяют координаты точки O(0, 0, 0).
П
лоскость
проходит через начало координат.
2. C = 0. Имеем уравнение
Ax + By +D = 0.
Тогда вектор нормали к плоскости – n;\s\up8(( (A, B, 0) и n;\s\up8(( Oz, а значит, Oz.
Аналогично, при B= 0 получим Oy, а при A = 0 – Ox.
3
.
A
=
B
=
0. Имеем
уравнение
Cz + D = 0,
которое равносильно z = – C /D. Тогда
Oz.
Аналогично, при A = C = 0 будет
Oy, а при B = C = 0 – Ox.