§ A 2. Операции над векторами.

О

A₁

B₁

O₁

O

B

a;\s\up8((

b;\s\up9((a;\s\up7((

c;\s\up8((a;\s\up7((

a;\s\up8((

b;\s\up9((a;\s\up7((

?a;\s\up7((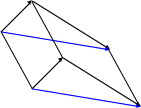

пределение. Пусть заданы два вектора a;\s\up8(( и b;\s\up9((. Отложим вектор a;\s\up8(( от произвольной точки O: a;\s\up8(( = OA;\s\up10( –(, а из точки A отложим вектор b;\s\up9((: b;\s\up9(( = AB;\s\up10( –(. Пусть c;\s\up8(( – вектор, который задается направленным отрезком OB;\s\up10( –(. Тогда c;\s\up8(( называется суммой векторов a;\s\up8(( и b;\s\up9((.

Пишем c;\s\up8(( = a;\s\up8(( + b;\s\up9((.

Этот способ построения суммы двух векторов называется правилом треугольника.

Однако, в нашем определении использо­валась произвольная точка O. Возникает вопрос: что если мы начнем построение от другой точки O₁? Не получится ли другой вектор c1;\s\up8((? Другими словами, требуется еще доказать, что наше определение корректно. Самостоятельно докажите, пользуясь чертежом, что (OA;\s\up10( –(O1A1;\s\up10( –(  AB;\s\up10( –(A1B1;\s\up10( –()  OB;\s\up10( –(O1B1;\s\up10( –(.

Свойства операции сложения векторов.

 a;\s\up8((, b;\s\up9((, c;\s\up8(( выполнено

1. a;\s\up8(( + b;\s\up9(( = b;\s\up9(( + a;\s\up8(( (коммутативность);

2. (a;\s\up8(( + b;\s\up9(( ) + c;\s\up8(( = a;\s\up8(( +( b;\s\up9(( + c;\s\up8(() (ассоциативность);

3. a;\s\up8(( + o;\s\up8(( = a;\s\up8((.

4.  x;\s\up8(( такой что a;\s\up8(( + x;\s\up8(( = o;\s\up8((. Этот вектор называется противоположным вектором к a;\s\up8(( и обозначается – a;\s\up8((.

Д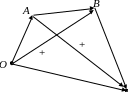 оказательство. 1. Отложим a;\s\up8(( и b;\s\up9(( от одной точки O: a;\s\up8((= OA;\s\up10( –(, b;\s\up9(( = OB;\s\up10( –(. Достроим ΔOAB до параллелограмма OACB. Пусть c;\s\up8(–( = OC;\s\up10( –(. Очевидно, что AC;\s\up10( –(OB;\s\up10( –(, т.е. b;\s\up9(( = AC;\s\up10( –(. Тогда по правилу треугольника a;\s\up8(( + b;\s\up9(( = OC;\s\up10( –(. С другой стороны, BC;\s\up10( –(OA;\s\up10( –(,  a;\s\up8(( = BC;\s\up10( –( и по правилу треугольника b;\s\up9(( + a;\s\up8(( = c;\s\up8((.

Данный способ построения суммы векторов называется правилом параллелограмма.

2

C

. Доказательство обозначено на чертеже. Здесь мы видим, что с одной стороны, (a;\s\up8(( + b;\s\up9(( ) + c;\s\up8(( = = OC;\s\up10( –(, а с другой стороны, a;\s\up8(( + (b;\s\up9(( + c;\s\up8(( ) = OC;\s\up10( –(.

Это свойство позволяет использовать обозначение a;\s\up8(( + b;\s\up9(( + c;\s\up8(( без расстановки скобок.

3. Пусть a;\s\up8((= OA;\s\up10( –(, а o;\s\up8(( можем задать с помощью направленного отрезка AA;\s\up10( –(. Тогда по правилу треугольника a;\s\up8(( + o;\s\up8(( = OA;\s\up10( –( . Значит, a;\s\up8(( + o;\s\up8(( = a;\s\up8(( .

4. Пусть a;\s\up8(( = OA;\s\up10( –( . Зададим x;\s\up8(( = AO;\s\up10( –( . Тогда по правилу треугольника a;\s\up8(( + x;\s\up8(( = OO;\s\up10( –( . Значит, a;\s\up8(( + x;\s\up8(( = o;\s\up8(( . Тем самым мы доказали существование противоположного вектора. Докажем единственность.

Предположим, что существует еще один вектор x1;\s\up8(( такой что a;\s\up8(( + x1;\s\up8(( = o;\s\up8((. Прибавим к последнему равенству справа и слева вектор x;\s\up8((:

(a;\s\up8(( + x1;\s\up8(() + x;\s\up8(( = o;\s\up8(( + x;\s\up8((.

Используя свойства 1 и 2 получаем

( a;\s\up8(( + x;\s\up8(( ) + x1;\s\up8(( = o;\s\up8(( + x;\s\up8((  o;\s\up8(( + x1;\s\up8(( = o;\s\up8(( + x;\s\up8((  x1;\s\up8(( = x;\s\up8((.

О пределение. Разностью двух векторов a;\s\up8(( и b;\s\up9(( называется такой вектор d;\s\up9((, что b;\s\up9(( + d;\s\up9(( = a;\s\up8((. Пишем d;\s\up9(( = a;\s\up8(( – b;\s\up9((.

Докажем, что разность векторов существует и определяется однозначно.

Отложим a;\s\up8(( и b;\s\up9(( от одной точки O: a;\s\up8(( = OA;\s\up10( –(, b;\s\up9(( = OB;\s\up10( –(, и пусть d;\s\up9(( = BA;\s\up10( –(. Тогда по правилу треугольника b;\s\up9(( + c;\s\up8(( = a;\s\up8(( (_*). Значит, разность двух векторов существует.

Докажем единственность. Прибавим справа и слева к к равенству (*) вектор – b;\s\up9((:

(b;\s\up9(( + d;\s\up9(( ) + (– b;\s\up9(( ) = a;\s\up8(( + (– b;\s\up9(( ).

Используя свойства 1 и 2 получаем

d;\s\up9(( + o;\s\up8(–( = a;\s\up8(( + (– b;\s\up9(( )  d;\s\up9(( = a;\s\up8(( + (– b;\s\up9(( ).

Тем самым мы доказали, что a;\s\up8(( – b;\s\up9(( = a;\s\up8(( + (– b;\s\up9(( ). А поскольку единственность противоположного вектора мы уже доказали, то и разность определяется однозначно. Кроме того, мы увидели, как построить разность на чертеже.

Определение. Произведением вектора a;\s\up8(( на число  называется такой вектор b;\s\up9((, что

1. a;\s\up8((  b;\s\up9((, если  > 0, и a;\s\up8((  b;\s\up9((, если  < 0 ;

2. ^|b;\s\up9(( ^| = ^|^|·^|a;\s\up8(( ^|.

Пишем b;\s\up9(( = a;\s\up8((. (Часто еще добавляют 3. если  = 0, то b;\s\up9(( = o;\s\up8(–(. Но это следует из 2.)

Свойства операции умножения вектора на число.

1. ( a;\s\up8(( + b;\s\up9(( ) = a;\s\up8(( + b;\s\up9((; 3. ( + )a;\s\up8(( = a;\s\up8(( + a;\s\up8((;

2. (a;\s\up8(( ) = ()a;\s\up8((; 4. 1·a;\s\up8(( = a;\s\up8((.

Д оказательство. 1. Пусть

(_**)

a;\s\up8((= OA;\s\up10( –(, b;\s\up9(( = AB;\s\up10( –(,

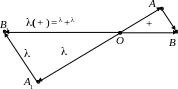
a;\s\up8((= OA1;\s\up10( –(, b;\s\up9(( = A1B1;\s\up10( –(.

Тогда по правилу треугольника

a;\s\up8(( + b;\s\up9(( = OB;\s\up10( –( , a;\s\up8(( + b;\s\up9(( = OB1;\s\up10( –(.

Нам требуется доказать, что (a;\s\up8(( + b;\s\up9(( ) = OB1;\s\up10( –(.

Из (_**) вытекает по-добие треугольников ΔOAB   ΔOA₁B₁ по двум сторонам и углу между ними. Поэтому OB;\s\up10( –( ^{| |} OB1;\s\up10( –( и ^OB1;\s\up10( –(^ = ^OB;\s\up10( –(^.

О тсюда, с учетом a;\s\up8(( + b;\s\up9(( = OB;\s\up10( –(, вытекает (a;\s\up8(( + b;\s\up9(( ) = OB1;\s\up10( –(. На первом рисунке изображен случай  > 0, а на втором –  < 0. В случае же  = 0, обе части равенства дают o;\s\up8(–(.

Упражнение. Остальные свойства докажите самостоятельно.

Теорема 1 (первый признак коллинеарности векторов). Для того, чтобы ненулевые векторы a;\s\up8(( и b;\s\up9(( были коллинеарны, необходимо и достаточно, чтобы существовало такое число  , что b;\s\up9(( = a;\s\up8((.

Доказательство. Достаточность вытекает непосредственно из определения произведения вектора на число. Если a;\s\up8(( = b;\s\up9((, то по определению a;\s\up8(( ^|| b;\s\up9((.

Необходимость. Пусть a;\s\up8(( ^|| b;\s\up9((.

1 случай: a;\s\up8((  b;\s\up9((. Положим  =b;\s\up9(( _/a;\s\up8(( > 0. Тогда

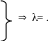a;\s\up8((  a;\s\up8((  a;\s\up8((  b;\s\up9((,

a;\s\up8(( =a;\s\up8(( = ^|a;\s\up8(( ^| = ^|a;\s\up8(( ^| =b;\s\up9((.

2 случай: a;\s\up8((  b;\s\up9((. Положим  = –b;\s\up9(( _/a;\s\up8(( < 0. Тогда

a;\s\up8((  a;\s\up8((  a;\s\up8((  b;\s\up9((,

a;\s\up8(( =a;\s\up8((= –^|a;\s\up8(( ^| = ^|a;\s\up8(( ^| =b;\s\up9((.

Ч то и требовалось доказать.

В процессе доказательства мы показали, как решить следующую задачу: найти вектор b;\s\up9(( сонаправленный с данным вектором a;\s\up8(( и имеющий заданную длину b;\s\up9((= . Это будет вектор b;\s\up9(( = b;\s\up9((. В частности, единичный вектор e;\s\up8(( a;\s\up8(( находится так: e;\s\up8(( = a;\s\up8(( . Такой вектор называется ортом вектора a;\s\up8((.